当克雷数学研究所为七个未解决的数学难题分别设立了100万美元的奖金时,他们可能低估了其中一个条目的价值——而且低估了很多。如果数学家们能够以正确的方式解决计算机科学的“P与NP”问题,其成果的价值可能远远超过100万美元。他们将破解大多数在线安全系统,彻底革新科学,甚至实际上解决所谓的千禧年难题中的其他六个,所有这些难题都是在2000年选定的。无论怎样强调计算机科学中最重要的未解难题的利害关系都不为过,计算机科学就是其中之一。
P与NP问题关注的是寻找问题的解决方案和验证问题的解决方案之间明显的非对称性。例如,假设您正在计划一次世界巡回宣传您的新书。您打开Priceline并开始测试路线,但您尝试的每一条路线都超出了您的旅行预算总额。不幸的是,随着您全球巡演的城市数量增加,要检查的可能路线数量呈指数级增长,即使对于计算机来说,详尽地搜索每种情况也是不可行的。但是当您抱怨时,您的图书经纪人回复了一个航班解决方案序列。您可以通过简单地检查它是否到达每个城市并计算票价与预算限制进行比较,来轻松验证他们的路线是否在预算之内。请注意此处的非对称性:找到解决方案很难,但验证解决方案很容易。
P与NP问题询问这种非对称性是真实的还是幻觉。如果您可以有效地验证问题的解决方案,这是否意味着您也可以有效地找到解决方案?找到解决方案应该比验证解决方案更难,这似乎是显而易见的。但是研究人员以前也感到惊讶。问题看起来可能同样困难,但当您深入挖掘时,您会发现某些问题的捷径,并在其他问题上遇到瓶颈。也许一个巧妙的捷径可以避开图书巡回宣传问题中数万亿条潜在路线的搜索。例如,如果您改为想找到两个特定偏远机场之间且在预算范围内的航班序列,您也可能会对要检查的可能路线数量之多而束手无策。事实上,这个问题包含足够的结构,计算机科学家已经为此开发了一种快速程序(或算法),可以绕过详尽搜索的需求。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和想法的具有影响力的故事的未来。
P与NP问题在我们所看到的计算世界中随处可见,远远超出了我们的旅行场景的具体细节——以至于它已经成为我们理解计算的圣杯的象征。然而,每次尝试解决它都只会进一步揭示证明它是否成立是多么的困难。
在理论计算机科学的子领域,称为复杂性理论,研究人员试图确定计算机可以多么容易地解决各种类型的问题。P代表他们可以有效解决的问题类别,例如在电子表格中对一列数字进行排序或在地图上查找两个地址之间的最短路径。相比之下,NP代表计算机可以有效验证解决方案的问题类别。我们的图书巡回宣传问题,学术界称之为旅行推销员问题,属于NP,因为我们有一个有效的程序来验证代理商的解决方案是否有效。
请注意,NP实际上包含P作为子集,因为彻底解决问题是验证问题解决方案的一种方法。例如,您将如何验证27 × 89 = 2,403?您将自己解决乘法问题并检查您的答案是否与声称的答案匹配。我们通常用简单的维恩图来描述P和NP之间的关系
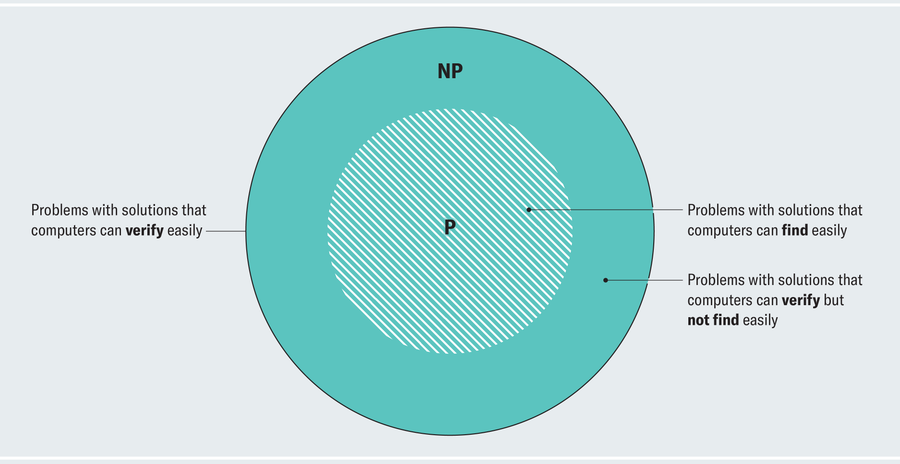
来源:阿曼达·蒙塔内斯
NP内部但不属于P的区域包含无法通过任何已知的有效算法解决的问题。(理论计算机科学家对“有效”使用了可以辩论的技术定义,但它可以作为通俗概念的有用替代。)但我们不知道这是因为此类算法不存在,还是我们只是没有鼓起创造力来发现它们。这种表示法提供了另一种表达P与NP问题的方式:这些类实际上是不同的吗?还是维恩图会坍缩成一个圆圈?所有NP问题都可以有效解决吗?
以下是一些NP中的问题示例,目前尚不清楚它们是否属于P
给定一个社交网络,是否存在一个指定规模的群体,其中所有人都彼此是朋友?
给定各种各样的要运输的箱子,是否可以将它们全部装入指定数量的卡车中?
给定一个数独(推广到 n × n 谜题网格),它是否有解决方案?
给定一张地图,是否可以使用仅三种颜色对国家进行着色,以使没有两个相邻的国家是相同的颜色?
问问自己,您将如何验证对某些列出的问题的建议解决方案,然后您将如何找到解决方案。请注意,近似解决方案或解决小实例(我们大多数人都可以解决9 × 9的数独)是不够的。要符合解决问题的资格,算法需要为所有实例(包括非常大的实例)找到精确的解决方案。
每个问题都可以通过暴力搜索来解决(例如,尝试地图的每种可能的着色,看看是否有任何一种可行),但是要尝试的情况数量随着问题规模的增加呈指数级增长。这意味着,如果我们称问题的规模为 n (例如,地图上的国家数量或要装入卡车的箱子数量),那么要检查的情况数量看起来像 2n。世界上最快的超级计算机也无法对抗指数级增长。即使当 n 等于300时,按照现代数据标准来看,这只是一个很小的输入规模,但 2300 超过了可观测宇宙中原子的数量。在点击此类算法的“开始”按钮后,您的计算机将显示一个旋转的彩色小球,它的寿命将超过您和您的后代。
数千个其他问题也属于我们的列表。从细胞生物学到博弈论,P与NP问题触及科学和工业的遥远角落。如果P = NP(也就是说,我们的维恩图溶解成一个圆圈,并且我们获得了这些看似困难的问题的快速算法),那么整个数字经济将变得容易崩溃。这是因为诸如您的信用卡号和密码之类的许多加密技术通过将私人信息隐藏在计算难度大的问题背后而起作用,只有当您知道密钥时,这些问题才可能变得容易解决。我们所知的在线安全建立在未经证实的数学假设之上,如果P = NP,这些假设就会崩溃。
令人惊讶的是,我们甚至可以将数学本身视为一个NP问题,因为我们可以编程计算机来有效地验证证明。事实上,传奇数学家库尔特·哥德尔在1956年给他的同事约翰·冯·诺伊曼的信中首次提出了P与NP问题。哥德尔观察到P = NP“将产生极其重要的后果。也就是说,这显然意味着……数学家关于是非问题的脑力劳动可以完全被机器取代。”
如果您是一位担心自己工作的数学家,请放心,大多数专家认为P不等于NP。除了有时解决方案应该比验证更难找到的直觉之外,数千个最难的NP问题(目前尚不清楚它们是否属于P)一直未能在不同的领域得到解决,它们闪耀着名誉和财富的诱惑,但还没有人为一个问题设计出有效的算法。
当然,直觉和缺乏反例并不构成证明。要证明P与NP不同,您必须以某种方式排除所有最难的NP问题的潜在算法,这项任务似乎超出了当前数学技术的范围。事实上,该领域通过证明所谓的障碍定理来应对,这些定理表明,解决P与NP问题的所有有希望的证明策略类别都无法成功。我们不仅未能找到证明,而且我们也不知道最终的证明可能是什么样子。
