我通常研究广义相对论和宇宙学。我一直热爱几何事物。小时候,我着迷于地图投影。14岁时,我根据天文学家 E. M. Antoniadi 绘制的火星墨卡托投影平面地图制作了一个彩绘火星地球仪。自从成为普林斯顿大学的荣誉退休教授后,我很高兴地回归到我童年时期的一些兴趣爱好。
我和我的同事 Dave Goldberg 以及 Bob Vanderbei(他发明了用于显示选举结果的“紫色美国”地图)共同制作了我们认为是有史以来最精确的地球平面地图。在平面地图上描绘地球的曲面一直是制图师们几个世纪以来的难题。没有完美的地球平面地图。但平面地图易于存储和制造,因此非常受欢迎。
此前,Goldberg 和我确定了平面地图可能存在的六种关键误差类型:局部形状、面积、距离、屈度(弯曲)、倾斜度(不对称)和边界切口。著名的墨卡托投影,即谷歌地图的基础模板,就说明了这些误差。它具有完美的局部形状,但在描绘面积方面表现不佳。格陵兰岛看起来与南美洲一样大,即使它在全球上的面积仅为南美洲的七分之一。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您将帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的具有影响力的故事。
人们不可能做到尽善尽美。墨卡托地图存在边界切口误差:沿着国际日期变更线的子午线从极点到极点进行 180 度的切割,展开地球表面,从而将夏威夷置于地图的最左侧,将日本置于地图的最右侧,在这个过程中产生了额外的距离误差。飞行员从纽约直飞东京的大圆航线会经过阿拉斯加北部。他的航线在墨卡托地图上看起来是弯曲的——屈度误差。北美洲向北倾斜:加拿大的面积比实际应该的大,而墨西哥则太小。所有这些误差都很重要。忽略其中任何一个都可能导致地图难看,没有人会喜欢。
这里的目标是找到使误差平方和最小化的地图投影——这项技术可以追溯到数学家卡尔·弗里德里希·高斯。墨卡托投影的 Goldberg-Gott 误差评分(六个标准化单项误差项的平方和)为 8.296。分数越低,误差越小,地图越好。地球仪的误差评分为 0.0。我们发现,以前已知的最佳地球平面地图投影是国家地理学会使用的温克尔三投影,其误差评分为 4.563。它具有顶部和底部的直线极线,左右边缘凸出,标记了其在太平洋中部的 180 度边界切口。
我们似乎正在达到改进温克尔三投影的极限。当科学领域出现这种情况时,通常需要突破,一些跳出固有思维模式的想法,才能取得任何根本性的进展。理查德·费曼曾经说过,在物理学中,当我们陷入困境时,当所有旧方法都不奏效时,新的技巧,即将奏效的新方法,将与我们以前见过的任何方法都大相径庭。
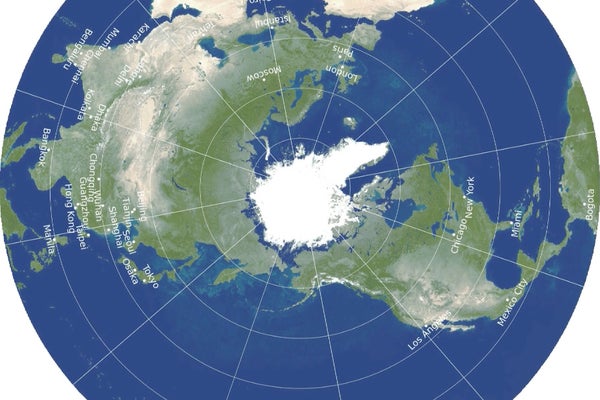
新地图投影的想法来自于我最近撰写的一篇论文《包络多面体》,该论文介绍了一种新型的规则多面体,其中允许多边形背靠背出现。我意识到我可以制作一个背靠背的圆形地图:就像一张老式的唱片。地图的一面显示北半球,另一面显示南半球,赤道环绕边缘。它没有边界切口,并且具有球体的正确拓扑结构。它只是简单地将球体“压扁”。
然后我们必须找到在每一面上绘制特征的最佳公式,该公式将使 Goldberg-Gott 误差评分最小化。答案是北极出现在唱片北侧的中心,经度线从中心向外均匀展开,每条经度线上的比例尺都是均匀的,南侧的情况类似。城市之间的距离通过简单地在它们之间拉一根绳子来测量;如果它们位于相对的半球,绳子只需跨越地图边缘的赤道即可。
新地图的一个缺点是您无法一次看到地球的整个表面,但请记住,地球仪也是如此。在这方面,我们的地图实际上比其他平面地图更像地球仪。要查看地球仪的全部,您必须旋转它;要查看新地图的全部,您只需将其翻过来即可,如下所示
这张双面地图的 Goldberg-Gott 误差评分仅为 0.881,而温克尔三投影为 4.563。它在六个误差项中的每一项都优于温克尔三投影!它具有零边界切口误差,因为大陆和海洋在圆形边缘上是连续的。它具有单面平面地图不具备的显著特性:点对(例如城市)之间的距离误差是有界的,最多仅相差正负 22.2%。在墨卡托投影和温克尔三投影中,距离误差会随着接近极点和边界切口而爆炸式增长。
我们的地图可以从杂志中剪下来,或以活页形式插入杂志中。它们可以用纸板或塑料制成。一个薄盒子可以容纳太阳系所有主要天体的平面双面地图,或者一叠给出物理和政治数据的地球地图。
温克尔三投影是一张可以挂在墙上的地图。我们的地图是一张更精确的,您可以拿在手中的地图。
这是一篇观点和分析文章。