当你点击短信上的“发送”键时,很容易想象这条信息会直接从你的手机传到你朋友的手机上。但事实上,它通常会经过蜂窝网络或互联网的长途跋涉,而这两种网络都依赖于集中的基础设施,这些基础设施可能会因自然灾害而受损,或被压迫性政府关闭。出于对国家监视或干预的担忧,香港精通技术的抗议者避开了互联网,转而使用 FireChat 和 Bridgefy 等软件,在附近的手机之间直接发送消息。
这些应用程序可以让信息在手机之间静默跳跃,最终将发送者与接收者连接起来——只有用户才能查看消息。这种链接手机的集合,被称为网状网络或移动自组网,实现了一种灵活和去中心化的通信模式。但是,为了让任何两部手机进行通信,它们需要通过一系列其他手机连接起来。在香港各地分散的人群中,有多少人需要通过同一个网状网络连接,我们才能确信可以实现跨城通信?

图片来源:Jen Christiansen(图表);Wee People 字体,ProPublica 和 Alberto Cairo(人物绘图)
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够继续产出关于塑造我们当今世界的发现和想法的有影响力的报道。
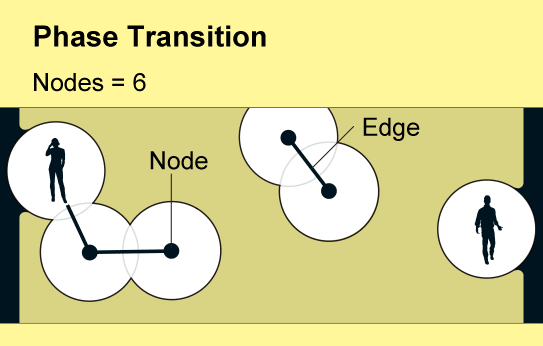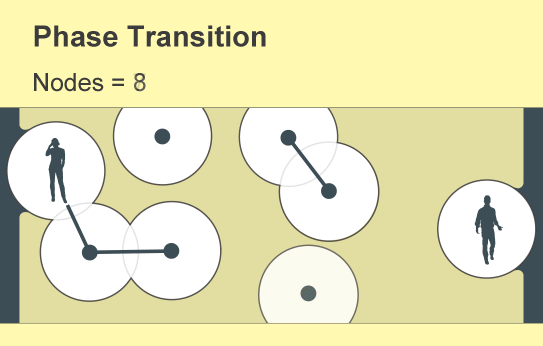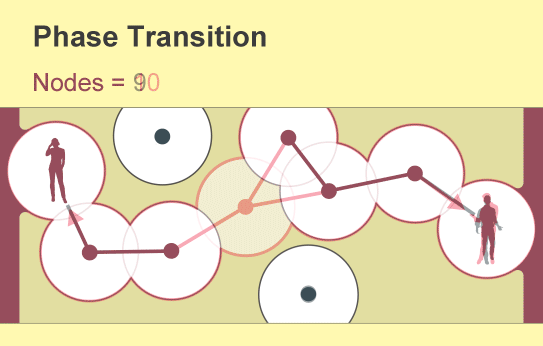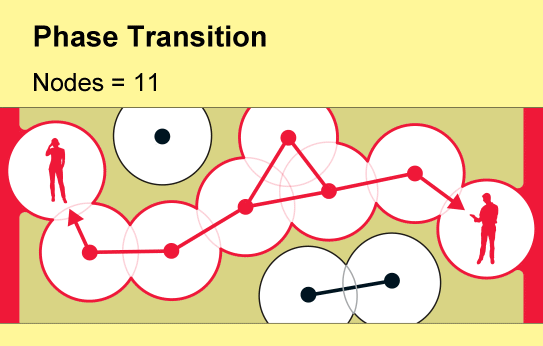
一个名为渗流理论的数学分支提供了一个令人惊讶的答案:仅仅少数人就可以产生巨大的影响。当用户加入新网络时,孤立的连接手机群会慢慢出现。但是,当用户密度超过一个临界且急剧的阈值时,东西或南北方向的完全通信就会突然出现。科学家将网络连通性的这种快速变化描述为相变——这个概念也用于解释材料状态的突然变化,例如冰的融化或水的沸腾。
图片来源:Jen Christiansen(图表);Wee People 字体,ProPublica 和 Alberto Cairo(人物绘图)
渗流理论研究在网络中随机创建或移除链接的后果,数学家将网络概念化为节点(用点表示)与“边”(线)的集合。每个节点代表一个对象,例如手机或人,边代表它们两者之间的特定关系。渗流理论的基本见解可以追溯到 20 世纪 50 年代,即随着网络中链接数量的逐渐增加,一个全球互联的节点集群将突然出现。
科学家们努力回答的问题是:何时?对于任何给定的网络,相当于冰融化的零摄氏度或水沸腾的 100 摄氏度是什么?一个模因在何时会走红?一种产品在何时会主导市场?地震在何时开始?手机网络在何时实现完全连接?或者疾病在何时变成全球大流行?渗流理论为所有这些转变提供了深刻的见解。
数学家通常研究理想化的网络——几何对称且无限延伸——因为这些网络适合理论计算。无限网络通常是唯一具有真正急剧相变的网络。现实世界的网络范围有限,通常很混乱,并且需要具有挑战性的计算——但是它们也具有转变,尽管转变更为平缓。随着世界通过复杂链接层变得日益互联,这些链接层传输人员,通过电网为他们提供能源,或通过社交媒体将他们连接起来——有时还在他们之间传播疾病——渗流理论变得越来越相关。
突然到位
1957 年,英国数学家西蒙·拉尔夫·布罗德本特和约翰·迈克尔·哈默斯利首次将渗流理论定义为一个纯粹的数学问题。他们从化学中抽象出对渗流的研究,化学描述了流体过滤通过材料的过程,例如石油渗过多孔岩石或水过滤过研磨咖啡。岩层渗流网络由其结构中的小孔组成,表示为节点,以及允许流体在它们之间流动的通道或裂缝,表示为边。毫不奇怪,石油在裂缝更多的岩石中流动得更远。布罗德本特和哈默斯利使用渗流理论预测,在理想化的岩石中,当裂缝密度超过某个阈值时,石油将从仅在小区域流动转变为突然渗透几乎整个岩石。
地质学家使用渗流理论的一个版本来研究裂缝岩石中簇的大小,这与通过水力压裂法提取石油和地震的发生有关。为了模拟地震,地震学家创建了与观测到的裂缝尺度和密度相匹配的渗流网络,然后通过调整裂缝连接起来的概率来考虑应力。随着应力和链接的增加,簇会扩展,直到突然且不可预测地爆发地震。渗流过程的修改版本允许裂缝愈合和再次断裂,以模拟余震或长期变化。
渗流理论还阐明了更小尺度上的物理和化学过程,例如聚合,即称为单体的小而简单的分子结合在一起形成称为聚合物的较大簇的过程。在渗流理论框架中,每个单体充当一个节点,两个相邻单体可能自发形成一个键或边。如果它们连接的可能性增加,系统最终将达到渗流阈值,并且将出现一个巨大的、连接的聚合物。这个过程就是导致溶于水的明胶粉末凝固并形成果冻的原因。
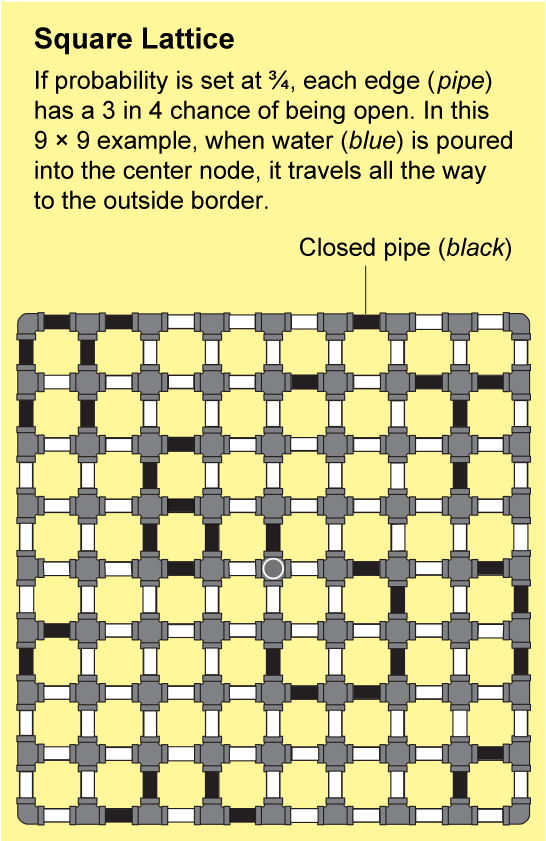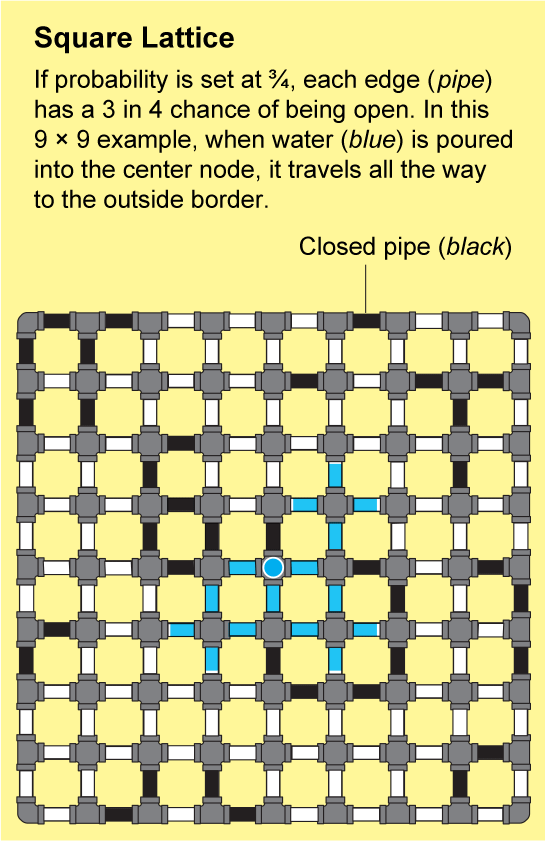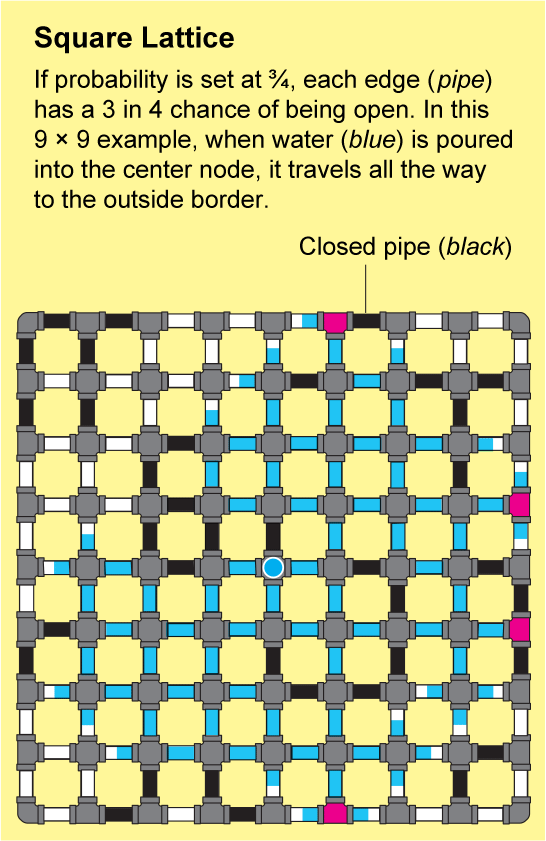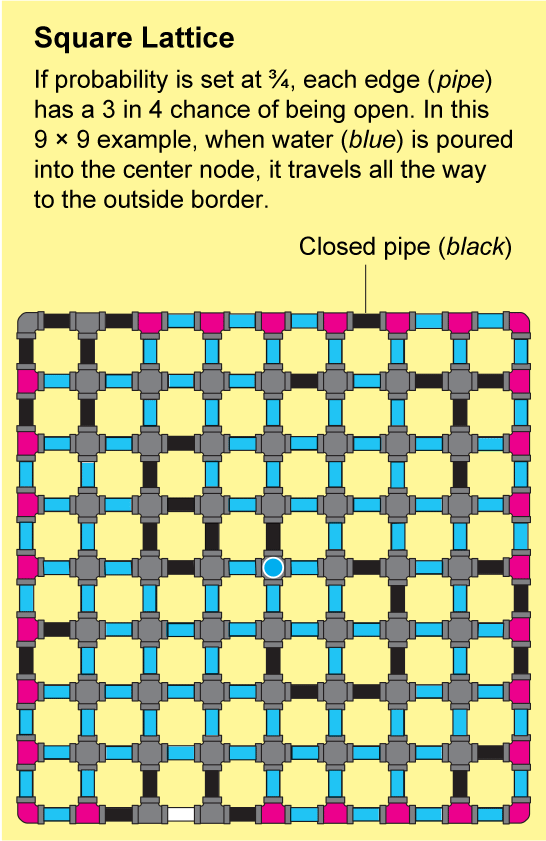
裂缝岩石或连接聚合物中的网络非常复杂。几乎不可能精确地描述它们的结构,但是布罗德本特和哈默斯利表明,它们可以用易于分析的重复模式来近似。最简单的例子是正方晶格,它看起来像一张无尽的方格纸:节点排列成网格,并通过四条边连接到它们的邻居。
为了了解流体如何在晶格中传播,假设方格纸上的每条小边都是一根管道,管道要么打开,要么关闭。我们可以通过抛掷一面标有“打开”和另一面标有“关闭”的硬币来确定每根管道的状态。由此产生的打开和关闭管道的景观将是一个随机网络,并且它将具有一些“打开”的簇,其中所有节点都通过一系列打开的管道连接。如果你将水倒入这样一个簇中的任何节点,水将通过打开的管道流到该簇中的所有其他节点。
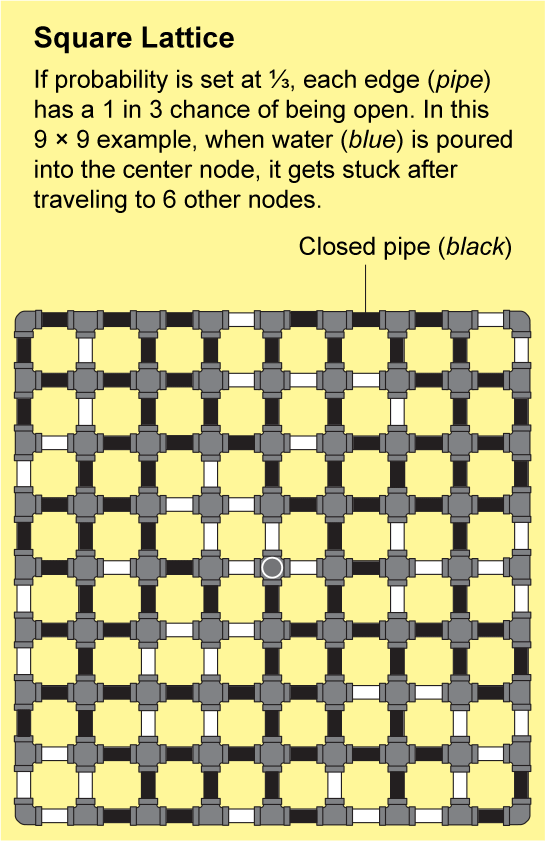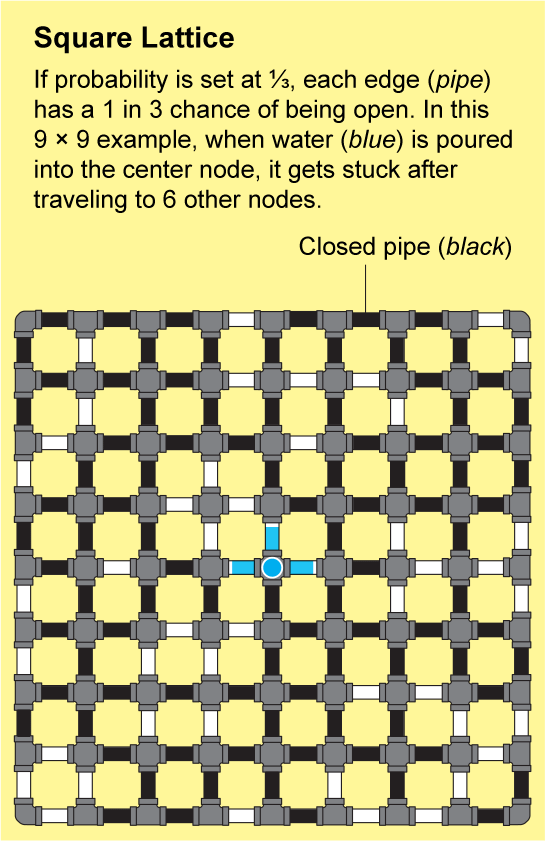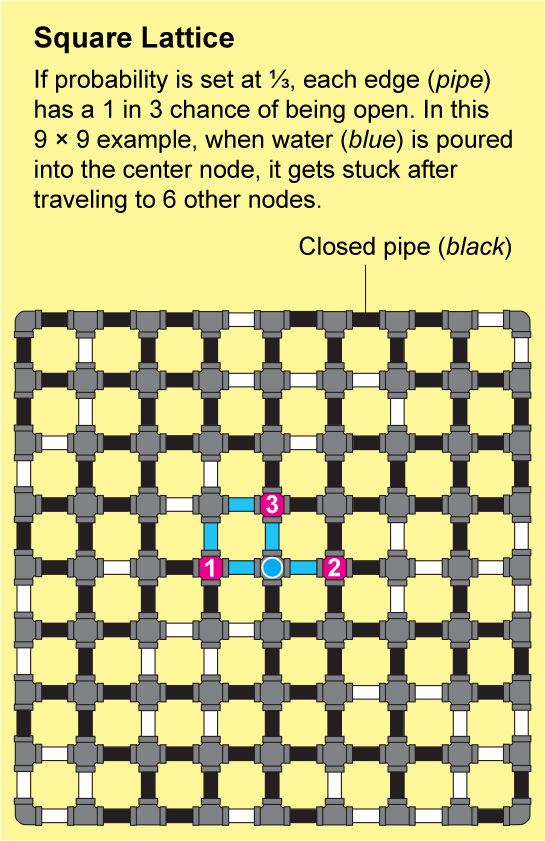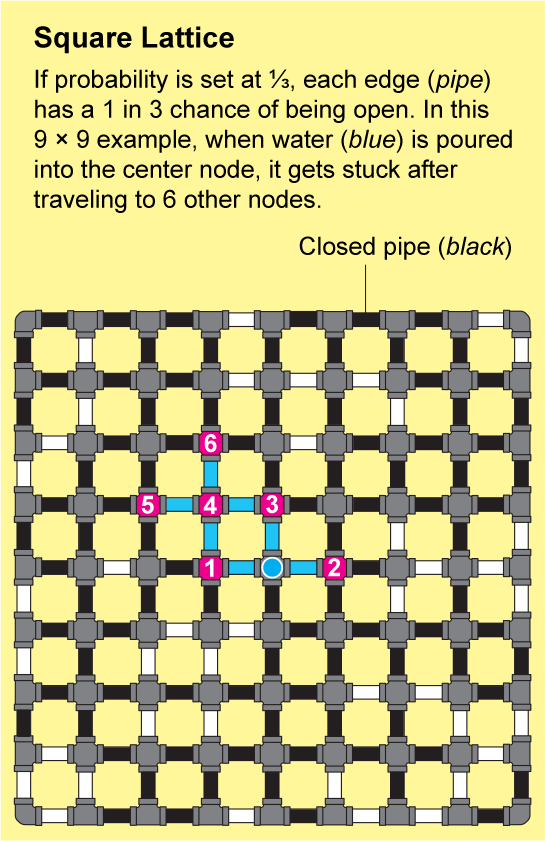
图片来源:Jen Christiansen
图片来源:Jen Christiansen
渗流理论关注网络的连通性,这对应于打开的簇有多大。“大”是一个模糊的概念,不容易进行数学形式化。因此,数学家经常用无穷大代替大数。因此,中心问题变成了:是否存在无限簇?“对我们来说,回答这个是或否的问题比回答我们看到了多少个这种或那种大小的大簇要容易得多,”柏林魏尔斯特拉斯应用分析与随机研究所的数学家贝内迪克特·亚内尔说。
事实上,无限网络具有无限簇的可能性总是 0 或 100%。这是因为渗流过程受概率论中的一个普遍原则支配,即零一律,由俄罗斯数学家安德烈·柯尔莫哥洛夫在 20 世纪 30 年代发现。假设你无限次地抛掷一枚硬币。零一律适用于任何关于结果的问题,其答案不依赖于任何有限次数的抛掷。(例如,对于问题“你抛掷出正面无限多次了吗?”的答案,如果你改变有限次数的抛掷,答案不会改变,但是对于问题“你在第三次抛掷中抛掷出正面了吗?”的答案,可以通过仅改变一次抛掷来改变。)
零一律告诉我们,有限的变化不会扰乱无限性质的现象。因此,在无限网络中找到无限簇的概率不能稍微改变,例如从 0.81 变为 0.82;它必须采取极端位置之一——零或一。换句话说,无限网络要么没有无限簇(找到无限簇的概率为零),要么有无限簇(概率为一)。
因此,将有限数量的打开管道切换为关闭管道,反之亦然,对是否存在无限打开簇没有任何影响。找到无限簇的概率要么是零,要么是一。是哪个呢?
找到阈值
答案取决于你的硬币的偏差。想象你有一个控制偏差的拨盘。当拨盘完全向左转动时,硬币将始终落在“关闭”面上。一旦所有管道都关闭,倒入节点的水将不会流到任何地方,并且找到无限簇的概率将为零。当你顺时针转动拨盘时,硬币落在“打开”面上的概率会增加,并且随着额外的抛掷,将会有越来越多的打开管道。当拨盘完全向右转动时,硬币将始终落在“打开”面上,最终倒入一个节点的水将流到其他所有地方。然后,找到无限簇的概率为一。
如果你缓慢地顺时针转动拨盘,管道打开的可能性会逐渐增加,并且似乎找到无限簇的机会也应该从零逐渐增加到一。事实上,由于零一律,变化会瞬间发生:它表明可能性不能介于零和一之间。对于正方晶格,当拨盘正好在中间时——当硬币没有偏差时,概率会从零突变为一。拨盘的这个临界位置被称为渗流阈值。无论网络的形状如何——例如,它是三角晶格还是正方晶格的三维版本——渗流理论的本质问题仍然相同:阈值在哪里?在保证有足够的链接打开以保证无限打开簇之前,硬币需要有多大的偏差?
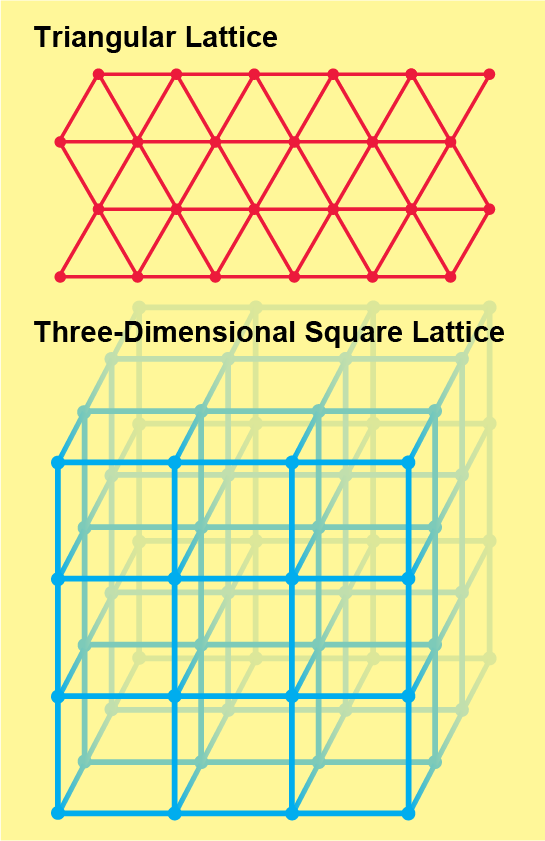
图片来源:Jen Christiansen
答案取决于(无限)网络的精确形状,并且远非易于找到。即使证明正方晶格——最简单的系统——的阈值为二分之一也是一个艰巨的挑战,数学家哈里·克斯顿在 1980 年最终解决了这个问题。尽管经过数十年的努力,但精确的渗流阈值仅对少数极其简单的网络是已知的。“仅仅为了找到阈值就做了大量的工作,”密歇根大学的统计物理学家罗伯特·M·齐夫说。“人们研究了多少不同的系统,真是令人难以置信。”齐夫整理了一个维基百科页面,记录了数百个不同网络的渗流阈值。三角晶格的偏差约为 0.347,这个数字是通过分析确定的,但该页面上的绝大多数数字(包括三维正方晶格的阈值偏差)都是通过计算机模拟得出的近似值。
网状网络
晶格是物理系统中渗流的良好模型,例如裂缝岩石,其中孔洞的位置是固定的,并且它们之间的裂缝随机形成。但是,其他现实世界的网络要复杂得多。例如,在前面提到的 FireChat 和 Bridgefy 网状网络中,节点的位置——香港抗议者携带的手机——不断变化。当两部手机彼此足够靠近时——在用于共享消息的基于蓝牙的应用程序的数十米范围内,网络中的边或连接就会形成。这种网络由不同的模型描述,称为连续渗流,因为网状网络的节点可以位于连续空间中的任何位置。
像任何数学模型一样,这个网络的抽象版本基于简化的假设。智能手机是随机分散的,没有模仿人们蜿蜒路线图中的自然簇和模式,并且两部智能手机仅根据它们之间的距离连接,而没有考虑墙壁或其他干扰。尽管如此,该模型仍然突出了渗流理论在真实网状网络中发挥的核心作用。
有两种方法可以提高这种连续渗流网络的连通性:启用更长范围的直接连接或添加更多智能手机,从而增加用户密度。这些修改可以被认为是像管道网络中描述的那些拨盘;顺时针转动任何一个拨盘都会增加连通性。并且在这些模型中,“存在一个开关,你真的可以从局部连通性转变为全局连通性,”亚内尔说。
对于网状网络应用程序的设计者来说,找到渗流阈值是一个实际的工程问题。更改设备的功率(控制范围)是转动拨盘的一种方式。网状网络公司 goTenna 的首席科学家拉姆·拉马纳坦说,中心问题是,“你希望发射功率是多少才能拥有一个连接的网络?”如果功率和连通性具有线性关系——如果功率的每次小幅增加都导致连通性的成比例小幅增加,那么答案将非常简单。但是渗流阈值的存在意味着存在网络会随着人们的移动而突然失去连通性的风险。最佳功率是既能确保网络始终连接又不会浪费能量的功率。
另一个拨盘是手机的密度。具有固定范围的网状网络需要临界用户密度,并且最有可能在拥挤的活动(例如音乐节、足球比赛或大型抗议活动)中提供广泛的连通性。Bridgefy 的首席执行官兼联合创始人豪尔赫·里奥斯说,该公司看到在克什米尔、尼日利亚、香港和伊朗的内乱时期,新用户大幅增加,当时人们转向网状网络,以便在政府关闭互联网或大量人群阻塞蜂窝连接时保持通信。纽约布鲁克林的红钩区等一些社区正在使用网状网络,通过将永久节点固定在建筑物顶部来扩展互联网接入。许多必要的硬件和路由技术仍在发展中,但很容易想象大胆的、未来的应用——例如,自动驾驶汽车可以直接通信,共享关于交通模式或道路危险的信息,而无需依赖任何额外的基础设施。
疾病接触网络
用于模拟石油在岩石中流动或手机之间直接通信的网络模仿了这些系统的真实空间结构:如果它们代表的对象在物理空间中彼此靠近,则两个节点通过一条边连接。但是,对于跟踪疾病在人与人之间传播的网络,链接由特定病菌在他们之间传播的方式决定。这种网络特别复杂:一个受感染的人在大城市的一家夜总会里待了一个小时,可能会将病毒传播给一个人,这个人会在接下来的几天里将病毒带到全国甚至跨越大陆。
最简单的流行病学模型将每个人分为三类——易感人群、感染人群和康复人群——并忽略了这种复杂的连接结构。在这样的模型中,感染者在假设该组中的每个人——宿舍里的学生或城市居民——同样容易感染的情况下,将疾病传播给易感人群中的随机其他人。易感人群被感染的速度取决于基本再生数,即单个感染者引起的平均新感染数,缩写为 R0。如果 R0 大于 1,则病毒正在传播,如果小于 1,则疫情正在消退。
然而,在实践中,人们彼此之间的互动方式会影响疾病的整体传播。例如,2003 年爆发的严重急性呼吸综合征(SARS)最初的 R0 值介于 2.2 和 3.6 之间,但病例数“远低于此期间的预期,正如一个简单的计算所表明的那样,”劳伦·安塞尔·迈耶斯写道,她现在是德克萨斯大学 COVID-19 建模联盟的主任,她在2006 年的一篇文章中写道。她认为,这种差异源于“所有易感个体都同样容易被感染”的假设,该假设忽略了人们接触网络的复杂形状。特别是,SARS 的估计 R0 值是基于其在公寓楼和医院中的快速传播,与普通人群相比,这些场所“个体之间的密切接触率异常高”。但是,由于感染 SARS 的人很快就会病得很重,因此他们在医院中结束治疗,然后才可能感染医院外面的许多人。
疾病网络中的边表示特定的关系。例如,在显示 HIV 潜在传播的网络中,如果两个人交换了体液,则他们通过一条边连接。显示 COVID-19 潜在传播的网络具有非常不同的边结构,表示在没有呼吸防护的情况下进行密切接触。封锁或限制,例如关闭企业和限制旅行,会改变这种边结构,并与口罩和身体疏远一起,阻止病毒从一个人或节点传播到另一个人或节点。流行病学家面临的一个挑战是找到充分断开网络连接的方法。
现实世界中的疾病接触网络,例如显示 COVID-19 传播的网络,极其复杂且难以精确描述。即使网络的精确结构是已知的,在数学上分析它也将具有挑战性。计算机模拟和海量数据分析被用于预测未来的病例数,评估一米与两米社交距离的影响,并量化学校和餐馆在冠状病毒传播中的重要性。东北大学的复杂网络理论家亚历山德罗·韦斯皮尼亚尼将这项研究称为他的“战时”工作——战术性的,偶尔也很混乱,但产生了决策者和医护人员需要的直接的数字结果。韦斯皮尼亚尼和他的同事创建了“一种合成社会,其中所有这些个体都被打包到一台计算机中”以运行模拟,他说。
相比之下,韦斯皮尼亚尼将他的“和平时期”研究称为“你开发模型,你校准不同的建模事物方式,你开发特定的方法,你研究如何改进你的结果”的时期。为了获得对网络的基本形状和结构特征如何影响疾病传播的理论理解,科学家们转向了渗流理论。
传统的纸笔渗流数学工具仅在最简单的情况下才有效,在这些情况下,网络是人为有序和对称的。即便如此,“数学对于指导你的理解至关重要,”韦斯皮尼亚尼说。网络流行病学家将网络简化为最基本要素,特别是其所谓的度分布。度是特定节点连接到的其他节点的数量。例如,在正方晶格中,所有节点的度均为 4。然而,在疾病网络中,度数差异很大:有些人有很多接触,并且可能将疾病传播给很多人,而另一些人则相当孤立。
度分布描述了节点具有每个度的可能性。在疾病接触网络中,这转化为某人感染(或可能被感染)一定数量的其他人的可能性。为了理解这个方面如何影响渗流阈值,像迈耶斯这样的数学流行病学家生成了数千个样本网络,这些网络本质上是随机的,但只有一个特征:它们都具有相同的度分布。这种方法是一种分离度分布的方式,以感知其在网络结构中的作用。如果生成的网络的属性与真实世界的网络相匹配,那么“融入数学的”度分布或任何其他特征可能与疾病的传播相关,迈耶斯说。如果匹配是完美的,“那么你的数学结果将看起来就像你的模拟。”
研究表明,如果网络具有更广泛的度分布,即节点度数的范围更广,则网络的渗流阈值会降低。因此,在具有一些高度连接的人和一些孤立个体的网络中,疾病比在每个人都具有大致相同接触次数的网络中更容易传播。澳大利亚墨尔本拉筹伯大学的数学流行病学家乔尔·米勒启发式地解释了这种观察:“如果我的接触次数是你的 10 倍,那么我被感染的可能性是你的 10 倍,我传播的可能性也是你的 10 倍,因此这对于疾病传播的重要性是 100 倍。”
未来的网络
渗流理论被用于模拟其他“传染”现象,例如社交媒体网络上的模因在突然走红之前缓慢获得关注的情况。它可以应用于经济模型,以展示当人们在社交联系人之间分享推荐时,特定产品如何迅速占据市场主导地位。选民模型(人们影响其社区)也显示出阈值效应。
与数学家传统上研究的无限的、整齐有序的网络相反,从真实示例中派生的网络在范围上是有限的且混乱的。有限网络不会像无限网络那样立即从在小范围内连接跳跃到几乎在所有地方都连接,但它们通常确实会非常快速地进行切换。为了理解这些过程,网络理论家在数学和计算机模拟之间来回切换。更简单的网络指导他们构建实际网络的详细计算机模型,从中吸取的教训反过来又影响了他们如何修改纸笔模型,以深入了解现实世界。
COVID-19 传播的许多重要网络模型都集成了来自其他网络的信息。学校系统、火车路线和医院员工时间表都形成了网络——并且每个网络都会影响疫情的进程。“我们生活在这个相互依存的网络系统中,我们不能只考虑一个网络而不了解其他网络带来的后果,”加州大学戴维斯分校的复杂网络理论家拉伊萨·德索萨说。每个网络都是其自身的复杂系统,具有其自身的涌现行为。我们越来越多地将这些网络耦合起来,以创建一个更加复杂的系统。但是,没有明确的理论框架来研究这种网络网络。理解它们的属性如何受到组成网络的属性的影响是未来的一个挑战。
“我们不是生活在一个泡沫中或一个完全混合的世界中。我们生活在一个有联系的世界中,我们关注 Twitter 帐户,而这些是渗流和其他模型进入的地方,”韦斯皮尼亚尼说。现在更好地理解这些理论数学模型“可以在未来发挥作用”。渗流网络易于适应,为数学家提供了新的游乐场,为科学家提供了实际应用,但这些多样化的模型由一个令人惊讶的特征统一起来:它们都具有一个急剧的支点,只需几个新的连接就可以将网络连接在一起。随着世界变得越来越互联,理解这些关键转变的必要性变得越来越迫切。

