我们都曾有过因试图设置密码,却被告知密码太弱而感到沮丧的经历。我们也经常被告知要定期更改密码。显然,这些措施增加了安全性,但究竟是如何增加的呢?
我将解释一些标准建议背后的数学原理,包括阐明为什么六个字符不足以构成一个好的密码,以及为什么您永远不应该只使用小写字母。我还将解释黑客如何在被盗数据集中即使没有密码也能破解密码。
明智地选择密码#W!sely@*
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将帮助确保未来能够继续发布关于塑造当今世界的发现和思想的具有影响力的报道。
以下是设置防黑客密码背后的逻辑。当您被要求创建一个具有特定长度和元素组合的密码时,您的选择将符合符合该规则的所有唯一选项的范围——即“可能性空间”。例如,如果您被告知使用六个小写字母——例如,afzjxd、auntie、secret、wwwwww——则空间将包含 266,即 308,915,776 种可能性。换句话说,第一个字母有 26 种可能的选择,第二个字母有 26 种可能的选择,依此类推。这些选择是独立的:您不必使用不同的字母,因此密码空间的大小是可能性的乘积,即 26 x 26 x 26 x 26 x 26 x 26 = 266。
如果您被告知选择一个 12 个字符的密码,该密码可以包含大写和小写字母、10 个数字和 10 个符号(例如,!、@、#、$、%、^、&、?、/ 和 +),则密码的 12 个字符中的每一个字符将有 72 种可能性。可能性空间的大小将为 7212 (19,408,409,961,765,342,806,016,或接近 19 x 1021)。
这比第一个空间大 62 万亿倍以上。一台计算机逐个遍历您的 12 个字符密码的所有可能性,将花费 62 万亿倍的时间。如果您的计算机花费一秒钟访问六个字符的空间,那么它将不得不花费两百万年的时间来检查 12 个字符空间中的每个密码。大量的可能性使得黑客难以实施对于六个字符空间来说可能可行的攻击计划。
通过计算机计算这些空间的大小通常涉及计算可能性数量中的二进制位数。该数字 N 来自以下公式:1 + integer(log2(N))。在该公式中,log2(N) 的值是一个带有许多小数位的实数,例如 log2(266) = 28.202638…。公式中的“integer”表示省略该对数值的小数部分,向下舍入为整数——如 integer(28.202638… 28)。对于上面六个小写字母的示例,计算结果为 29 位;对于更复杂的 12 个字符的示例,计算结果为 75 位。(数学家将可能性空间分别称为具有 29 位和 75 位的熵。)法国国家网络安全机构 (ANSSI) 建议,当涉及到密码或绝对必须安全的加密系统的密钥时,空间应至少具有 100 位。加密涉及以一种方式表示数据,以确保除非接收者拥有秘密的破译密钥,否则无法检索数据。事实上,该机构建议可能性空间为 128 位,以保证未来几年的安全性。它认为 64 位非常小(非常弱);64 到 80 位小;80 到 100 位中等(中等强度)。
摩尔定律(该定律指出,在一定价格下可用的计算机处理能力大约每两年翻一番)解释了为什么相对较弱的密码不足以长期使用:随着时间的推移,使用蛮力的计算机可以更快地找到密码。尽管摩尔定律的速度似乎正在下降,但对于您希望长期保持安全的密码,明智的做法是将其考虑在内。
对于 ANSSI 定义的真正强大的密码,您将需要,例如,一个由 16 个字符组成的序列,每个字符取自一组 200 个字符。这将构成一个 123 位的空间,这将使密码几乎不可能记住。因此,系统设计人员通常要求较低,并接受低强度或中等强度的密码。只有当密码由系统自动生成,且用户不必记住密码时,他们才会坚持使用长密码。
还有其他方法可以防止密码破解。最简单的方法是信用卡常用的众所周知的方法:在三次尝试失败后,访问将被阻止。还提出了其他替代想法,例如在每次连续尝试失败后将等待时间加倍,但允许系统在一段较长时间(例如 24 小时)后重置。然而,当攻击者能够在未被检测到的情况下访问系统,或者如果系统无法配置为中断和禁用失败的尝试时,这些方法是无效的。
.jpg?w=900)
搜索所有可能的密码需要多长时间?
为了使密码难以破解,应从大量的可能性集合或“空间”中随机选择密码。可能性空间的大小 T 取决于密码中有效字符列表的长度 A 和密码中的字符数 N。这个空间的大小 (T = AN) 可能差异很大。
以下每个示例都指定了 A、N、T 的值以及黑客必须花费的时间 D(小时),才能逐个尝试每个字符排列。 X 是在假设摩尔定律(计算能力每两年翻一番)仍然有效的情况下,空间可以在不到一小时内检查完毕之前必须经过的年数。我还假设在 2019 年,一台计算机每秒可以探索十亿种可能性。我用以下三个关系式表示这组假设,并考虑基于 A 和 N: 值的五种可能性
关系式
T = AN
D = T/(109 × 3,600)
X = 2 log2[T/(109 × 3,600)]
结果
_________________________________
如果 A = 26 且 N = 6,则 T = 308,915,776
D = 0.0000858 计算小时
X = 0;已经可以在一小时内破解该空间中的所有密码
_________________________________
如果 A = 26 且 N = 12,则 T = 9.5 × 1016
D = 26,508 计算小时
X = 29 年后密码可以在一小时内被破解
_________________________________
如果 A = 100 且 N = 10,则 T = 1020
D = 27,777,777 计算小时
X = 49 年后密码可以在一小时内被破解
_________________________________
如果 A = 100 且 N = 15,则 T = 1030
D = 2.7 × 1017 计算小时
X = 115 年后密码可以在一小时内被破解
________________________________
如果 A = 200 且 N = 20,则 T = 1.05 × 1046
D = 2.7 × 1033 计算小时
X = 222 年后密码可以在一小时内被破解
武器化字典和其他黑客技巧
攻击者通常会成功从系统中获取加密密码或密码“指纹”(稍后我将更全面地讨论)。如果黑客攻击未被检测到,入侵者可能有几天甚至几周的时间来尝试推导出实际密码。
为了理解在这种情况下利用的微妙过程,请再次审视可能性空间。当我之前谈到位大小和密码空间(或熵)时,我隐含地假设用户始终随机选择密码。但通常选择不是随机的:人们倾向于选择他们可以记住的密码(locomotive),而不是任意的字符字符串(xdichqewax)。
这种做法对安全性构成严重问题,因为它使密码容易受到所谓的字典攻击。常用的密码列表已被收集并根据其使用频率进行分类。攻击者通过系统地浏览这些列表来尝试破解密码。这种方法非常有效,因为在没有具体约束的情况下,人们自然会选择简单的单词、姓氏、名字和简短的句子,这大大限制了可能性。换句话说,密码的非随机选择本质上缩小了可能性空间,从而减少了解开密码所需的平均尝试次数。
以下是其中一个密码字典中的前 25 个条目,按顺序列出,从最常见的密码开始。(我从 2017 年泄露并由 SplashData 分析的 500 万个密码的数据库中提取了示例。)
1. 123456
2. password
3. 12345678
4. qwerty
5. 12345
6. 123456789
7. letmein
8. 1234567
9. football
10. iloveyou
11. admin
12. welcome
13. monkey
14. login
15. abc123
16. starwars
17. 123123
18. dragon
19. passw0rd
20. master
21. hello
22. freedom
23. whatever
24. qazwsx
25. trustno1
如果您使用 password 或 iloveyou,您并没有您想象的那么聪明!当然,列表会因收集列表的国家和所涉及的网站而异;它们也会随着时间而变化。
对于四位数字密码(例如,智能手机上 SIM 卡的 PIN 码),结果更缺乏想象力。2013 年,根据 DataGenetics 网站收集的 340 万个每个包含四位数字的密码,最常用的四位数字序列(占选择的 11%)是 1234,其次是 1111(6%)和 0000(2%)。最少使用的四位数字密码是 8068。不过,请注意,由于结果已发布,此排名可能不再真实。在数据库中的 340 万个四位数字序列中,8068 这个选择仅出现 25 次,远低于如果每个四位数字组合的使用频率相同,则应出现的 340 次使用。前 20 个四位数字系列是:1234;1111;0000;1212;7777;1004;2000;4444;2222;6969;9999;3333;5555;6666;1122;1313;8888;4321;2001;1010。
即使没有密码字典,使用语言中字母使用频率(或双字母)的差异也可以计划有效的攻击。一些攻击方法还考虑到,为了方便记忆,人们可能会选择具有特定结构的密码——例如 A1=B2=C3、AwX2AwX2 或 O0o.lli.(我长期使用)——或者通过组合几个简单的字符串来派生密码,例如 password123 或 johnABC0000。利用这些规律性可以使黑客加快检测速度。
哈希黑客
正如正文解释的那样,互联网服务器不存储客户端的密码,而是存储这些密码的“指纹”:从密码派生的字符序列。在发生攻击时,使用指纹可以使黑客很难(如果不是不可能)使用他们发现的内容。
这种转换是通过使用称为加密哈希函数的算法来实现的。这些是精心开发的过程,可以将数据文件 F(无论其长度如何)转换为序列 h(F),称为 F 的指纹。例如,哈希函数 SHA256 将短语“Nice weather”转换为
DB0436DB78280F3B45C2E09654522197D59EC98E7E64AEB967A2A19EF7C394A3
(64 个十六进制或 16 进制字符,相当于 256 位)
更改文件中的单个字符会完全改变其指纹。例如,如果 Nice weather 的第一个字符更改为小写 (nice weather),则哈希 SHA256 将生成另一个指纹
02C532E7418CD1B57961A1B090DB6EC37B3C58380AC0E6877F3B6155C974647E
您可以自己进行这些计算并在 https://passwordsgenerator.net/sha256-hash-generator 或 www.xorbin.com/tools/sha256-hash-calculator 上查看它们
良好的哈希函数生成的指纹类似于如果均匀随机选择指纹序列所获得的指纹。特别是,对于任何可能的随机结果(64 个十六进制字符的序列),在合理的时间内不可能找到具有此指纹的数据文件 F。
哈希函数已经经历了几个发展阶段。SHA0 和 SHA1 世代已经过时,不建议使用。包括 SHA256 在内的 SHA2 世代被认为是安全的。
给消费者的启示
考虑到所有这些,设计良好的网站会在创建密码时分析用户提出的密码,并拒绝那些太容易恢复的密码。这很烦人,但为了您好。
对于用户来说,显而易见的结论是他们必须随机选择密码。一些软件确实提供了随机密码。但是,请注意,此类密码生成软件可能有意或无意地使用不良的伪随机生成器,在这种情况下,它提供的密码可能并不完美。
您可以使用名为 Pwned Passwords (https://haveibeenpwned.com/Passwords) 的 Web 工具检查您的任何密码是否已被黑客入侵。其数据库包含超过 5 亿个在各种攻击后获得的密码。
我尝试了 e=mc2e=mc2,我喜欢这个密码并认为它很安全,但收到了令人不安的回复:“此密码之前已被看到 114 次。” 其他尝试表明,很难想出数据库不知道的易于记忆的密码。例如,aaaaaa 出现了 395,299 次;a1b2c3d4 出现了 113,550 次;abcdcba 出现了 378 次;abczyx 出现了 186 次;acegi 出现了 117 次;clinton 出现了 18,869 次;bush 出现了 3,291 次;obama 出现了 2,391 次;trump 出现了 859 次。
仍然有可能保持原创性。例如,该网站无法识别以下六个密码:eyahaled(我的名字倒过来拼写);bizzzzard;meaudepace 和 modeuxpass(法语“密码”的两个双关语);abcdef2019;passwaurde。既然我已经尝试过它们,我想知道数据库下次更新时是否会添加它们。如果是这样,我就不会使用它们了。
给网站的建议
网站也遵循各种经验法则。美国国家标准与技术研究院最近发布了一份通知,建议使用字典来过滤用户的密码选择。
优秀的 Web 服务器设计人员绝对必须遵守的规则之一是,不要将用户名和密码的明文列表存储在用于运行网站的计算机上。
原因很明显:黑客可能会访问包含此列表的计算机,原因可能是该站点保护不力,或者系统或处理器包含除攻击者外无人知晓的严重缺陷(所谓的零日漏洞),攻击者可以利用该漏洞。
一种替代方法是在服务器上加密密码:使用秘密代码,通过加密密钥将密码转换为对于任何没有解密密钥的人来说都像是随机字符序列的内容。这种方法有效,但有两个缺点。首先,每次将其与用户条目进行比较时,都需要解密存储的密码,这很不方便。其次,更严重的是,这种比较所需的解密需要在网站计算机的内存中存储解密密钥。因此,攻击者可能会检测到此密钥,这使我们回到了最初的问题。
存储密码的更好方法是通过称为哈希函数的方法,该方法生成“指纹”。对于文件中的任何数据(符号化为 F),哈希函数都会生成指纹。(该过程也称为压缩或哈希。)指纹 h(F) 是与 F 关联的相当短的单词,但以一种方式生成,实际上,不可能从 h(F) 推导出 F。哈希函数被称为单向的:从 F 到 h(F) 很容易;从 h(F) 到 F 实际上是不可能的。此外,使用的哈希函数具有以下特性:即使两个数据输入 F 和 F' 可能具有相同的指纹(称为冲突),但在实践中,对于给定的 F,几乎不可能找到指纹与 F 相同的 F'。
使用此类哈希函数可以将密码安全地存储在计算机上。服务器不存储配对的用户名和密码列表,而是仅存储用户名/指纹对列表。
当用户希望连接时,服务器将读取个人的密码,计算指纹,并确定它是否与与该用户名关联的存储用户名/指纹对列表相对应。这种操作挫败了黑客,因为即使他们设法访问了列表,他们也无法推导出用户的密码,因为实际上不可能从指纹转到密码。他们也无法生成另一个具有相同指纹的密码来愚弄服务器,因为实际上不可能创建冲突。
尽管如此,没有一种方法是万无一失的,主要网站频繁遭到黑客攻击的报告就突显了这一点。例如,2016 年,雅虎!有 10 亿个帐户的数据被盗!
为了增加安全性,有时会使用一种称为加盐的方法来进一步阻止黑客利用被盗的用户名/指纹对列表。加盐是在每个密码中添加唯一的随机字符字符串。它确保即使两个用户使用相同的密码,存储的指纹也会不同。服务器上的列表将包含每个用户的三个组成部分:用户名、在密码中添加盐后派生的指纹以及盐本身。当服务器检查用户输入的密码时,它会添加盐,计算指纹,并将结果与其数据库进行比较。
即使在用户密码较弱的情况下,此方法也大大增加了黑客的工作难度。在不加盐的情况下,黑客可以计算字典中的所有指纹,并查看被盗数据中的指纹;可以识别黑客字典中的所有密码。通过加盐,对于使用的每种盐,黑客都必须计算黑客字典中所有密码的加盐指纹。对于一组 1,000 个用户,这将使使用黑客字典所需的计算量增加 1,000 倍。
适者生存
毋庸置疑,黑客有自己的反击方式。但他们面临着一个困境:他们最简单的选择要么需要大量的计算能力,要么需要大量的内存。通常这两种选择都不可行。但是,有一种称为彩虹表方法的折衷方法(请参阅“彩虹表帮助黑客”)。
在互联网、超级计算机和计算机网络的时代,密码设置和破解的科学不断发展——保护密码的人和决心窃取和可能滥用密码的人之间的无情斗争也在不断发展。
彩虹表帮助黑客
假设您是一名黑客,希望利用您已获得的数据。这些数据由用户名/指纹对组成,并且您知道哈希函数(请参阅“哈希黑客”)。密码包含在 12 个小写字母字符串的可能性空间中,这对应于 56 位信息和 2612 (9.54 x 1016) 个可能的密码。
至少有两种强大的方法可供您选择
方法 1。您滚动浏览整个密码空间。您计算每个密码的指纹 h(P),检查它是否出现在被盗数据中。您不需要大量内存,因为之前的结果会在每次新尝试时被删除,尽管您当然必须跟踪已测试的可能性。
以这种方式滚动浏览所有可能的密码需要很长时间。如果您的计算机每秒运行十亿次测试,您将需要 2612/(109 x 3,600 x 24) 天(1,104 天),或大约三年才能完成此任务。这个壮举并非不可能;如果您碰巧拥有一个由 1,000 台机器组成的计算机网络,一天就足够了。但是,每次您希望测试其他数据时(例如,如果您获得一组新的用户名/指纹对),重复此类计算是不可行的。(因为您没有保存计算结果,所以您将需要额外的 1,104 天来处理新信息。)
方法 2。您对自己说,“我将计算所有可能的密码的指纹,这将需要时间,并且我将把生成的指纹存储在一个大表中。然后,我只需在表中找到一个密码指纹即可识别被盗数据中的相应密码。”
您将需要 (9.54 x 1016) x (12 + 32) 字节的内存,因为该任务需要 12 字节用于密码,如果指纹包含 256 位(假设 SHA256 函数),则需要 32 字节用于指纹。那是 4.2 x 1018 字节,或 420 万个容量为 1TB 的硬盘驱动器。
此内存需求太大。方法 2 与方法 1 一样不可行。方法 1 需要太多的计算,而方法 2 需要太多的内存。这两种情况都很成问题:要么每个新密码都需要很长时间才能计算出来,要么预先计算所有可能性并存储所有结果的任务太大。
是否有某种折衷方案,既比方法 1 需要更少的计算能力,又比方法 2 需要更少的内存?确实有。1980 年,斯坦福大学的马丁·赫尔曼提出了一种方法,该方法在 2003 年由瑞士洛桑联邦理工学院的菲利普·厄克斯林改进,并在最近由法国雷恩国立应用科学学院 (INSA Rennes) 的吉尔达斯·阿沃因进一步改进。它需要比方法 1 更少的计算能力,以换取使用稍多的内存。
彩虹之美
以下是它的工作原理:首先,我们需要一个函数 R,将指纹 h(P) 转换为新密码 R(h(P))。例如,人们可以将指纹视为以二进制数字系统编写的数字,并将密码视为以 K 进制数字系统编写的数字,其中 K 是密码允许的符号数。然后,函数 R 将数据从二进制数字系统转换为 K 进制数字系统。对于每个指纹 h(P),它都会计算一个新的密码 R(h(P))。
现在,使用此函数 R, 我们可以预先计算称为彩虹表的数据表(之所以这样命名,可能是因为这些表以彩色方式描绘)。
为了在此表中生成数据点,我们从可能的密码 P0 开始,计算其指纹 h(P0),然后计算新的可能密码 R(h(P0)),即 P1。接下来,我们从 P1 继续此过程。除了 P0 之外不存储任何内容,我们计算序列 P1、P2、…直到指纹以 20 个零开头;该指纹被指定为 h(Pn)。这种指纹大约在 1,000,000 个指纹中出现一次,因为哈希函数的结果类似于均匀随机抽取的结果,而 220 大约等于 1,000,000。然后将包含以 20 个零开头的指纹的密码/指纹对 [P0, h(Pn)] 存储在表中。
计算了非常大量的此类对。每个密码/指纹对 [P0, h(Pn)] 代表密码序列 P0、P1、… Pn 及其指纹,但该表不存储那些中间计算。因此,该表列出了许多密码/指纹对,并代表了更多(中间值,例如可以从列出的对派生的 P1 和 P2)。但是,当然,可能存在差距:某些密码可能在所有计算链中都不存在。
对于几乎没有差距的良好数据库,存储计算对所需的内存比前面描述的方法 2 所需的内存小一百万倍。那不到四个 1TB 的硬盘驱动器。很简单。此外,正如将要看到的,使用该表从被盗指纹中派生密码是完全可行的。
让我们看看硬盘驱动器上存储的数据如何使您能够在几秒钟内确定给定空间中的密码。假设没有差距;表的预计算考虑了指定类型的所有密码——例如,从 26 个字母的字母表中提取的 12 个字符密码。
被盗数据集中的指纹 f0 可以通过以下方式用于揭示关联的密码。计算 h(R(f0)) 以得到新的指纹 f1,,然后计算 h(R(f1)) 以得到 f2,依此类推,直到您得到一个以 20 个零开头的指纹:fm。然后检查表以查看指纹 fm 与哪个原始密码 P0 关联。基于 P0,计算密码和指纹 h1、h2、…,直到您不可避免地生成原始指纹 f0,指定为 hk。您正在查找的密码是产生 hk 的密码——换句话说,是 R(hk – 1),即计算链中早一步的密码。
所需的计算时间是查找表中的 fm 所需的时间,加上从关联密码计算指纹序列(h1、h2、…、hk)所需的时间——这大约比计算表本身所需的时间短一百万倍。换句话说,所需的时间非常合理。
因此,通过进行(非常长的)预计算并仅存储部分结果,可以在合理的时间内检索具有已知指纹的任何密码。
以下序列表示从密码 (Mo, No, ..., Qo) 到指纹和其他密码的单独计算链,直到所需的指纹(以及因此在其之前的密码)弹出。 (长虚线表示可能与顶部两行相似的许多其他行。)
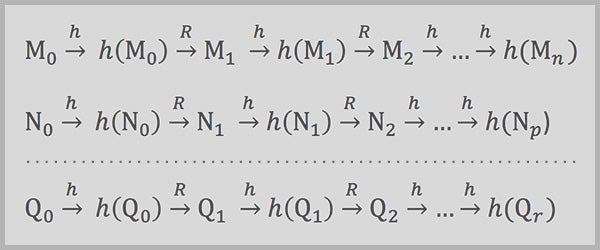
总而言之,通过知道每个计算链的开始和结束(预计算期间存储的唯一内容),黑客可以从指纹中检索任何密码。 在某种程度上简化的术语中,从被盗的指纹(称之为指纹 X)开始,黑客将重复应用 R 和 h 函数,计算一系列密码和指纹,直到达到前面有 20 个零的指纹。然后,黑客将在表中查找最终指纹(以下示例中的指纹 C)并识别其对应的密码(密码 C)。
示例表摘录密码 A—指纹 A
密码 B—指纹 B
密码 C—指纹 C
密码 D—指纹 D
接下来,黑客将再次应用 h 和 R 函数,从已识别的密码开始,继续操作,直到链中的一个生成的指纹与被盗的指纹匹配
示例计算密码 C → 指纹 1 → 密码 2-- → 指纹 2 → 密码 3…. → 密码 22-- →指纹 23 [与指纹 X 匹配!]
匹配项(指纹 23)将表明,从中派生指纹的前一个密码(密码 22)是链接到被盗指纹的密码。
必须进行许多计算才能建立彩虹表的首列和末列。通过仅存储这两列中的数据并通过重新计算链,黑客可以从其指纹中识别任何密码。

