猴子最终创作出莎士比亚作品的数学论证

在数学史上最离奇的研究实验之一中，英国普利茅斯大学的研究人员在附近的佩恩顿动物园给六只苏拉威西猕猴提供了一台键盘。从2002年5月1日到6月22日，这些动物通过敲击键盘来发泄情绪。它们输入的字母被传输到互联网上。科学家的目的是检验“无限猴子定理”：即猴子在键盘上随机打字，经过无限长的时间后，将产生所有可以想象的文本——包括莎士比亚全集。

但是——惊喜的是——这些灵长类动物的“诗歌”并没有达到目标。经过七个多星期，猕猴只产生了一份五页的文件，几乎完全由字母“S”组成。尽管如此，研究人员还是将结果作为一本书发表了。

为参与这项实验的六只猕猴 Elmo、Gum、Heather、Holly、Mistletoe 和 Rowan 辩护，它们没有无限的时间来完成这项工作。尽管如此，结果还是令人沮丧的。这些猴子能够创作出哈姆雷特或“苏格兰戏剧”似乎非常值得怀疑。

尽管这项研究绝没有驳斥无限猴子定理，但它表明，猴子不一定是按照该定理的创立者所假设的方式生成随机内容的理想候选者。无限猴子定理得名于数学家埃米尔·博雷尔，他在 1913 年用动物作为隐喻来说明他的概率论。然而，该定理背后的思想要古老得多。在古代，罗马哲学家和政治家马库斯·图留斯·西塞罗写道，有人可能“相信，如果将大量二十一个字母（由黄金或任何其他物质组成）扔在地上，它们会以清晰可辨的顺序排列，形成[史诗]《恩尼乌斯纪年》。[但是]我怀疑命运是否能从中创造出[甚至]一行诗。”

关于支持科学新闻报道

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道： 订阅。通过购买订阅，您正在帮助确保未来能够继续讲述关于发现和塑造我们当今世界的思想的具有影响力的故事。

正如佩恩顿动物园的猕猴所表明的那样，数学家们已经采取了创造性的步骤来探索这种可能性。今天的研究表明，西塞罗是错误的：诗歌可以从这种随机性练习中产生，前提是你能够等待很长时间。

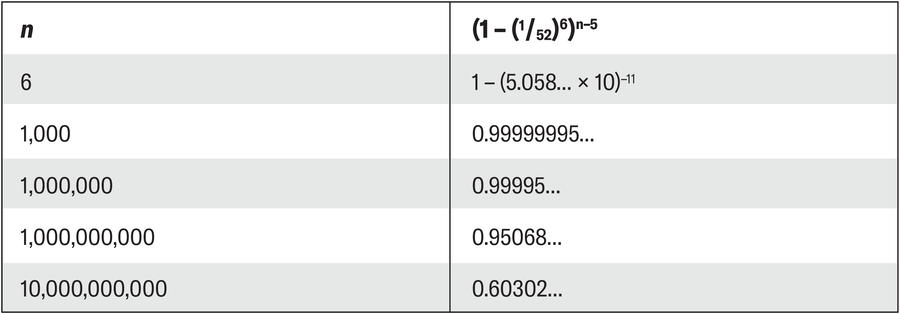
特定单词出现的概率

让我们用一个简单的例子来检验这个想法。当你随机按一系列字母键一定次数时，完全偶然地得到单词“banana”的可能性有多大？（在这种情况下，你不按任何数字或特殊字符。）如果你连续按六个键，每个键都是随机选择的，那么概率是 (¹⁄₅₂)⁶ = ¹⁄_19770609664，约为百分之一的五十亿分之一。换句话说，不打出 banana 的概率是 1 – (¹⁄₅₂)⁶，这几乎是 1。总的来说，如果你随机按六个键，那么得到单词 banana 的可能性非常小。但是，如果你按键的时间更长呢？

如果你随机按七个键的序列，则有两个连续的六个字母的段可以形成所需的单词。按八次键，则有三个六个字母的字符串，依此类推。如果你随机按键盘 n 次，则单词 banana 不会出现在字符串中任何位置的概率为 (1 – (¹⁄₅₂)⁶)^n–5。对于 n 值不断增加的情况，不出现 “banana” 的几率逐渐降低

因此，“banana” 出现的几率逐渐提高：如果你在键盘上随机按键 100 亿次，那么该单词出现在某处的概率突然约为 40%。n 值越大，找到单词 banana 的概率就越接近于 1。当然，这个结果也适用于其他字母序列、单词，甚至整个句子和书籍。因此，从数学的角度来看，西塞罗是错误的。

实践中的无限猴子定理

2024 年，巴西圣保罗大学的数据分析师 Ergon Cugler de Moraes Silva 想要 выяснить 平均需要多长时间才能偶然获得莎士比亚的作品。他没有使用猴子，而是编写了一个字符生成器程序。正如在一篇预印本论文中所描述的那样，他的技术旨在每秒快速生成数百个伪随机空格、标点符号和字母（包括大写和小写），直到出现《哈姆雷特》中的一句名言：“生存还是毁灭，这是一个问题”（包括空格）。

库格勒分几个步骤进行。首先，他研究了平均需要多长时间才能单独找到字母“T”。他重复了该过程 10 次，然后记录了生成所需输出所需的平均时间和字符数。然后，他重复此过程以确定随机生成 “To” 需要多长时间，然后再次对 “To” 后跟一个空格进行同样的操作，依此类推。

如下表所示，他的程序必须随机生成约 60 个字符才能产生 “T”，并且平均生成了 345,380,940 个字符才能产生 “To be”。这两个词也花费了他的程序大约 1,100 秒（略多于 18 分钟）。

此时，库格勒遇到了瓶颈。考虑到正确生成句子中的下一个字符所需的时间不断增加，他意识到这项任务可能需要他的程序不断地输出字符，直到人类灭绝（假设所涉及的计算机能够持续运行那么长时间）。因此，在第二步中，库格勒设计了一个程序，该程序使用先前确定的数据来推断生成整个句子所需的字符数和计算时间。

库格勒的计算表明，要让 “生存还是毁灭，这是一个问题” 出现，需要极大的耐心：大约需要生成 2.68 x 10⁶⁹ 个字符，这将花费大约 2.95 x 10⁶⁶ 秒，或 9.35 x 10⁵⁸ 年。

由于我们宇宙的年龄估计为 138 亿年，因此我们必须等待的时间几乎是宇宙大爆炸至今这段时间的 7 x 10⁴⁸ 倍。而这一切仅仅是为了偶然产生《哈姆雷特》中的一句话。在这方面，西塞罗是对的：在有限的时间内，偶然性不太可能产生一首诗，甚至任何其他文本的一行可读诗句。

本文最初发表于Spektrum der Wissenschaft，经许可转载。