即使数学令人费解,它也是美丽的。摄影师杰西卡·温妮在 2018 年开始拍摄世界各地数学家的黑板时,就着手捕捉这种魅力。“我一直对进入我知识领域之外的世界感兴趣,”温妮说。在不理解黑板上的数学代表什么的情况下,她能够在纯粹的审美层面上欣赏它。“这与我观看抽象画时的感觉相似。但它增加了更多的趣味,因为在表面之下有伟大的意义和伟大的深度,他们正试图揭示普遍真理。”
当温妮与两位在她科德角避暑别墅附近度假的数学家成为朋友时,她第一次被数学世界所吸引。当她了解他们的研究时,她发现数学过程和艺术过程之间有许多相似之处。“我真的很惊讶地看到他们如何工作以及他们所做的事情是多么有创意,”她说。
随着温妮开始前往不同的大学会见更多的数学家,她发现他们的黑板风格是多么多样化。“有些非常干净整洁,并且经过非常仔细的考虑,”她回忆道。“而有些则只是这种爆发和混乱。黑板几乎感觉像是人物的肖像,并且取决于数学家的个性。”
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的有影响力的故事的未来。
许多照片将收录在《不要擦除:数学家和他们的黑板》一书中,该书将于 6 月由普林斯顿大学出版社出版。温妮打算继续这个项目,尤其因为她的旅行因疫情而中断。她原计划参观剑桥大学的数学系,直到她得知他们的黑板都已被白板和数字板取代。“我非常喜欢在黑板上工作的模拟性质,”她说。“我注意到很多地方都在摆脱他们的黑板,我感到有记录这一点的紧迫性。”

致谢:杰西卡·温妮
混合高斯分布
物理测量(例如从人群中随机选择的女性的身高)通常会产生一种称为高斯分布的分布,其图看起来像一座圆润的山峰。机器学习算法通常会获得异构数据(例如,随机女性和男性的身高),一项具有挑战性的任务是将测量结果分解为两个或多个组成部分。麻省理工学院的安库尔·莫伊特拉和他的同事们发现了一种分离曲线的方法,该方法仅需要混合物的头六个“矩”——特殊特征。“我在黑板上画的是我们论文中的关键证明,”莫伊特拉说。“事实证明,这等同于能够取两个不同的混合物,将它们相减,并表明结果函数最多穿过零轴六次。”
致谢:杰西卡·温妮
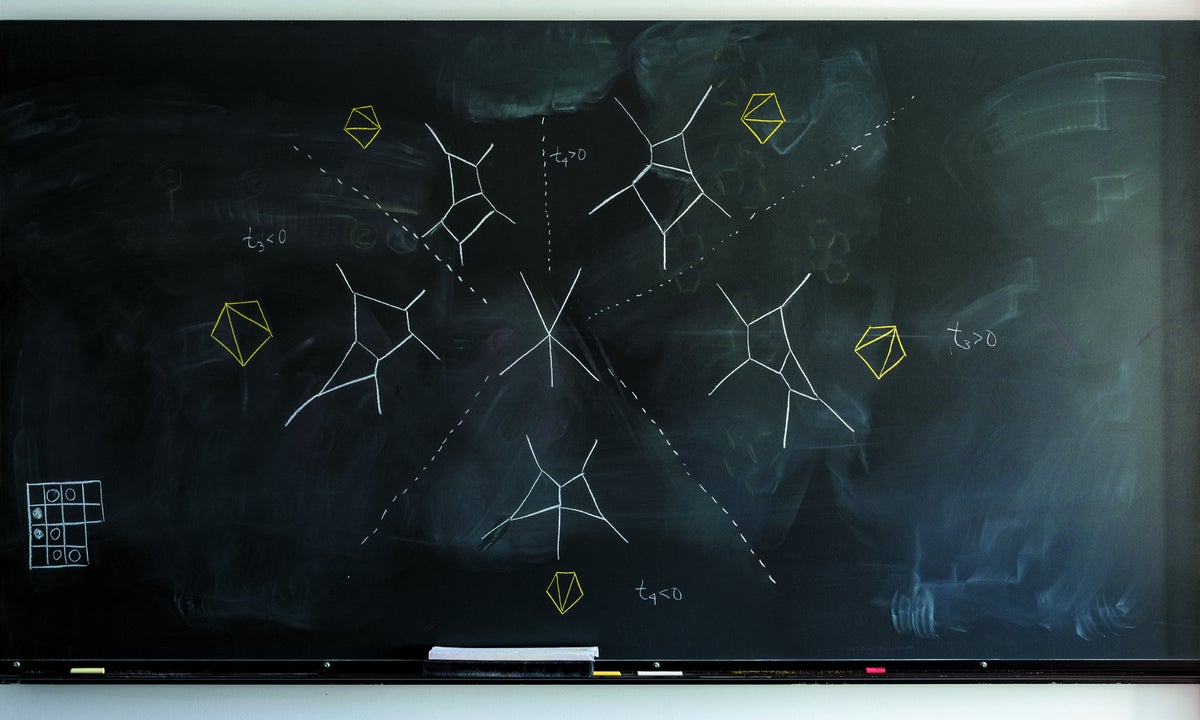
分支波
类似火柴人的图表代表了波演化的快照。白色线条编码了特定时刻浅水波配置的波峰位置。“这些波具有有趣的相互作用,”哈佛大学数学家劳伦·K·威廉姆斯解释说。“例如,两个波可以相遇并形成一个波出来,如果让时间变化,就会看到不同的波相互作用模式。” 威廉姆斯和她的合作者俄亥俄州立大学的 Yuji Kodama 使用这些图表来研究所谓的 Kadomtsev-Petviashvili (KP) 方程的解,该方程描述了波的行为。他们发现,由某一类解产生的波模式可以通过多边形的三角剖分(黄色)进行分类。“如果稍微改变解的参数,这些波模式可能会退化并形成,例如,中心显示的白色‘海星’图案,”她说。左下方是 Kodama 和 Williams 称之为“围棋图”的东西,以棋盘游戏围棋命名,他们用它来研究 KP 方程的某些解。

致谢:杰西卡·温妮
外出散步
每条彩色线都显示了行人在这个“顶点模型”中穿过正方形网格的路径。行人的路径不能重叠,因此每当两个人相遇时,他们都必须决定每个人将走向哪个方向。该决定可能存在偏差——例如,与颜色较暖的步行者相比,颜色较冷的步行者可能更倾向于向东而不是向北走。“尽管它的描述很简单,但它的大规模行为是复杂的,并且与许多数学和物理现象密切相关,”麻省理工学院的数学家阿列克谢·博罗丁说。顶点模型可以扩展到包括更多的步行者和更多的颜色。“欺骗性的简单性、隐藏的深度以及数学在分析中的有效性使这个系统对我很有吸引力。” 博罗丁还喜欢“美学因素”,他补充道。
致谢:杰西卡·温妮
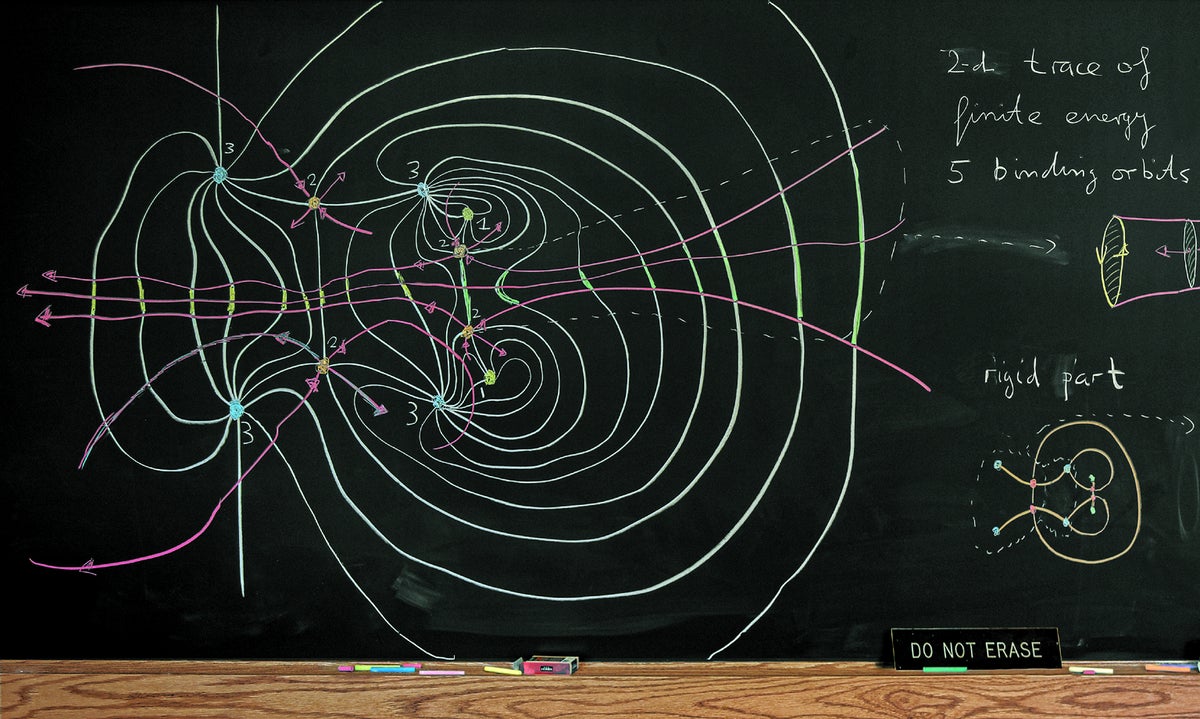
有组织的混乱
事实证明,混乱中可能存在秩序。在 1999 年至 2003 年间,新泽西州普林斯顿高级研究所的赫尔穆特·霍费尔和他的同事们开发了一个研究这种秩序的领域,称为辛动力学。霍费尔的黑板描绘了“有限能量叶理”(白色线条)——用于表征动力学系统(例如在地球和月球之间移动的卫星)中混乱的工具。这个复杂的表面系统与卫星的位置和动量随其与两个行星体的引力相互作用而演变有关。霍费尔希望“这种对混乱的更好理解最终将应用于航天任务的设计”。例如,早期的努力利用了关于混乱的见解来节省太空探索期间的燃料,但代价是增加了旅行时间。霍费尔认为,这项新工作可以进一步提高燃油效率,而不会延长任务的持续时间。
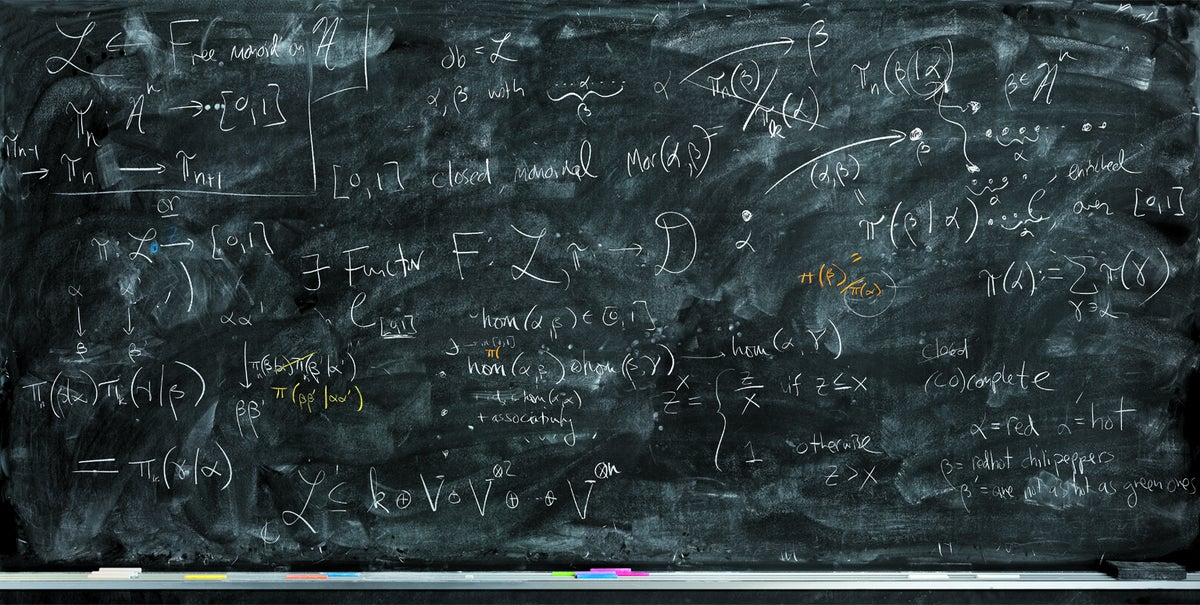
致谢:杰西卡·温妮
匹配形状
根据拓扑学的数学领域,咖啡杯和甜甜圈是著名的“相同”形状,拓扑学根据表面包含的孔洞数量对其进行分类。因为咖啡杯和糕点都只有一个孔,并且可以弯曲和拉伸成相同的形状而无需进行任何切割或穿孔,所以它们在拓扑上是相同的。同样,标记为“2”的两个表面以及标记为“6”的表面在根本上是相同的。“它们非常有趣,”新泽西学院的数学家南希·欣斯顿说,她在微分几何学中研究此类形状上的路径。
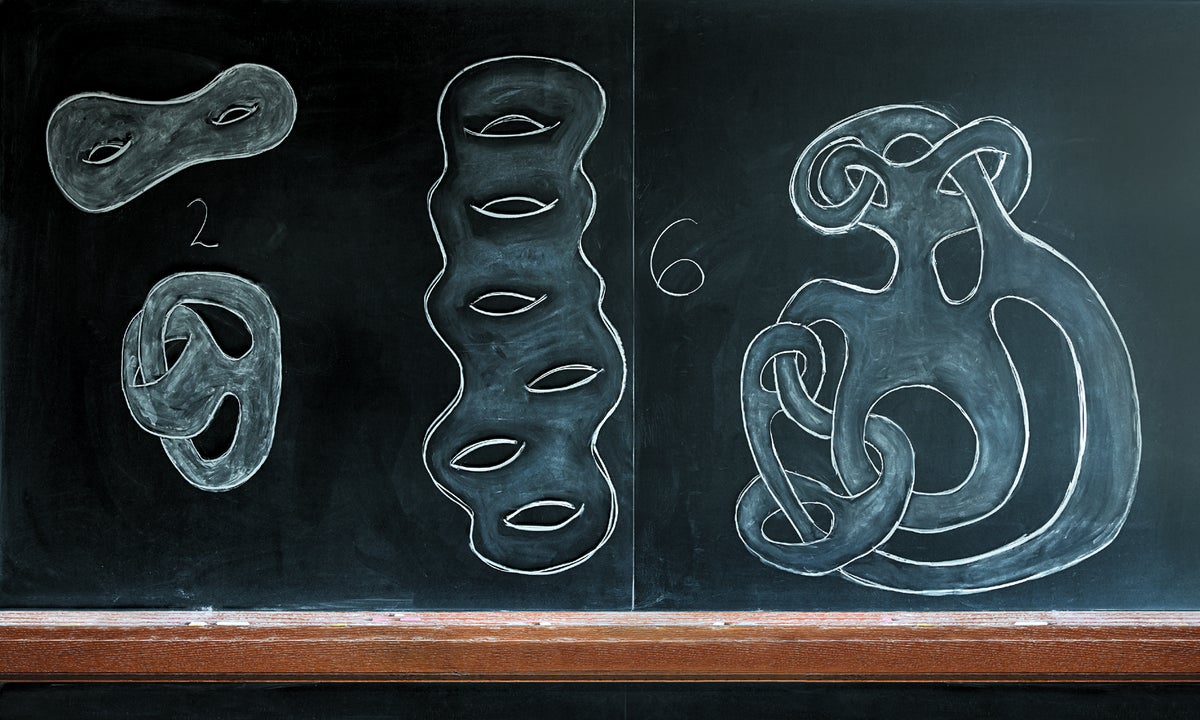
致谢:杰西卡·温妮
合作
黑板通常是数学合作的最佳工具——视觉和触觉场所,可以融合两个人的想法和直觉。皇后学院的数学家约翰·特里拉和 X,月球工厂的 Tai-Danae Bradley 试图理解自然语言中隐藏的数学结构。“那是我们第一次谈到以特定方式形式化这种结构,”特里拉说。“我和泰伊在黑板上一起工作,它显示了我们两个人的写作。例如,大的‘存在[用 表示]函子 F’是我的;下面的‘hom(alpha, beta) in [0,1]’是泰伊的。” 这项研究是特里拉寻找“幕后工作以了解正在发生的事情”的总体探索的一部分,他说。“在抽象层面上升一级来解释某些事情有点像特意爬山环顾四周——在研究中很有用,因为它可以显示在未知领域的前进方向。”

致谢:杰西卡·温妮
解码拓扑学
特里拉和布拉德利还与数学家和数据科学家泰勒·布赖森合作编写了教科书《拓扑学:分类方法》。他们讨论了如何最好地呈现材料,他们的黑板代表了他们旨在传达的一些内容。“上面的内容不是研究——它都是典型的博士生在拓扑学课上会学习的标准数学,”特里拉说。
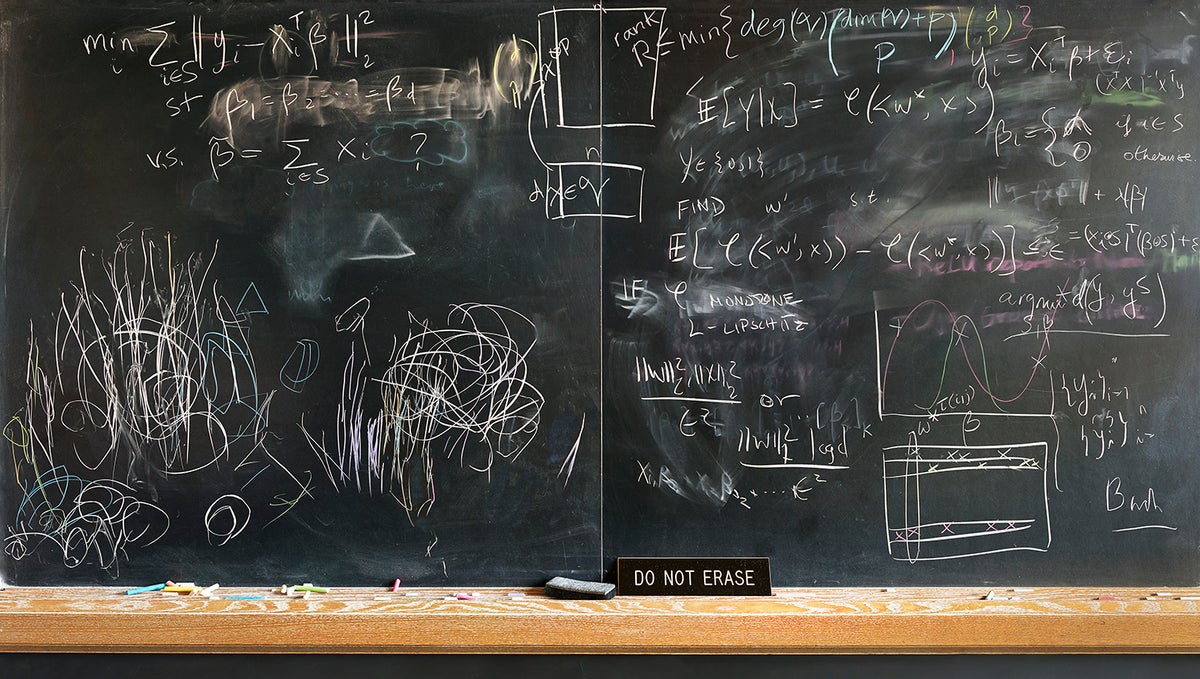
致谢:杰西卡·温妮
进行中
密歇根大学电气工程师和计算机科学家劳拉·巴尔扎诺研究机器学习和信号处理的数学模型。“在特别的一天,我和两位学生和一位同事分享了关于几个不同问题的想法,”她回忆道。“事实上,现在黑板左上角的部分对我来说几乎没有意义。黑板右下角的部分是我一年后仍在研究的东西,几乎没有任何进展。右侧黑板的其余大部分内容现在已经发表了!” 对于外行人来说,左下角最后一部分可能与其余部分一样难以理解,但巴尔扎诺说,那部分是她当时 2.5 岁的女儿画的。“粉笔是让她保持专注的好方法——至少 15 分钟。”

致谢:杰西卡·温妮
无限度映射
从一个函数开始,或 f, 用复数定义,或 z。当一个数是复数时,这意味着它包含一个虚部——即 -1 的平方根。然后迭代函数的连续版本 z 以创建函数的轨道。接下来取接近 z 的点并查看它们的轨道。此过程描述了该函数的动力系统。纽约市立大学研究生中心的数学名誉教授琳达·基恩对无限度函数的动力系统感兴趣。“我对无限度映射很感兴趣,”基恩说。“这些图片旨在帮助理解当您更改无限度的 f 时会发生什么。”

