数学家们今年非常忙碌:他们发现了迄今为止最大的素数,一个新的圆周率公式,约翰·塞巴斯蒂安·巴赫音乐中的神秘模式,甚至一种全新的新型形状。其中一些发现是实用的——例如,新发现的形状出现在自然界中,并已被用于创意建筑设计。另一些,例如 4100 万位数的素数,用处不大——但都令人着迷。以下是我们今年撰写的一些最令人兴奋的数学发现。
新形状问世
一位数学家想知道,一个形状最少需要有多少个角才能仍然能够无缝隙地完全覆盖一个表面。这个难题促使他和他的同事们发现了以前从未在数学上描述过的形状,称为软细胞。虽然软细胞对数学家来说是新的,但事实证明,软细胞存在于鹦鹉螺壳、红细胞和自然界的其他元素中。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将有助于确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
超长素数
素数——只能被 1 和自身整除的数字——长期以来一直让数学家着迷。今年,一位研究人员发现了已知的最大素数,它拥有惊人的 41,024,320 位数字。自上次发现新的素数以来已经过去了六年,而且搜索变得越来越困难,因为素数随着它们的增长而彼此之间分布得更远。
圆周率新公式
圆周率 (π) 的概念,即圆的周长与其直径的比率,自古代巴比伦以来,4000 年来一直广为人知。但是,计算这个无理数的精确位数一直是一个挑战。最近,物理学家使用弦理论提出了一种全新的计算圆周率的方法。
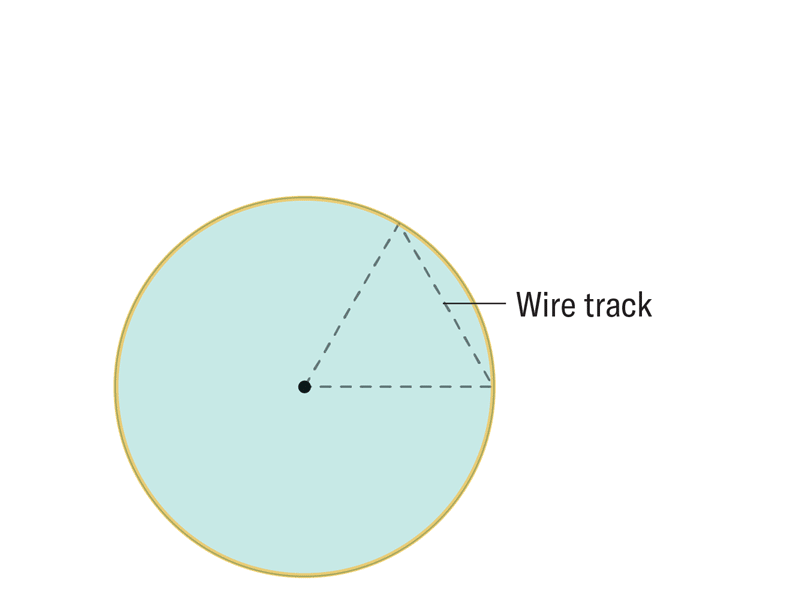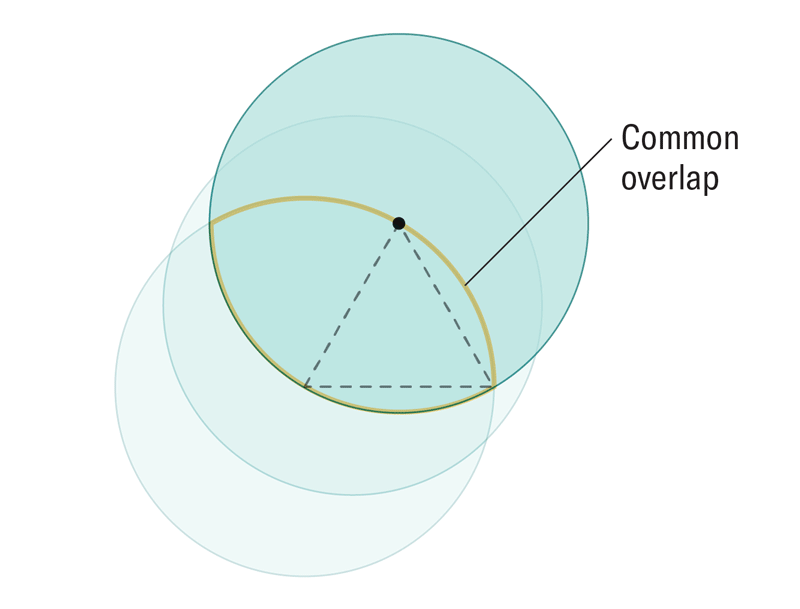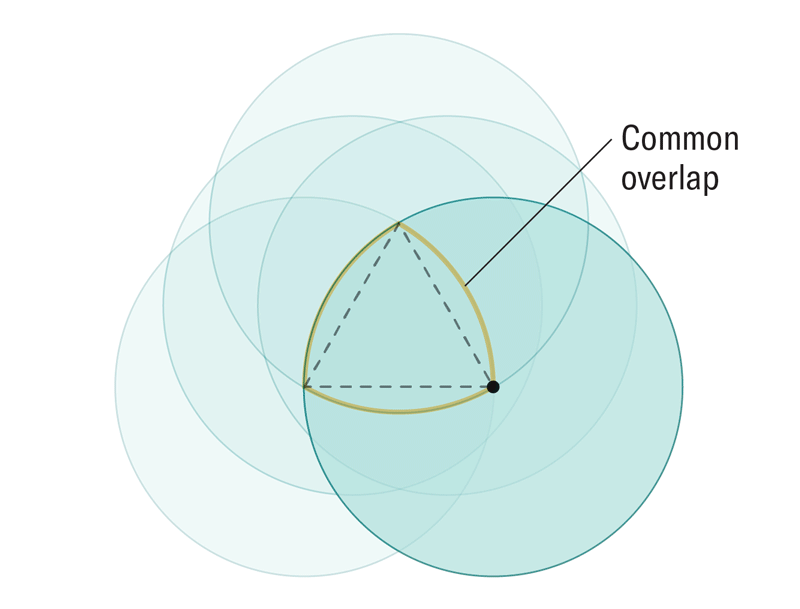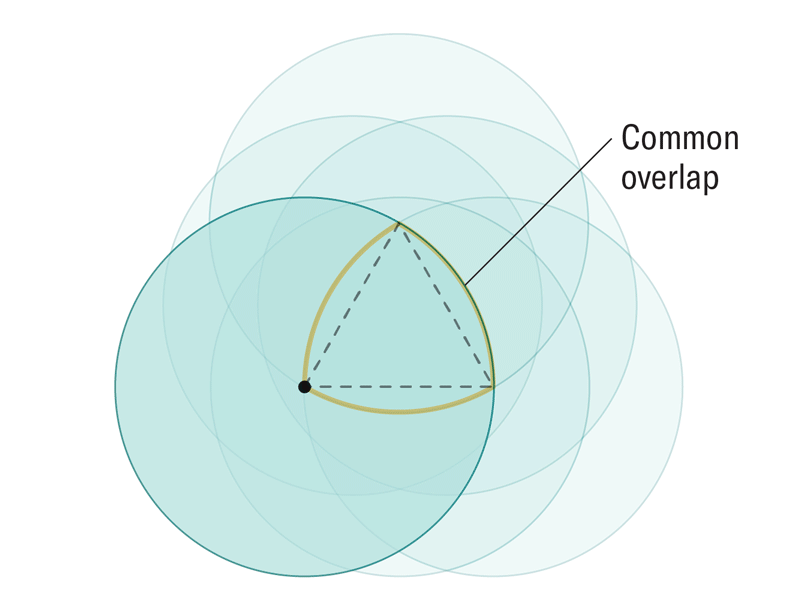
阿曼达·蒙塔内斯
多维度轮子
40 年来,数学家们一直在思考一个问题:我们如何在任何维度中找到具有最小体积的等宽形状?研究人员最近设想了一种新型的多维轮子来回答这个问题。这种新型轮子可以在任何维度上构建,其尺寸仅为传统滚动形状(如圆形或球体)的一小部分。
计算不可计算之物
这项突破与数学中的一个基本真理有关:并非所有事物都可以计算,无论人们多么努力(或海狸多么忙碌)。一种特殊的不可计算表达式称为忙碌海狸函数。它的值,称为 BB(n),对于所有数量的 n 永远不会被知道,但一个名为“忙碌海狸挑战”的国际合作项目最近成功确定了该函数的第五个值——这让认为这不可能的数学家们感到惊讶。

巴赫的键盘乐器前奏曲乐谱。
PFMphotostock/Getty Images
J. S. 巴赫的隐藏信息
科学家们将巴洛克作曲家约翰·塞巴斯蒂安·巴赫创作的乐谱转化为数学网络,并分析了他的不同风格的变化。他们使用信息论来查找他音乐中的模式,这些模式有助于解释巴赫如何通过他的作品传达信息——包括音乐、数学和情感信息。
缺失的瓷砖
数学家们长期以来一直想知道,是否有一种单一的形状可以铺满一个表面——也就是说,完全覆盖一个平面——而不产生重复的图案。许多人怀疑是否存在这样一种形状,即所谓的爱因斯坦瓷砖,但研究人员最终发现了一种。虽然这种瓷砖是在 2023 年宣布的,但参与其中的一位数学家今年向我们讲述了幕后故事。
