在20世纪70年代早期,数学家唐纳德·克努特与他的妻子在挪威度过了一个学术休假。这段时间本应是用来放松的。然而,一天晚上,他惊醒了他的伴侣,情绪激动。他迫切需要写一本书。他向他的配偶保证,别担心,只需要一周时间。为了专心写作,他在奥斯陆为自己预订了一间酒店房间。
在那里,他起草了后来成为超现实数:两位前学生如何转向纯粹数学并找到完全的幸福的书。尽管克努特并没有发明超现实数的概念,但他却是第一个发表关于该主题的详细著作并创造了这个术语的人。时至今日,他的书仍被认为是该主题的标准著作。
然而,这部著作绝非普通的非小说类作品。它由两个虚构人物爱丽丝和比尔之间的对话组成。书中还介绍了超现实数的真正发明者,已故的数学家约翰·霍顿·康威,他于2020年去世。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于发现和塑造我们当今世界的想法的具有影响力的故事。
“起初,一切皆为空虚,J.H.W.H. 康威开始创造数字,”克努特写道。克努特在康威的名字中添加了额外的首字母,以暗示四字神名(希伯来语中上帝的四字名字,音译为 YHWH 或耶和华),他在 Numberphile 的 YouTube 视频中解释道。
这绝非唯一的圣经典故;甚至克努特撰写这本书的背景故事也呼应了宗教创世故事。他只用了一周的时间就把整本书写成了文字,正如他向妻子承诺的那样。“在第六天我完成了它。在第七天我休息了,”克努特告诉 Numberphile。
超现实数是通过在两个给定的现有数字之间添加值来创建的。例如,如果您查看 0 和 1,则 1/2 在中间,1/4 在 0 和 1/2 之间,依此类推。这种方法使得越来越精确地解析数轴成为可能。
这个想法乍听起来并不引人注目,但是,与简单地提供分母越来越大的分数不同,在某个时刻,一切都会爆炸,突然之间,出现了甚至不包含在实数中的值。
两个公理产生一个不可思议的数字宇宙
康威建立了两个基本规则,从中产生了不可估量的数字领域。每个数字 x 由两个集合 ML 和 MR 定义,它们包含先前创建的数字:x = {ML : MR}。
ML 是左手集,MR 是右手集。第一个规则是左手集的元素始终小于右手集的元素。
第二个规则规定,0 是由两个空集界定的数字。这两个规则为数学的一个极其多样化的分支奠定了基础!

超现实数 x 来自于位于两组数字 ML 和 MR 之间的值。 来源:Manon Bischoff/Spektrum der Wissenschaft,由 Amanda Montañez 重新设计
在这些基础之上,克努特的超现实数创世故事发生在几天之内。在第零天,根据第二条规则,0 从无到有地被创造出来,他将其表示为 0 = { : }。
在第一天,又创建了两个数字:1 = {0: } 和 –1 = { :0}。这两个数字之所以出现,是因为它们是数轴上第二大和第二小的整数(分别是)。
超现实创造的第二天变得更加有趣。现在你可以第一次使用不同的数字了。例如,{0:1} 表示介于 0 和 1 之间的数字,即 1/2。你也可以创建 {1: } = 2, {–1:0} = –1/2 和 { :–1} = –2。
以这种方式继续下去,在第三天,你将得到 1/4、3/4、3 等等。
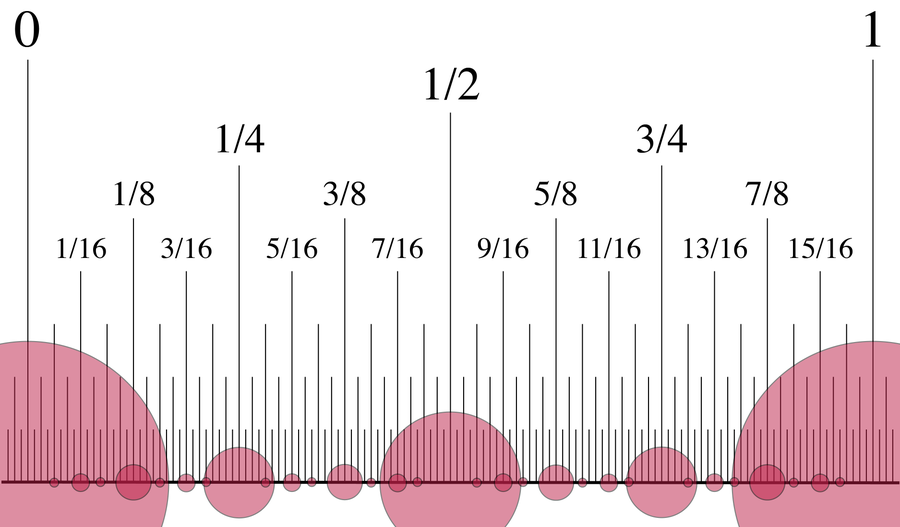
分母为 2 的倍数的分数在超现实数的创建中逐渐出现。 来源:David Eppstein/Wikimedia Commons(CC0 1.0)
如果你坚持下去,到第 n 天,你将拥有从 –n 到 n 的所有整数,以及分母为 2, 22, 24, 28,... 到 2n 的所有分数。这种分母是 2 的倍数的分数称为二进有理数。这使得超现实数看起来相当枯燥:它们仅由整数和二进有理数组成。没有 π (π) 或根号二 (√2) 等值的踪迹——甚至连像 1/3 这样微不足道的数字也没有。
所有实数的黎明
超现实数真正令人兴奋的特性在你到达 ω 天时就会展开。ω 这个符号对应于可数无穷大。在这一天,所有以前不存在的实数,即所有无理数值和所有非二进有理分数,都会一下子被创造出来。
例如,√2 来自以下表示:√2 = {1 5/411/8 ... : ... 23/163/2}。其他无理数值(如 π)也以这种方式获得;该数字由两个二进有理数序列包围。
实际上,该过程类似于已建立的戴德金分割方法,该方法用于从有理数构造实数。在该方法中,形成两组有理数,其中一组包含小于另一组的数字(就像康威的第一条规则一样)。然后,这两组之间的“交集”定义了一个实数。
但在康威的奇特构造中,ω 天诞生了新的数字。突然之间,无限值也出现了——即数字 ω。为此,你必须将所有自然数插入左手集,并将右手集留空:ω = {1 2 3 ... : }。这对应于大于所有自然数的数字。
还有更不寻常的东西。如果你在左手集中输入 0,并在右手集中输入所有二进有理分数,你将得到一个无穷小数 ε = {0 : ...1/81/41/2 1}。这个 epsilon 代表无穷大的倒数:ε 非常小,以至于没有实数可以表示它。事实上,ε 对应于 ω 的倒数:ε = 1/ω。无穷小数 ε 不仅在 ω 天单独出现,而且还与所有整数和二进有理数组合出现: 1/2 + ε = {1/2 : ... 1/81/41/2 1}。
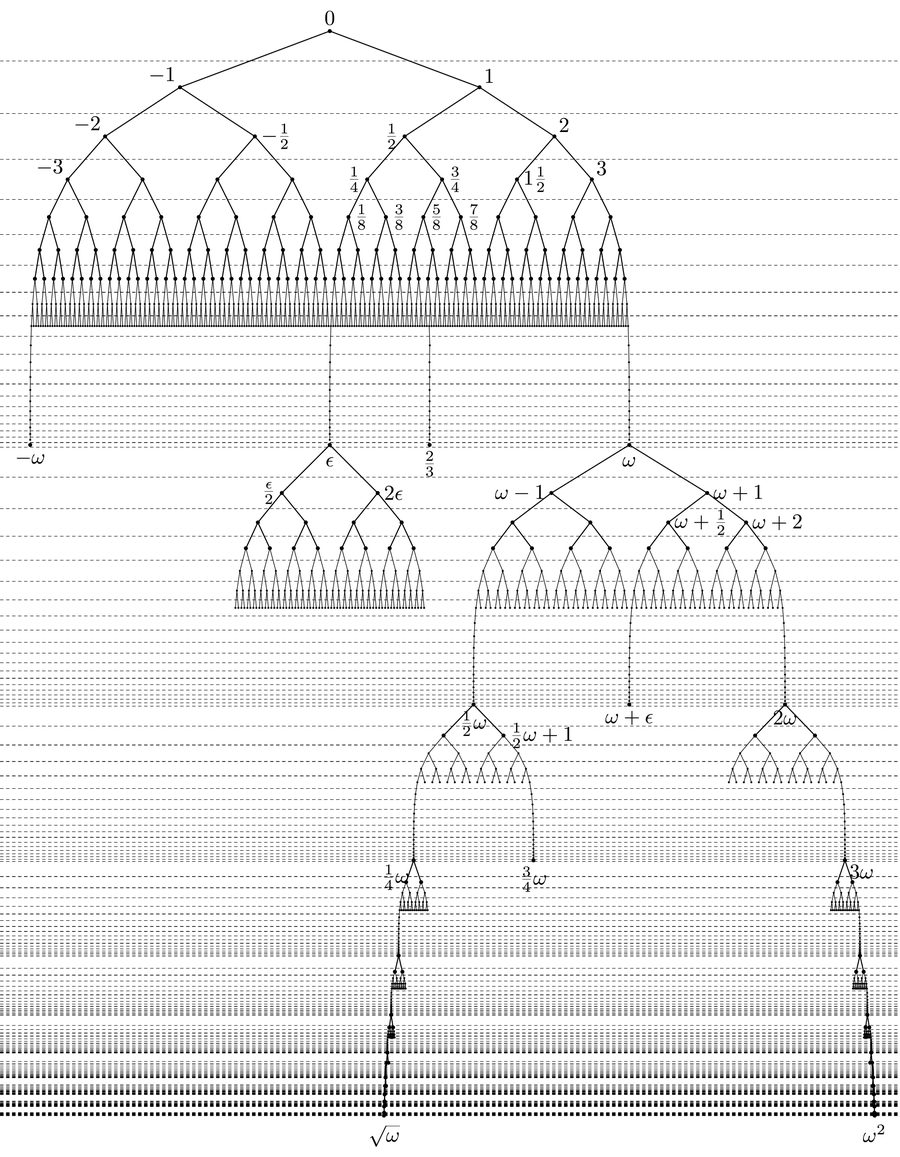
经过无限多天后,从分数到无理数,再到无穷大和无穷小,各种各样的数字都被创造出来了。 来源:Lukáš Lánský/Wikimedia Commons(CC BY-SA 3.0)
在 ω + 1 天,出现了更多的超现实数,例如数字 ω + 1 和 ω – 1,两个新的无穷大。此外,任何实数现在都可以与 ε 组合,例如:π + ε = {π : ...1/81/41/2 1}。此外,还创建了数字 ε/2,这是一个比无穷小数小一半的值。
数量的概念崩溃了
在随后的每一天,都会出现新的超现实数:新的无穷大和无穷小,以及出现在所有先前生成的数字之间的新值。数字的多样性一点一点地继续增长。事实上,创造了如此多的对象,以至于超现实数不再能被定义为一个集合。相反,它们形成一个“类”。因此,它们远远超过所有其他类型的数字:自然数、有理数和实数。
为了理解这一点,回想一下超现实数的定义,即两个集合 ML 和 MR,其中 ML始终是较小的那个。假设所有超现实数的总体是一个集合 S。那么你可以将一个新数字 x 定义为 x = {S : }。这将使 x 成为一个超过 S 所有值的数字——所以你将定义一个不包含在 S 中的超现实数。
这是一个矛盾,因为根据定义,S 包含所有超现实数。为了避免这种悖论(如果你想确定所有无穷大的数量,也会出现这种悖论),数学家们引入了类的概念。因为 S 是一个类,所以它不能用于构造超现实数。
超现实数还隐藏着更多的惊喜。尽管超现实数的数量明显多于实数,但它们并没有形成连续统。由超现实数组成的数轴充满了漏洞——不像实数轴那样没有间隙。这些空间的原因是,总是有更小的无穷小量挤在先前生成的超现实数之间。
例如,开集 [0,1) 包括所有小于 1 的值。因此,数字 1 是一个“上限”。然而,超现实数缺少这样的概念。那是因为你可以在集合 [0,1) 和 1 之间找到一个超现实数,例如 1 – ε。这个数字既不属于 [0,1) 也不属于 1。

与实数轴不同,超现实数轴包含较小的无穷小量可以容纳的间隙。 来源:Manon Bischoff/Spektrum der Wissenschaft,由 Amanda Montañez 重新设计
这一观察具有深远的意义。这意味着诸如 1/n 之类的数字序列,如果 n 趋于无穷大,则不具有极限值 0。相反,该序列不会收敛。它将永远持续运行,同时它将取越来越小的值 ε, ε/2, ..., ε/100, 等等。在超现实数的宇宙中,0.9999... 永远不可能等于 1——不像实数那样。
由于缺少这样的极限,我们在学校以导数和积分形式学习的常用分析形式也崩溃了。所有基本概念都基于极限值形成和连续数空间。然而,专家们已经成功地开发出所谓的“非标准分析”,它可以与超现实数一起使用。
即使这一切看起来非常抽象和陌生,克努特也确信,超现实数与其他任何数字一样,都适合描述我们的世界。如果“一百年来每个人都在学校里学到这个,[他们就会]认为这就是数字的样子,”他告诉 Numberphile。“我们没有理由认为宇宙会遵守实数的定律。”事实上,物理学家已经尝试将超现实数纳入他们的理论。然而,所涉及的工作通常非常繁重,到目前为止,收益甚微。
在数学中,超现实数形成了一个有趣的结构:一个庞大的数字系统,可用于描述无穷大和无穷小。康威实际上是在研究围棋的策略时提出了这种惊人的构造。超现实数已在博弈论中证明了自身的价值,但仅限于其有限的变体,即整数和二进有理数的并集。正如康威在2016 年的一次讲座中所反思的那样,他以这种方式揭示了以前未知的超现实数宇宙的无限广阔是他“数学生活中最大的惊喜。”
本文最初发表于Spektrum der Wissenschaft,并经许可转载。
