普遍“常数”的漂移可能揭示空间的隐藏维度

有些事物永恒不变。物理学家称之为自然常数。例如光速c，牛顿引力常数G，以及电子质量m_e等量，被认为在宇宙的所有地点和时间都是相同的。它们构成了物理学理论建立的支架，并定义了我们宇宙的结构。物理学的进步是通过对它们的值进行越来越精确的测量来实现的。

然而，令人惊讶的是，没有人成功地预测或解释过任何常数。物理学家不知道为什么常数会取它们所取的特殊数值（给定单位的选择）。在国际单位制中，c 是 299,792,458；G 是 6.673 × 10⁻¹¹；m_e 是 9.10938188 × 10⁻³¹——这些数字没有明显的规律。贯穿这些数值的唯一线索是，如果其中许多数值哪怕稍微不同，像生物这样的复杂原子结构就不可能存在。解释常数的愿望一直是推动发展对自然界的完整统一描述，或“万物理论”的动力之一。物理学家一直希望，这样一种理论将表明，每个自然常数都只能有一个逻辑上可能的值。它将揭示自然界看似任意性背后的潜在秩序。

然而，近年来，常数的地位变得更加模糊，而不是更清晰。研究人员发现，万物理论的最佳候选者，即弦理论的一种变体，称为M理论，只有在宇宙具有超过四个时空维度（多达七个维度）的情况下才是自洽的。一个隐含的意义是，我们观察到的常数可能实际上不是真正基本的常数。那些常数存在于完整的高维空间中，而我们只看到它们的三维“阴影”。

支持科学新闻报道

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅，您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。

与此同时，物理学家也开始意识到，许多常数值可能是纯粹偶然的结果，是在宇宙早期历史中的随机事件和基本粒子过程中获得的。事实上，弦理论允许存在大量的——10⁵⁰⁰——可能的“世界”，它们具有不同的自洽定律和常数集。到目前为止，研究人员还不知道为什么选择了我们的组合。继续研究可能会将逻辑上可能的世界的数量减少到一个，但我们必须对令人不安的可能性保持开放态度，即我们已知的宇宙只是众多宇宙之一——多重宇宙的一部分——并且多重宇宙的不同部分展示了该理论的不同解，我们观察到的自然定律仅仅是许多地方法规系统中的一个版本。

那么，对于我们的许多数值常数，除了它们构成了一种罕见的组合，允许意识进化之外，就不可能有进一步的解释了。我们可观测的宇宙可能是被无限的无生命空间包围的众多孤立绿洲之一——一个超现实的地方，在那里，不同的自然力占据主导地位，而像电子这样的粒子或像碳原子和DNA分子这样的结构可能是不可能存在的。如果你试图冒险进入那个外部世界，你将不复存在。

因此，弦理论用右手给予，却用左手拿走。它部分是为了解释物理常数看似任意的值而设计的，该理论的基本方程几乎不包含任意参数。然而，到目前为止，弦理论没有对观测到的常数值给出解释。

您可以信任的尺子

事实上，“常数”这个词可能用词不当。我们的常数可能会随时间和空间而变化。如果额外的空间维度的大小发生变化，我们三维世界中的“常数”也会随之变化。如果我们向太空深处足够远的地方观察，我们可能会开始看到“常数”已稳定为不同值的区域。自 20 世纪 30 年代以来，研究人员一直在推测常数可能不是恒定的。弦理论为这一想法提供了理论上的合理性，并使观察者寻找偏离常数的偏差变得更加重要。

此类实验具有挑战性。第一个问题是实验室设备本身可能对常数的变化敏感。所有原子的大小都可能在增加，但是如果您用来测量它们的尺子也在变长，您将永远无法分辨出来。实验者通常假设他们的参考标准——尺子、质量、时钟——是固定的，但在测试常数时他们不能这样做。他们必须关注没有单位的常数——它们是纯数字——因此它们的值与单位制无关。一个例子是两个质量的比率，例如质子质量与电子质量之比。

一个特别令人感兴趣的比率结合了光速c，单个电子的电荷e，普朗克常数h，以及所谓的真空介电常数ε₀。这个著名的量，精细结构常数 α (α) = e²/2ε₀hc，最早由阿诺德·索末菲于 1916 年引入，他是将量子力学理论应用于电磁学的先驱。它量化了涉及真空中带电粒子的电磁 (e) 相互作用的相对论 (c) 和量子 (h) 特性 (ε₀)。经测量，α 等于 1/137.03599976，或大约 1/137，这赋予了数字 137 在物理学家中传奇般的地位（它通常打开他们公文包上的密码锁）。

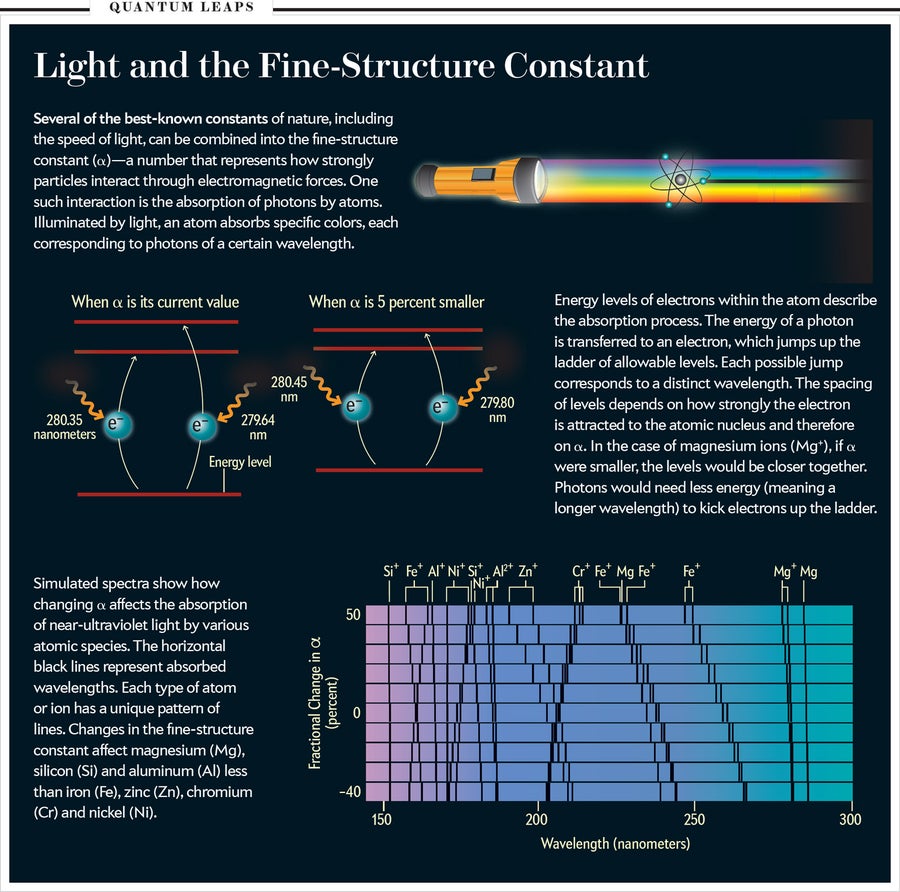
如果 α 具有不同的值，我们周围世界的所有重要特征都会发生变化。如果该值较低，固体原子物质的密度会下降（与 α³ 成正比），分子键会在较低温度下断裂（α²），并且元素周期表中稳定元素的数量可能会增加（1/α）。如果 α 太大，小原子核将无法存在，因为其质子的电斥力将压倒将它们结合在一起的强核力。像 0.1 这样大的值会炸裂碳。

恒星中的核反应对 α 尤其敏感。为了发生聚变，恒星的引力必须产生足够高的温度，以迫使原子核克服彼此排斥的趋势而聚集在一起。如果 α 超过 0.1，聚变将不可能发生（除非调整其他参数，例如电子与质子的质量比以进行补偿）。α 仅 4% 的变化就会将碳核中的能级改变到如此程度，以至于恒星产生这种元素的活动将停止。

核扩散

第二个实验问题，不太容易解决，是测量常数的变化需要高精度设备，该设备必须保持足够长时间的稳定以记录任何变化。即使是原子钟也只能在几天或最多几年的时间内检测到精细结构常数的漂移。如果 α 在三年多的时间内变化超过 10¹⁵ 分之四，最好的时钟也能看到它。但没有时钟看到。这听起来像是对常数性的令人印象深刻的证实，但三年在宇宙的时间尺度上只是眨眼一瞬间。在宇宙漫长的历史中，缓慢但实质性的变化会被忽视。

幸运的是，物理学家已经找到了其他测试方法。在 20 世纪 70 年代，法国原子能委员会的科学家注意到加蓬奥克洛铀矿的矿石同位素组成有些奇怪：它看起来像核反应堆的废料。大约 20 亿年前，奥克洛一定是天然反应堆的所在地。

1976 年，俄罗斯圣彼得堡核物理研究所和哈佛大学已故的亚历山大·什利亚赫特注意到，天然反应堆的运行能力关键取决于钐核特定状态的精确能量，该能量有助于中子的俘获。而该能量对 α 的值非常敏感。因此，如果精细结构常数略有不同，就不会发生链式反应。然而，链式反应确实发生了，这意味着在过去 20 亿年中，该常数的变化不超过 10⁸ 分之一。（物理学家继续争论确切的定量结果，因为天然反应堆内部的条件不可避免地存在不确定性。）

1962 年，普林斯顿大学的 P·詹姆斯·E·皮布尔斯和罗伯特·迪克首次将类似的原理应用于陨石：这些古老岩石中不同同位素放射性衰变产生的丰度比取决于 α。最敏感的约束涉及铼到锇的 β 衰变。根据明尼苏达大学的基思·奥利夫、不列颠哥伦比亚省维多利亚大学的马克西姆·波斯佩洛夫及其同事的工作，在岩石形成时，α 与其当前值的偏差在 10⁶ 分之二以内。该结果不如奥克洛数据精确，但时间更早，可追溯到 46 亿年前太阳系的起源。

为了探测更长时间跨度内可能发生的变化，研究人员必须仰望天空。光需要数十亿年才能从遥远的天文光源到达我们的望远镜。它携带着光线开始旅程或途中遇到物质时物理定律和常数的快照。

谱线编辑

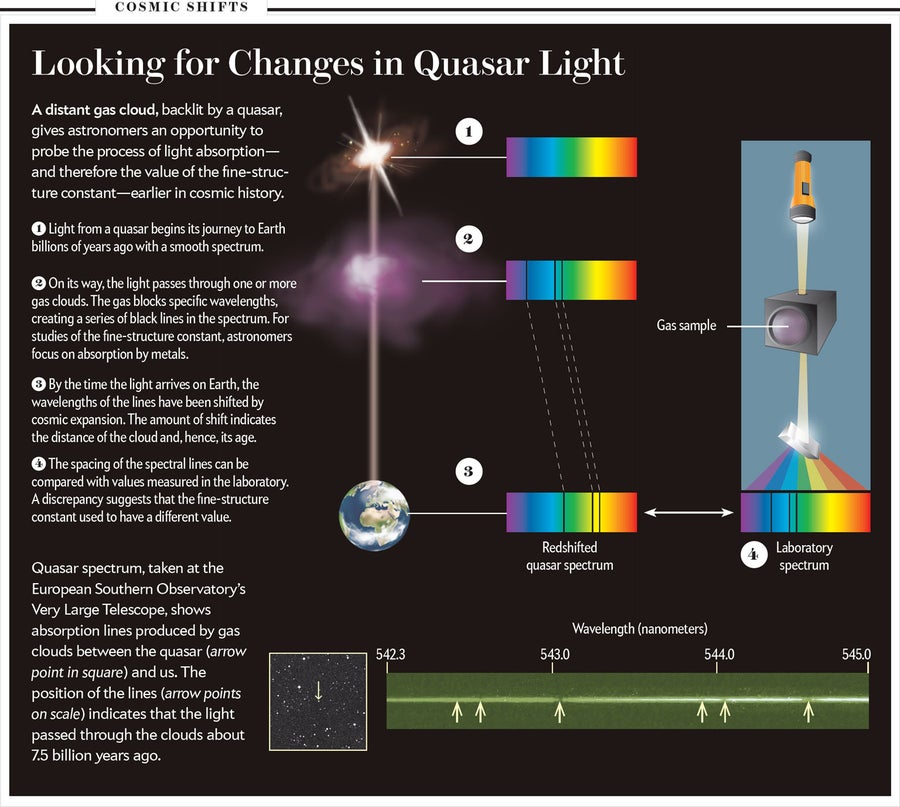
天文学在 1965 年类星体被发现后不久就进入了常数的故事。这个想法很简单。类星体刚刚被发现并被确定为位于距地球遥远距离的明亮光源。由于从类星体到我们的光路非常长，它不可避免地会与年轻星系的气态外围相交。气体在特定频率下吸收类星体光，从而在类星体光谱上印上一系列窄线的条形码[见上方框图]。

每当气体吸收光时，原子内的电子就会从低能态跃迁到高能态。这些能级由原子核束缚电子的紧密程度决定，这取决于它们之间电磁力的强度——因此也取决于精细结构常数。如果常数在光被吸收时或在宇宙中发生的特定区域不同，那么提升电子所需的能量将与今天实验室实验中所需的能量不同，并且光谱中看到的跃迁波长也会不同。波长变化的方式关键取决于电子的轨道构型。对于给定的 α 变化，一些波长会缩短，而另一些波长会增加。效果的复杂模式很难通过数据校准错误来模拟，这使得测试非常强大。

在我们二十年前开始这项工作之前，进行测量的尝试受到了两个限制。首先，实验室研究人员没有以足够的精度测量许多相关谱线的波长。具有讽刺意味的是，科学家过去对数十亿光年之外的类星体光谱的了解比对地球上样本光谱的了解还要多。我们需要一些高精度实验室测量值来与类星体光谱进行比较，因此我们说服实验人员进行这些测量。最初的测量由伦敦帝国学院的安妮·索恩和朱丽叶·皮克林完成，随后是由瑞典隆德天文台已故的斯韦内里克·约翰松、美国国家标准与技术研究院的乌尔夫·格里斯曼以及现在德国卡尔斯鲁厄理工学院的赖纳·克林领导的团队完成的。

第二个问题是，以前的观察者使用了所谓的碱金属双线吸收线——源自同一种气体（如碳或硅）的成对吸收线。他们将类星体光谱中这些线之间的间距与实验室测量值进行了比较。然而，这种方法未能利用一种特殊的现象：α 的变化不仅会改变原子能级相对于最低能级或基态的间距，还会改变基态本身的位置。事实上，第二种效应甚至比第一种效应更强。因此，观察者实现的最高精度仅约为 10⁴ 分之一。

1999 年，我们中的一位（韦伯）和悉尼新南威尔士大学的维克托·V·弗拉姆鲍姆提出了一种将这两种效应都考虑在内的方法。结果是一项突破：这意味着灵敏度提高了 10 倍。此外，该方法允许比较不同的物种（例如，镁和铁），这允许额外的交叉检查。将这个想法付诸实践需要复杂的数值计算，以精确确定所有不同原子类型中观察到的波长如何依赖于 α。结合现代望远镜和探测器，这种称为多重多重线方法的新方法使我们能够以前所未有的精度测试 α 的常数性。

改变观念

在开始这个项目时，我们预计会确定很久以前的精细结构常数值与今天的相同；我们的贡献仅仅是更高的精度。令我们惊讶的是，1999 年的第一个结果显示出微小但具有统计学意义的差异。进一步的数据证实了这一发现。基于总共 128 条类星体吸收线，我们发现在过去 60 亿到 120 亿年中，α 平均增加了接近百万分之六。

非凡的主张需要非凡的证据，因此我们立即想到数据或分析方法可能存在问题。这些不确定性可以分为两种类型：系统性和随机性。随机不确定性更容易理解；它们就是随机的。它们对于每次单独的测量都不同，但在大量样本中平均下来接近于零。系统性不确定性不会平均下来，因此更难处理。它们在天文学中是地方性的。实验室实验人员可以改变他们的仪器设置以最大限度地减少它们，但天文学家无法改变宇宙，因此他们不得不接受所有数据收集方法都存在不可消除的偏差。例如，任何星系调查都倾向于过度代表明亮的星系，因为它们更容易看到。识别和消除这些偏差是一个持续的挑战。

我们寻找的第一个偏差是波长刻度的失真，类星体光谱线是根据该刻度测量的。例如，在将类星体数据从望远镜的原始形式处理成校准光谱的过程中，可能会引入这种失真。尽管波长刻度的简单线性拉伸或压缩不能精确地模拟 α 的变化，但即使是不精确的模拟也可能足以解释我们的结果。为了测试此类问题，我们用校准数据代替类星体数据并对其进行分析，假装它们是类星体数据。该实验以很高的置信度排除了简单的失真误差。

两年多来，我们提出了一个又一个潜在的偏差，但在详细调查后才将其排除，认为其影响太小。到目前为止，我们只发现了一个潜在的严重偏差来源。它涉及元素镁产生的吸收线。镁的三种稳定同位素中的每一种都吸收不同波长的光，但这三个波长彼此非常接近，类星体光谱通常将这三条线混合在一起视为一条线。根据实验室对三种同位素相对丰度的测量，研究人员推断出每种同位素的贡献。如果年轻宇宙中的这些丰度差异很大——如果将镁倾泻到星系中的恒星平均而言比今天的恒星更重，则可能会发生这种情况——这些差异可能会模拟 α 的变化。

到 2010 年年中，我们完成了对欧洲南方天文台运行的甚大望远镜 (VLT) 大量新数据的分析，并获得了 153 个新的测量值。我们小组之前分析的所有数据都来自夏威夷莫纳克亚山的凯克望远镜。对于这些新的 VLT 数据，一切都不同——望远镜、光谱仪、探测器和用于数据分析初始阶段的软件。因此，这些 VLT 数据为我们从凯克望远镜获得的结果提供了完美的交叉检查。

我们认为新数据可能根本没有显示 α 的变化，或者它们会显示与凯克数据相同的效果——α 在更高的红移处显得更小。我们实际发现的情况确实令人震惊，如果正确的话，将彻底改变我们在物理学中最基本的一些概念。

新的 VLT 数据显示的不是高红移处 α 值更小，而是更大的值，比凯克数据小的值大约大相同的量。这怎么可能呢？我们立即想到的是，我们看到了两个数据集中都存在系统性问题的证据。将凯克和 VLT 样本加在一起，在良好的近似下，组合样本显示 α 随红移没有变化。问题解决了。常数毕竟真的是常数。

但如果这是解释，则需要两种不同的系统性效应，每种望远镜各一种，并且这两种效应都独立地具有相同的大小但符号相反。这并非不可能，尽管到目前为止我们尚未设法确定这对未知的系统性效应可能是什么。

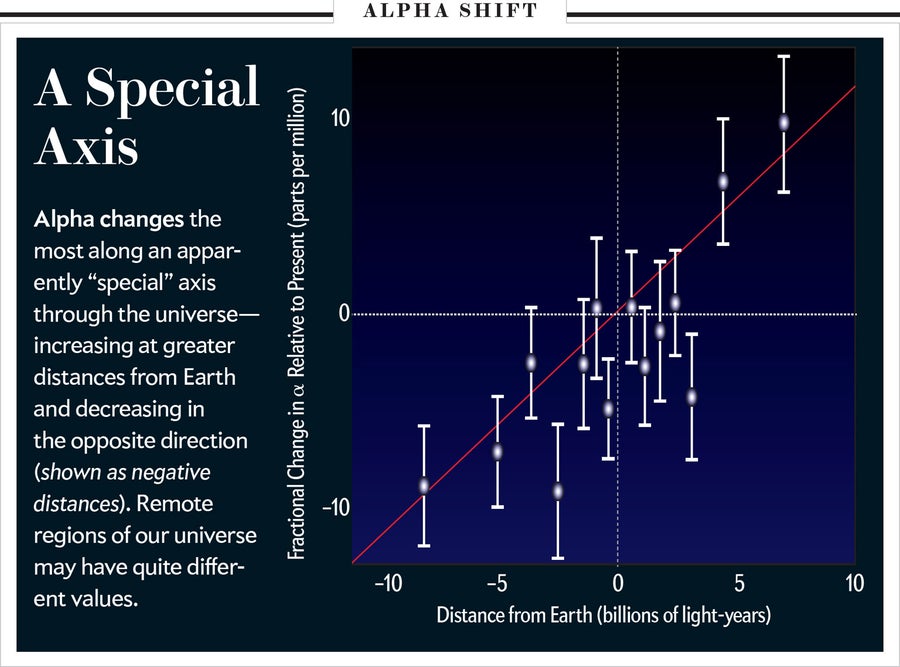
然而，我们发现了另一个奇怪之处。凯克数据覆盖了北半球天空的很大一部分，大到可以询问 α 的变化在该样本中是否存在任何“首选方向”。换句话说：α 的变化可能是随天空中的位置而不是随红移变化的吗？一个简单的分析确定了一个特定的方向，情况可能就是这样。令人惊讶的是，当独立分析 VLT 数据时，也出现了相同的方向。VLT 位于智利，平均而言，它指向的宇宙部分与凯克望远镜非常不同。又一个巧合？可能，但这现在使巧合变成了两个。

当我们合并旧的凯克和新的 VLT 样本时会发生什么？结果非常有趣：方向依赖性变得非常显着。偶然得出这样的结果似乎极不可能。如果结果是侥幸，我们可能会预期数据的子集会产生异常结果。考虑到这一点，我们设计了一个简单的测试来迭代减少样本，一次丢弃一个点，以查看我们需要消除多少数据才能使 α 明显的空间依赖性消失。我们发现我们需要丢弃一半的数据，机会概率才会降低到足够不令人印象深刻的水平！再说一次，这也许是侥幸。然而，尽管进行了广泛的尝试，我们尚未找到数据中可以模拟空间依赖性的系统性效应组合。Alpha 似乎在空间上发生变化——可能遍及整个可观测宇宙。任何随时间的变化都较小，并且目前低于我们的检测灵敏度。

改革定律

如果我们的发现被证明是正确的，那么后果将是巨大的，尽管只进行了部分探索。直到最近，所有评估精细结构常数变化时宇宙会发生什么情况的尝试都不尽如人意。它们无非是假设 α 在假设它是常数的情况下推导出的相同公式中变成了变量。这是一种可疑的做法。如果 α 变化，那么它的影响必须守恒能量和动量，并且它们必须影响宇宙中的引力场。1982 年，耶路撒冷希伯来大学的雅各布·D·贝肯斯坦首次推广了电磁学定律，以严格处理不恒定的常数。贝肯斯坦的理论将 α 从一个简单的数字提升为所谓的标量场，成为自然界的一个动态组成部分。然而，他的理论不包括引力。大约 20 年前，我们中的一位（巴罗）与伦敦帝国学院的若昂·马古伊若以及当时也在帝国学院的哈瓦德·B·桑德维克一起将其扩展到包括引力。

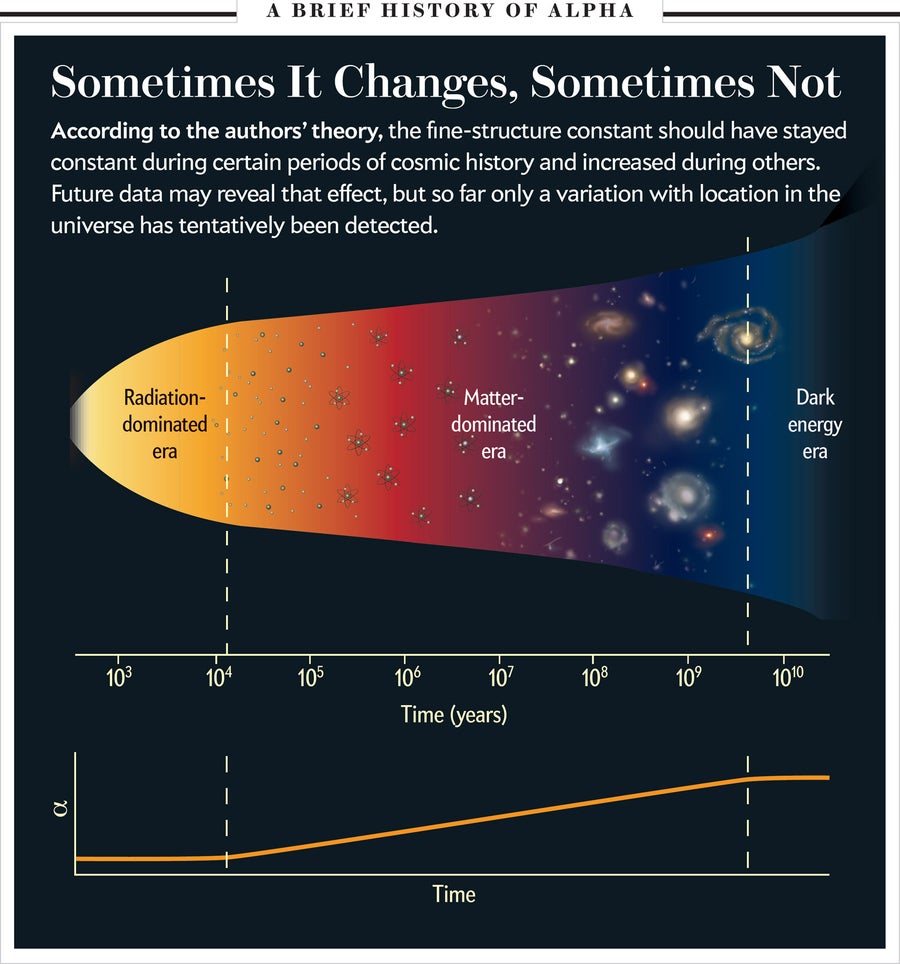
该理论做出了非常简单的预测。百万分之几的 α 变化应该对宇宙的膨胀产生完全可以忽略不计的影响。那是因为在宇宙尺度上，电磁学比引力弱得多。但是，尽管精细结构常数的变化不会显着影响宇宙的膨胀，但膨胀会影响 α。α 的变化是由电场能量和磁场能量之间的不平衡驱动的。在宇宙历史的最初几万年中，辐射超过了带电粒子，并使电场和磁场保持平衡。随着宇宙膨胀，辐射变稀薄，物质成为宇宙的主要成分。电能和磁能变得不相等，α 开始非常缓慢地增加，随着时间的对数增长。大约 60 亿年前，暗能量接管并加速了膨胀，使得所有物理影响都难以在空间中传播。因此，α 再次变得几乎恒定。

这种预测的模式与我们早期来自凯克望远镜的数据一致，这些数据似乎表明 α 的红移依赖性可能与时间变化有关。但是 VLT 数据给这项工作带来了很大的障碍。如果凯克数据是正确的，并且如果 VLT 数据也是正确的，即使时间变化确实发生，它也必须比我们现在可能看到的空间变化小。

Alpha 只是开始

任何值得考虑的理论都不仅仅是重现观测结果；它必须做出新的预测。上述理论表明，改变精细结构常数会使物体以不同的方式坠落。伽利略预测，真空中的物体以相同的速率坠落，无论它们由什么制成——这种想法被称为弱等效原理，当阿波罗 15 号宇航员大卫·斯科特扔下一根羽毛和一个锤子并看到它们同时撞击月球尘土时，这一原理得到了著名的证明。但是如果 α 变化，该原理就不再完全成立。这些变化会对所有带电粒子产生力。原子核中质子越多，它感受到的力就越强。如果我们的类星体观测是正确的，那么不同材料的加速度差异约为 10¹⁴ 分之一——对于实验室来说太小了，大约小 100 倍，但对于计划中的任务（如 STEP（等效原理的空间测试））来说足够大，可以显示出来。

那么，就 α 而言，这一系列活动将科学置于何处？我们和许多其他人渴望证实或证伪 α 在声称的水平上变化。有趣的是，新结果的延迟不是因为缺乏天文数据。凯克和 VLT 档案中已经包含大量等待分析的类星体光谱。欧洲南方天文台建造了一种名为 ESPRESSO 的新仪器，具有更高的校准精度，用于对早期宇宙中的 α 进行新的测量。

如果已经有大量数据可用，并且新的和更好的数据正在路上，那么我们还需要什么？现有的测量工作付出了巨大的努力和大量的时间。仅分析一个类星体光谱就非常耗时且复杂，需要相当多的专业知识，并且涉及人为的——即主观的——决策。为了解决这个瓶颈，我们中的一位（韦伯）与当时在新南威尔士大学的博士生马修·贝恩布里奇合作开发了一种新的人工智能程序，该程序能够对类星体光谱进行完全自动化的分析，产生的结果比人做同样的工作更客观和可重复。这种人工智能分析需要大量的计算，并且必须使用超级计算机。这项工作现在正在进行中，计算正在澳大利亚和英国的超级计算机上进行。

主要关注点是 α，而不是其他自然常数，仅仅是因为可以建立一个统计测量样本，更详细地绘制整个遥远宇宙的物理定律。然而，如果 α 容易发生变化，那么其他常数也应该发生变化，从而使自然界的内在运作比科学家曾经怀疑的更加变化无常。