第三方总统候选人经常被指责通过“窃取”主要政党的选票来破坏选举。但是,借助社会选择理论的数学,选举可以拥抱像拉尔夫·纳德这样的世界。
以2000年美国总统大选戈尔对布什的历史性胶着局面为例,当时美国人焦急地等待法律战的解决和重新计票,而重新计票在一个月内都不会揭晓获胜者。《洋葱报》当时发布了标题为“重新计票显示纳德击败”的新闻。当然,拉尔夫·纳德从来都不是有力的竞争者。这导致许多人认为,绿党候选人,像其他第三方政治家一样,从两大主要政党之一那里吸引了足够的选票,从而使天平向他们倾斜(在本例中是民主党人,他们仅以537票的差距输掉了选举)。
排序复选投票是一种替代选举制度,社会选择理论家认为,它可以减轻“剧透效应”,同时让选民在投票时有更多的发言权。排序复选投票具有一些明显的优势。然而,关于如何最好地实施它的数学讨论却出人意料地微妙。 而经济学中的一个古老定理表明,所有使用排序复选投票的尝试都容易受到违反直觉的结果的影响。
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业: 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和想法的具有影响力的故事。
排序复选投票允许人们按偏好顺序对候选人进行排序,而不是只投票给一位候选人。这样,如果有人想支持纳德,但又不想从戈尔那里夺走选票,他们可以在投票站将戈尔排在第二位。当纳德没有获得足够的选票时,戈尔的第二名排名仍然会在选举中使他受益。支持者还认为,排序复选投票会抑制恶意的诽谤竞选策略。这是因为,与典型的选举不同,排序复选投票中的候选人需要吸引所有选民,即使是那些不会在选票上给他们第一名的人。目前,缅因州和阿拉斯加州已对所有州和联邦选举实行排序复选投票,包括总统初选,在总统初选中,多位候选人更有可能吸引相同的选民。
一旦选民对候选人进行排序,如何汇总这些信息以揭示唯一的获胜者?答案并不像看起来那么简单,并且已经提出了许多方案。让我们探讨三种计票方法:简单多数制、即时决胜制和“孔多塞方法”,每种方法都会导致意想不到的行为。
与即时决胜制和孔多塞方法不同,简单多数制实际上并不是一种排序复选投票方案。事实上,它是美国最常见的投票方法:谁获得的第一选择票最多,谁就赢得选举。简单多数制可能会带来不利的结果。除了第三方选举搅局者的问题外,想象一下,如果候选人A获得34%的选票,而候选人B和C各获得33%的选票。即使候选人A是其他所有选民的最后选择,他也会以简单多数获胜。因此,66%的人口会选择他们最后选择的总统。简单多数制浪费选票,并忽略了选民偏好的全部范围。
一种更好的方法(也是美国实施排序复选投票以及奥斯卡金像奖最佳影片评选中使用的方法)称为即时决胜制。如果没有候选人获得超过一半的第一选择票,那么第一选择票最少的候选人将被排除在考虑范围之外,他们的选票将根据选民的下一个选择重新分配(例如,如果您的三位候选人排名是 1) B, 2) C, 3) A,并且候选人 C 因第一选择票最少而被移除,那么 A 将在您的选票中被提升以填补 C 的空缺:1) B, 2) A)。删除第一选择票最少的候选人的过程重复进行,直到一位候选人获得多数票。 虽然即时决胜制比简单多数制浪费的选票更少,但它也有自身的缺点。可能会出现奇怪的情况,即您最喜欢的候选人如果获得更多的第一选择票,反而更有可能输掉选举。
下图(基于 electionscience.org 的一个例子)描述了这种情况。在一个假设的即时决胜选举(称为选举 1)中,候选人 A 获胜。尽管 A 和 B 拥有相同数量的第一选择票,但两者都没有赢得选举所需的多数票(17 票中的 9 票)。因此,第一选择票最少的 C 被排除在竞争之外,并且调整选票以填补 C 的空缺,从而为候选人 A 赢得多数票。
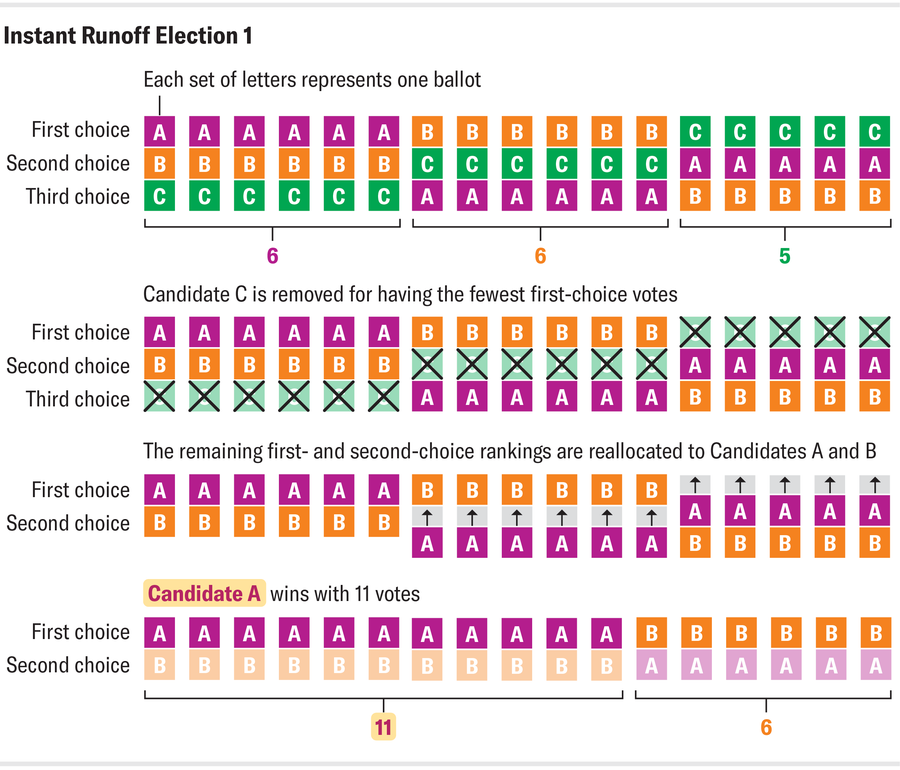
来源:Amanda Montañez;来源:https://electionscience.org/library/monotonicity/
现在想象一下另一种情况,称为选举 2,其中每个人都以与选举 1 相同的方式投票,除了两个人将 A 从他们的第三选择升级为第一选择。令人惊讶的是,即使 A 赢得了选举 1,并且现在比以前拥有更多的第一选择票,C 也成为了新的获胜者。这是因为升级 A 会导致 B 降级,因此 B 现在是第一选择票最少的候选人。当 B 被移除时,A 在与 C 的一对一较量中不如他们在选举 1 中与 B 的较量那样顺利。
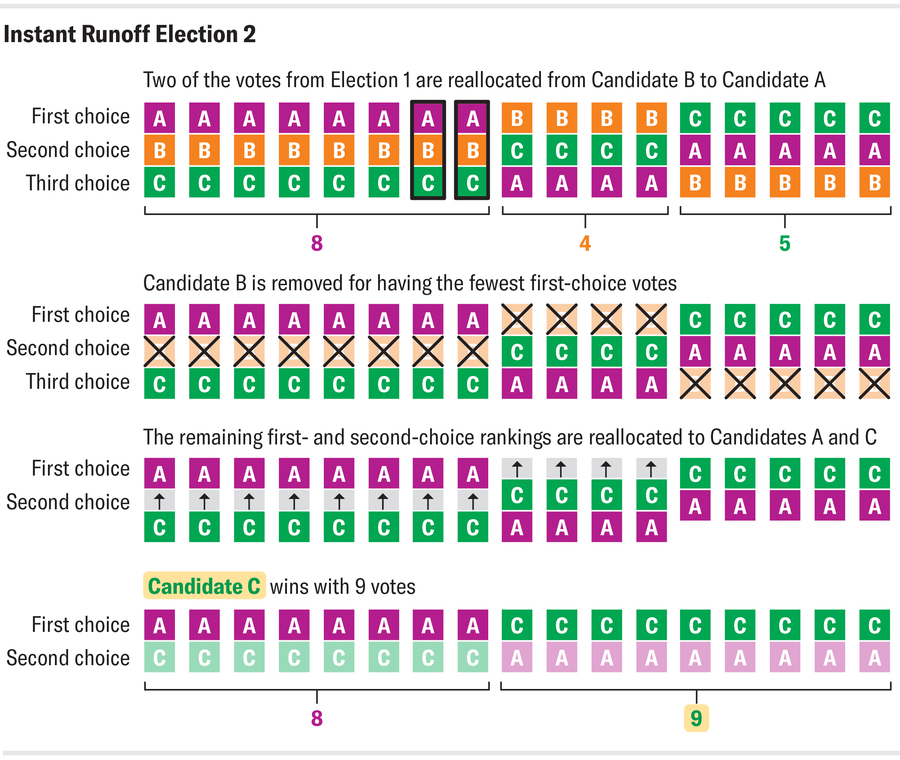
来源:Amanda Montañez;来源:https://electionscience.org/library/monotonicity/
这种违反直觉的现象发生在佛蒙特州伯灵顿市 2009 年的市长选举中,进步党成员鲍勃·基斯在即时决胜选举中击败了共和党和民主党提名人。令人惊讶的是,如果更多的选民将基斯放在他们的排名第一位,他就会输掉选举。
孔多塞方法,以 18 世纪法国数学家和政治哲学家孔多塞侯爵的名字命名,选出一位在与任何其他候选人的一对一选举中都会获胜的候选人。例如,假设在 2000 年没有任何第三方候选人的选举中,阿尔·戈尔本可以击败乔治·W·布什。戈尔当然也会在与任何一位第三方候选人的一对一竞争中获胜。戈尔赢得任何假设的一对一选举都将使他成为所谓的孔多塞候选人。看起来很明显,这样的候选人应该是胜利者,因为民众更喜欢他们而不是所有的对手。但是,在选举孔多塞候选人时,这里有一个重要的障碍:他们并非总是存在。选民的偏好可能是循环的,例如民众更喜欢 A 而不是 B,更喜欢 B 而不是 C,但也更喜欢 C 而不是 A。这种违反传递性的现象被称为孔多塞悖论(并且让人想起非传递骰子,我最近写过关于它的文章)。
已经提出了几种其他将排名选票合并为获胜者的方案。它们各有优缺点,更令人不安的是,选举结果可能完全取决于使用哪种制度。
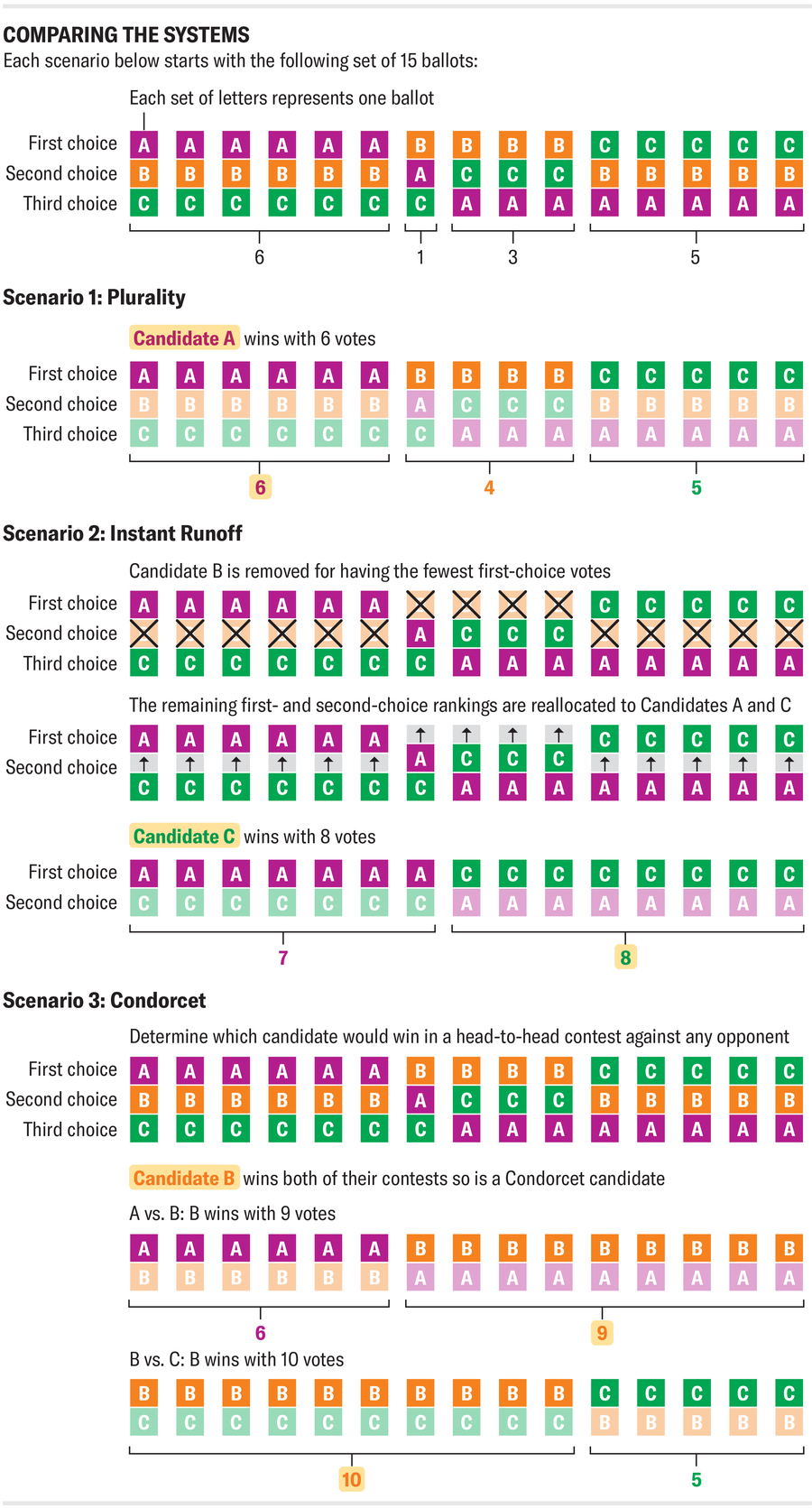
来源:Amanda Montañez
该图显示了一个简单的选举,在我们讨论的三种制度下产生了不同的结果。这种比较引出了一个充满希望的问题:是否存在完美的排序复选投票制度?也许我们只是尚未发现理想的设计,它可以在最大限度地代表公众利益的同时,避免现有提案的缺陷。诺贝尔经济学奖获得者肯尼斯·阿罗研究了这个问题,并提出了任何合理的聚合器(或将选民排名转换为一个社会排名的方法)的最低要求:
一致性:如果人口中的每个人都将候选人 A 排在候选人 B 之上,那么聚合器应将候选人 A 排在候选人 B 之上。
无关选项的独立性:假设聚合器将候选人 A 排在候选人 B 之上。如果选民要更改他们的一些排名,但每个人都保持他们对 A 与 B 的相对顺序不变,那么 A 在新的聚合排名中应保持在 B 之上。A 和 B 的社会排序应仅取决于 A 和 B 的个人排序,而不取决于其他候选人的排序。
这个常识性的清单设定了很低的门槛。但是阿罗证明了一个惊人的事实,这个事实后来被称为阿罗不可能定理:只有一种类型的聚合器可以同时满足这两个条件,那就是独裁统治。阿罗所说的独裁统治是指一个荒谬的聚合器,它总是简单地模仿同一个选民的排名。没有任何排序复选投票方案,无论它多么聪明或复杂,都可以在满足一致性和无关选项独立性的同时,除非它是独裁统治。该定理表明,没有完美的排序复选投票方案,我们总是不得不应对不良或违反直觉的结果。
这个证明并不意味着我们应该放弃排序复选投票。与简单多数制投票相比,它在捕捉选民意愿方面仍然做得更好。这仅仅意味着我们需要挑选并选择我们希望聚合器具有哪些属性,并承认我们不能拥有一切。该定理并没有说每次选举都会有缺陷,而是说没有哪种排序复选选举制度是不会出现缺陷的。阿罗曾评价他自己的结果:“大多数系统不会一直都很糟糕。我所证明的只是所有系统有时都可能很糟糕。”
我们中的理想主义者不应失去希望,因为排序复选投票并不是改进型选举制度的唯一选择。仅仅对候选人进行排名会丢失大量关于选民偏好的信息。例如,这是我对想吃的食物从最想要到最不想要的排名:香草冰淇淋 > 巧克力冰淇淋 > 我自己的运动鞋。排名没有传达出我对香草和巧克力冰淇淋的喜爱程度有多接近,也没有传达出我对我的耐克鞋有多厌恶。为了正确表达我的愿望,我应该给候选食物打分,以传达我不仅更喜欢哪些食物,而且喜欢多少。这被称为基数投票或范围投票,虽然它不是万能药,并且有其自身的缺点,但它规避了阿罗不可能定理的限制,该定理仅适用于排序复选投票。
我们都熟悉基数投票。在奥林匹克体操比赛中,评委通过给参赛者打出数字分数来决定获胜者,最终总分最高的人获胜。每当您在网上按消费者星级评分对产品进行排序时,您都会看到基数选举的获胜者。古代斯巴达人通过聚集在一个议会上,轮流为每位候选人呐喊来选举领导人。谁获得的呐喊声最大,谁就赢得了选举。虽然这在现代人听起来很粗糙,但这实际上是基数投票的早期形式。人们可以投票给多位候选人,并通过选择向人群的咆哮声贡献多少音量来“评分”。考虑到基数投票尽管比我们讨论过的任何其他制度都赋予了人民更多的发言权,但从未在现代选举中使用过,这令人印象深刻。也许我们不应该感到惊讶:毕竟,古希腊人确实发明了民主。
