研究人员利用量子“心灵感应”赢得“不可能”的游戏

要在桥牌纸牌游戏中获胜（由两组搭档进行），一名玩家必须以某种方式向队友示意他们手牌的强度。 心灵感应在这里会派上用场。 但是心灵感应不是真的，对吧？

这是正确的。 然而，几十年来，物理学家一直怀疑，如果桥牌是用受量子力学规则约束的纸牌进行，那么看起来非常像心灵感应的事情应该是可能的。 现在，中国的研究人员已经通过实验证明了这种所谓的量子伪心灵感应——不是在量子桥牌中，而是在一个名为 Mermin-Peres 魔方 (MPMS) 游戏的双人量子竞赛中，其中获胜要求玩家在不相互交换信息的情况下协调他们的行动。 如果运用得当，量子伪心灵感应可以让玩家赢得游戏的每一轮——这是原本不可能实现的完美表现。 这项使用激光光子进行的实验，探测了量子力学在允许粒子之间共享信息方面的极限。

印度马德拉斯理工学院的 Arul Lakshminarayan 说，这项工作“是对 Mermin-Peres 魔方游戏的一个美丽而简单的直接实现”，他没有参与实验演示。 他补充说，它的美部分来自于它优雅地证实了量子系统的状态在实际测量之前没有明确定义——这通常被认为是量子力学最令人困惑的特征。 “这些量子游戏严重破坏了我们关于物体具有通过观察揭示的预先存在属性的共同概念，”他说。

支持科学新闻报道

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道： 订阅。 通过购买订阅，您正在帮助确保未来能够继续报道关于塑造我们今天世界的发现和想法的具有影响力的故事。

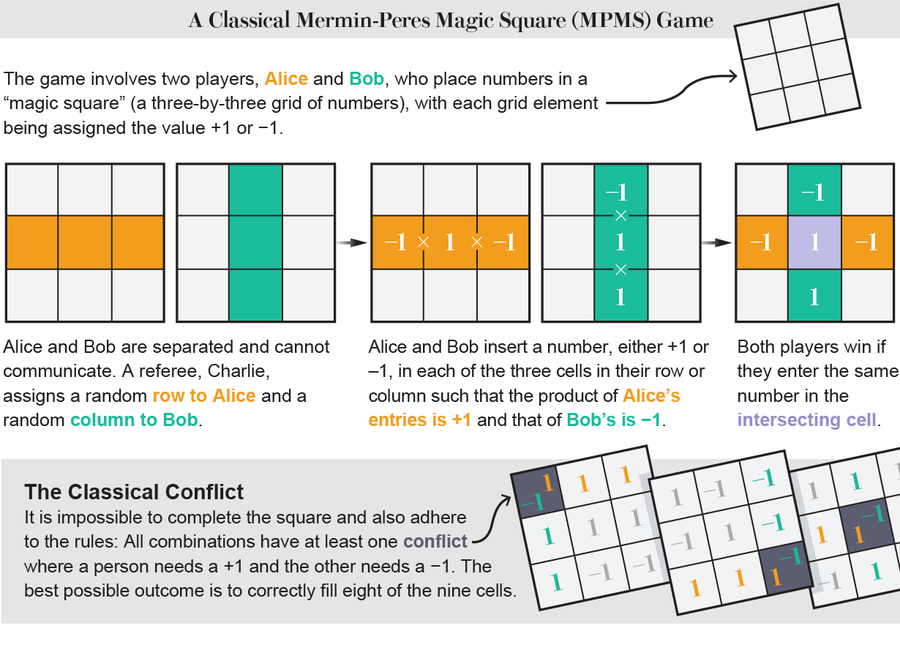
两位量子物理学家 Asher Peres 和 David Mermin 在 1990 年独立设计了 MPMS。 它涉及两名玩家（按照量子力学思想实验的传统，称为 Alice 和 Bob），他们必须填写一个“魔方”——一个三乘三的数字网格——每个网格元素都被分配一个 +1 或 -1 的值。 在每一轮中，裁判（Charlie）随机发送一行给 Alice，随后发送一列给 Bob（总共有九种这样的行和列组合）。 玩家必须告诉 Charlie 在他们的三个网格空格中放入哪些 +1 或 -1 的值。 与任何魔方挑战（例如数独）一样，每行和每列的总和必须满足特定的约束：这里，一行中所有条目的乘积必须等于 +1，而所有列的乘积必须为 -1。 如果 Alice 和 Bob 都为列和行重叠的网格元素分配相同的值，则他们赢得一轮。

经典上，不可能赢得所有轮次，因为即使 Alice 和 Bob 每次都猜得很好，但对于每个完成的方格，都不可避免地有一轮他们的分配必须冲突。 他们能做的最好的就是每九轮赢得八轮。

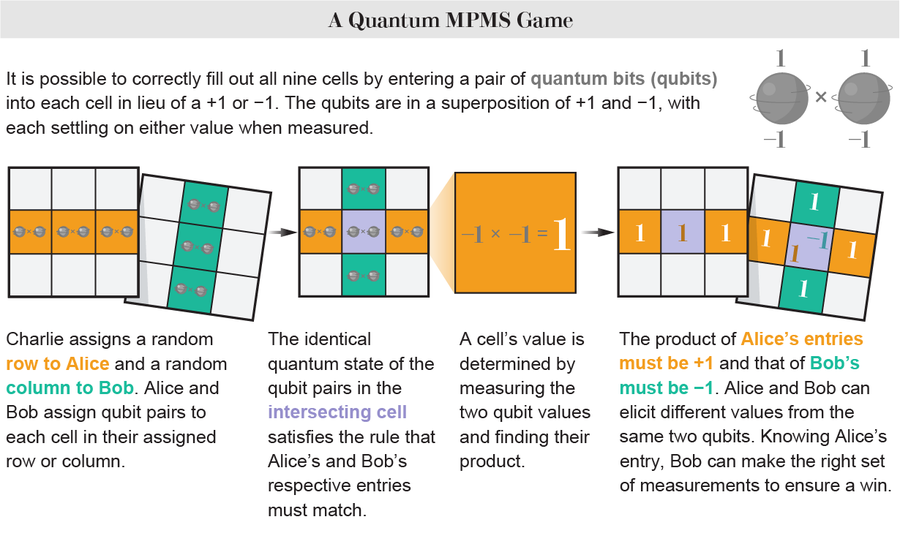
但是现在假设 Alice 和 Bob 可以使用这种量子策略：他们不是为每个网格元素分配 +1 或 -1 的值，而是为其分配一对量子比特（qubit），每个量子比特在测量时都有 +1 或 -1 的值。 每个玩家给特定网格元素的值是通过测量两个量子比特值并找到这对量子比特的乘积来确定的。 现在可以避免经典的冲突，因为 Alice 和 Bob 可以根据他们进行测量的方式从相同的两个量子比特中获得不同的值。 有一种特定的测量策略可以确保任何给定轮次的获胜标准——Alice 和 Bob 的三个条目的乘积分别为 +1 和 -1——在行和列的所有九种排列中都得到满足。

然而，这种策略存在一个问题。 为了进行正确的一组测量，Alice 和 Bob 需要知道他们的三个网格元素中哪一个是与另一位玩家的网格元素重叠的——他们需要协调。 但在 MPMS 中，这不是问题，因为他们对相同的三个量子比特对进行顺序测量。 这意味着到达 Bob 的量子比特对具有 Alice 已经如何测量这些量子比特的印记：他们可以相互传递信息。

1993 年，Mermin 表明 MPMS 可用于演示一种称为上下文性的量子现象。 上下文性最初由北爱尔兰物理学家 John Stewart Bell 于 1966 年提出，指的是量子测量的结果可能取决于测量方式。 系统中的一组经典测量将给出相同的结果，无论这些测量以什么顺序执行。 但对于量子测量，情况并非总是如此。 在 MPMS 中，上下文性源于这样一个事实：给定量子比特对的测量结果可能因同时测量的其他两个量子比特对而异。

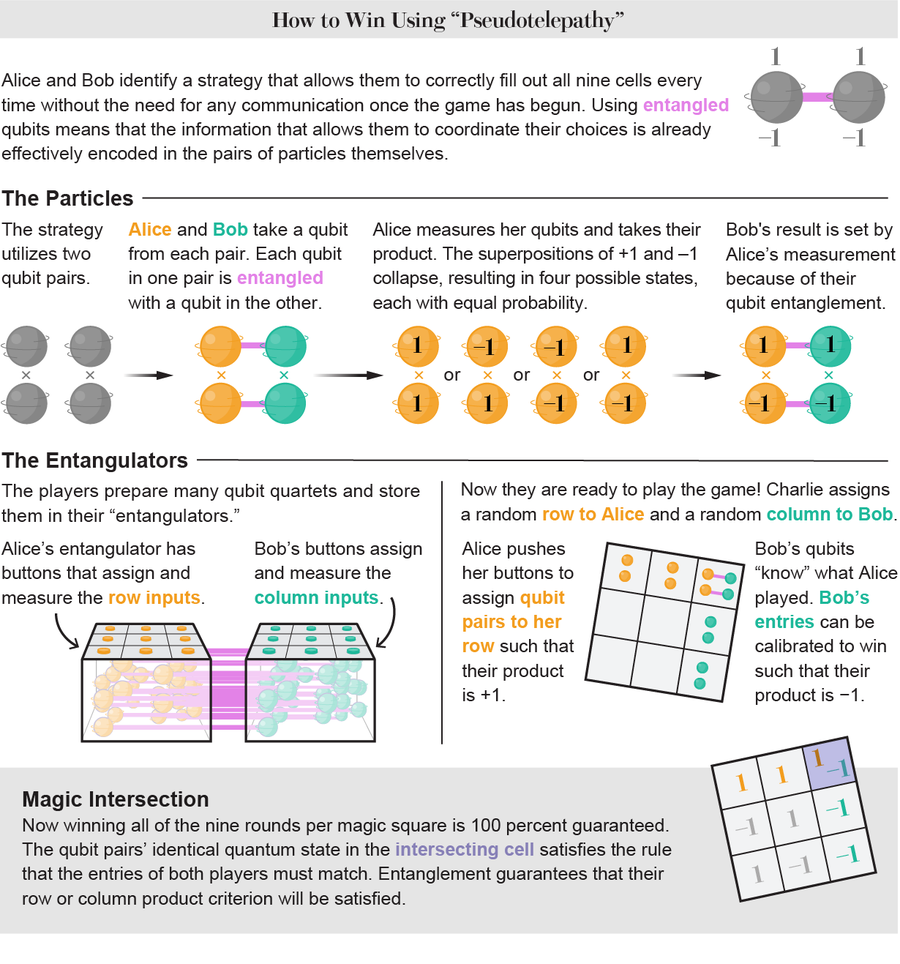
但是，如果我们禁止 MPMS 中的任何通信，方法是为 Alice 和 Bob 分配不同的量子比特对，并说他们不能商量如何测量它们，那会怎么样？ 那么，只有当每个玩家对另一位玩家所做的事情做出正确的猜测时，他们才能保证九轮全胜。 但在 2005 年发表的一项研究中，蒙特利尔大学的量子理论家 Gilles Brassard 及其同事表明，即使不进行通信，玩家也可以使用他们所谓的量子伪心灵感应，利用量子原理来保证每轮都获胜。

这种策略涉及将发送给 Alice 或 Bob 的每对量子比特中的一个量子比特与另一位玩家使用的相应量子比特纠缠在一起。 纠缠粒子具有相关的属性，因此如果 Alice 测量了她的粒子的值，那么 Bob 的粒子的值也会被固定下来。 两个纠缠的量子比特粒子可能是反相关的，这样如果发现 Alice 的量子比特的值为 +1，则 Bob 的量子比特的值必须为 -1。 在测量之前，无法知道 Alice 的量子比特具有哪个值——它可能是 +1 或 -1。 但 Bob 的量子比特将始终与其相反。 更重要的是，粒子对之间纠缠的属性被称为“非局域性”，这意味着它不是“局域”于任何一个粒子，而是在两者之间共享。 即使粒子相隔遥远，纠缠对也必须被视为一个单一的、非局域的对象。 2001 年，西班牙塞维利亚大学的量子理论家 Adán Cabello 在他称之为“all or nothing”的游戏中提出了赢得量子游戏的相同基本思想，后来证明该游戏等同于非局域（伪心灵感应）MPMS。

一些研究人员认为纠缠是量子力学最基本的方面。 它暗示了粒子之间的一种信息共享。 这是利用纠缠进行量子伪心灵感应的关键：Alice 和 Bob 不必交换信息来协调他们的行动，因为必要的信息已经共享在粒子对本身中。

上下文性和非局域性都提供了“量子资源”，可用于获得相对于经典信息处理方法的一些优势。 例如，在量子计算中，量子比特之间的纠缠通常是创建经典计算机无法获得的解决问题的捷径的资源。

物理学家已经使用纠缠光子在现实世界中反复演示了 Cabello 的全有或全无游戏。 但是，虽然这些实验确立了纠缠如何通过击败经典性能来传达“量子优势”，但中国科学技术大学的陈凯、中国南京大学的王锡林及其同事设计了一项新的实验，他们说该实验实现了完整的协议，以实现每轮都保证获胜——真正的、一致的量子伪心灵感应。

理想情况下，Alice 和 Bob 会在游戏开始前准备多组四个量子比特，每组四量子比特包含两对纠缠对。 Alice 会得到每对量子比特中的一个，Bob 会收到另一个。 然而，研究人员表示，为游戏的每一轮制作两对纠缠光子极具挑战性。 首先，在他们的设备中，即使产生一对纠缠对的概率也很低，因此一次制作两对的可能性极低。 而且，正如伪心灵感应 MPMS 所要求的那样，对于这种光学实现来说，同时检测两对量子比特对几乎是不可能的。

相反，陈、王及其同事制备了单光子对，并独立地纠缠了它们的两个属性：它们的偏振态和称为轨道角动量的属性。 光子包含在持续时间仅为 150 飞秒的超短激光脉冲中，并通过穿过两个所谓的非线性光学晶体而发生纠缠。 一块薄薄的硼酸钡板首先将一个单光子分裂成两个能量较低且具有相关角动量的光子。 然后，它们也通过偏振进行纠缠，方法是将其发送通过钇钒化合物的晶体。

为了证明接近 100% 的成功率，研究人员需要提高他们的检测效率，以便几乎没有纠缠光子在未被发现的情况下逃脱。 即使这样，在实验中也无法精确达到理论极限——但研究人员能够证明，他们可以以 91.5% 到 97% 的概率赢得每一轮。 这个范围转化为在总共进行的 1,075,930 轮比赛中，可靠地击败了经典八胜一负的限制，共计 1,009,610 轮。

陈说，伪心灵感应 MPMS 游戏利用了量子力学可能提供的粒子之间最强的相关程度。 “我们的实验探索了如何在粒子之间产生极端的量子相关性，”他说。 如果这些相关性再强一些，它们将暗示超光速信息交换，而许多其他独立实验表明这是不可能的。

Mermin 说，虽然实验结果令人印象深刻，但这种成功并没有揭示任何超出量子力学按我们想象的那样运作的事实。 Cabello 并不完全同意。 他说，除了是一场实验性的技术壮举之外，这项工作还展示了量子规则通过同时调动两个量子优势来源而使之成为可能的新变化：一个与非局域性相关，另一个与上下文性相关。 Cabello 说，同时研究这两种效应应该让物理学家能够更严格地探索它们之间的联系。

更重要的是，原则上，这些资源中的每一个都可以用于量子处理中的不同用途，从而提高其多功能性。 “例如，非局域性可以用于秘密通信[使用量子密码术]，而上下文性可以用于量子计算，”Cabello 说。 在这种情况下，例如，Bob 可以与 Alice 建立安全通信，同时与 Charlie 进行比经典方法允许的更快的计算。

Lakshminarayan 说，在这些实验中使用共享纠缠“导致了在经典上看起来很神奇的效果”。 但是，鉴于量子力学经常被误用作为伪科学主张的虚假理由，将这种现象称为“伪心灵感应”是否会自找麻烦？ Mermin 说，这是一个“邀请荒谬解释的糟糕术语”。 但虽然 Cabello 同意，但他承认，引人入胜的名字可以帮助宣传这种现象的趣味性。 “我们不要自欺欺人，”他说。 “可能正是由于‘伪心灵感应’这个词，[你和我]才正在进行这次对话。”