想象一下,您正在为六位客人举办一个小聚会,但不清楚谁认识谁,谁不认识谁。 事实证明,必然至少有三个人彼此完全陌生,或者至少有三个人已经是朋友。(我们并非假设您的朋友不喜欢彼此。)因此,总是会至少有一组三个人,他们彼此都认识或完全不认识。
乍一看,这听起来可能并不太令人惊讶,但您越思考这个问题,它就越有趣。 六个人彼此之间有 15 个联系。 因此,您可能会问,A 如何与 B 相关? A 如何与 C 相关? B 认识 C 吗? 这些联系可以有两个值之一:朋友或陌生人。 这意味着,仅有六位客人,就已经有 215 (32,768) 种不同的方式让聚会参与者彼此联系。 而数学主张,在每一种可能的分组中,总是有一个三人组,其中所有人都彼此认识,或者都是完全的陌生人。 逐个案例地查找三人组似乎相当麻烦。
事实上,弄清楚这一点属于拉姆齐理论的范畴,该理论以英国数学家弗兰克·拉姆齐(Frank Ramsey,1903-1930)的名字命名,他于 26 岁时不幸英年早逝。 然而,在他短暂的一生中,他成功地发展了一个数学分支,该分支处理识别混乱中的某种秩序。 其目的是在令人困惑的排列中识别重复出现的模式,就像我们聚会参与者的情况一样。 可以从数学的角度提出问题:您必须邀请多少位客人,才能至少有一组三个人彼此都认识,或者至少有一组三个人完全陌生?
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。 通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的具有影响力的故事。
整个事情可以用图形或图表来解决,这些图形或图表是点(也称为节点)和边(连接点的线)的网络。 每个人都象征着一个节点。 六位客人可以围成一个圆圈排列。 现在每个点都已连接。 这就产生了 15 条边。 根据两个人是否彼此认识,它们被涂成红色(表示熟人)或蓝色(表示陌生人)。 现在声明:无论您如何为边着色,您总是会得到一个单色三角形——一个全蓝色或全红色的图形。
现在拉姆齐理论提出的附加声明:对于刚才提到的六位客人,无论您如何为边着色,您总是会得到至少一个单色三角形——一个全蓝色或全红色的图形。 如果您尝试一下,您会看到这样的三角形总是会出现。
当然,没有人愿意浏览 32,768 种可能性。 这样做也不会回答拉姆齐提出的一个问题,即六是否是不可避免地形成这样一个三角形的最小客人人数。 您可以尝试通过更改邀请人数来解决这个问题。 如果您找到以某种方式着色的三角形,使得根本没有出现单色三角形,那么您就找到了相反的证据。 如果您只邀请三位客人,其中两个人可能之前见过面。 因此,在这种情况下,没有三个人是彼此都认识或彼此陌生的——因此没有单色三角形。
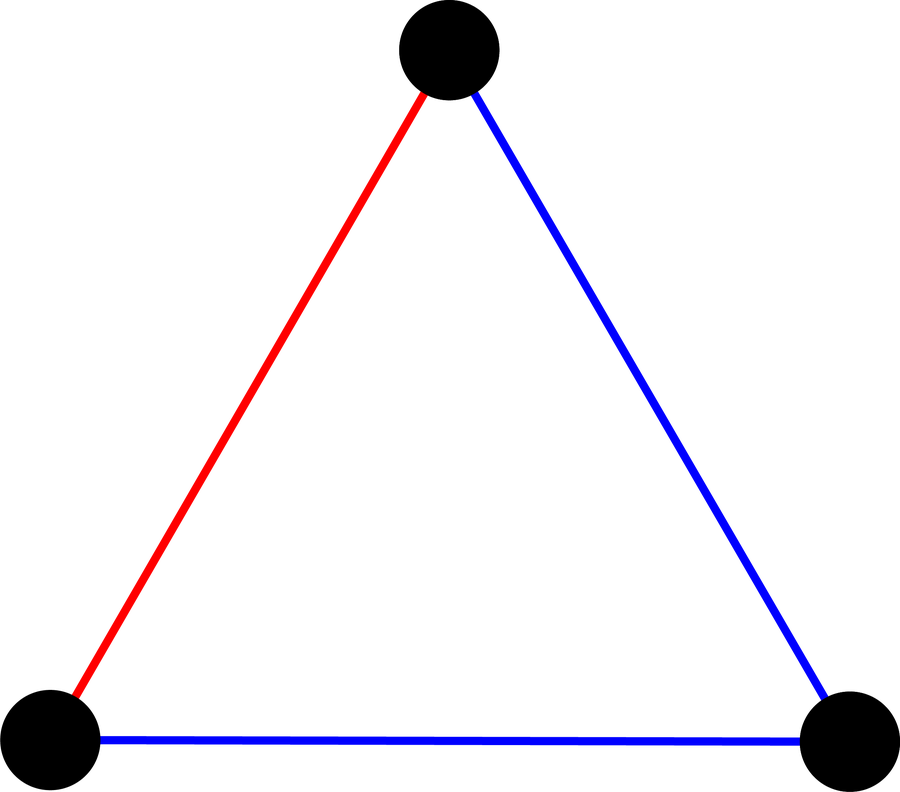
对于四个人来说,也很容易找到没有一组三个人彼此不认识或彼此是朋友的情况。
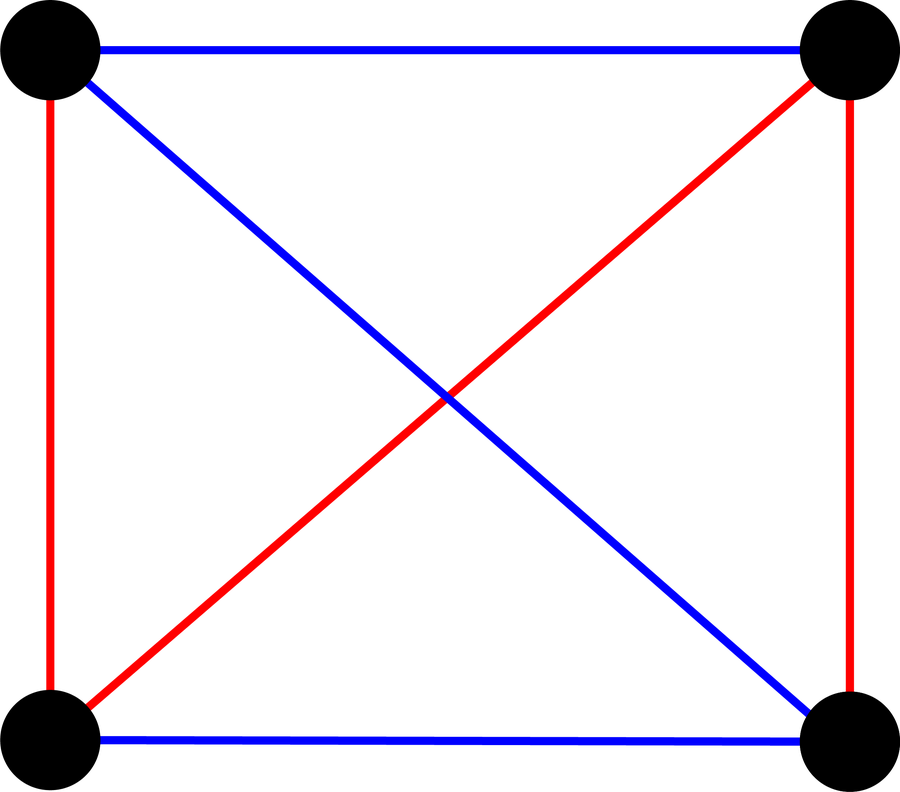
即使有五位客人,也至少有一种朋友-陌生人连接的配置,而没有相同颜色的三角形。 因此,要回答拉姆齐关于最小的聚会参与者群体的问题,他们的关系总是可以用至少一个单色三角形来描绘,这个数字必须大于五。 但要大多少呢?
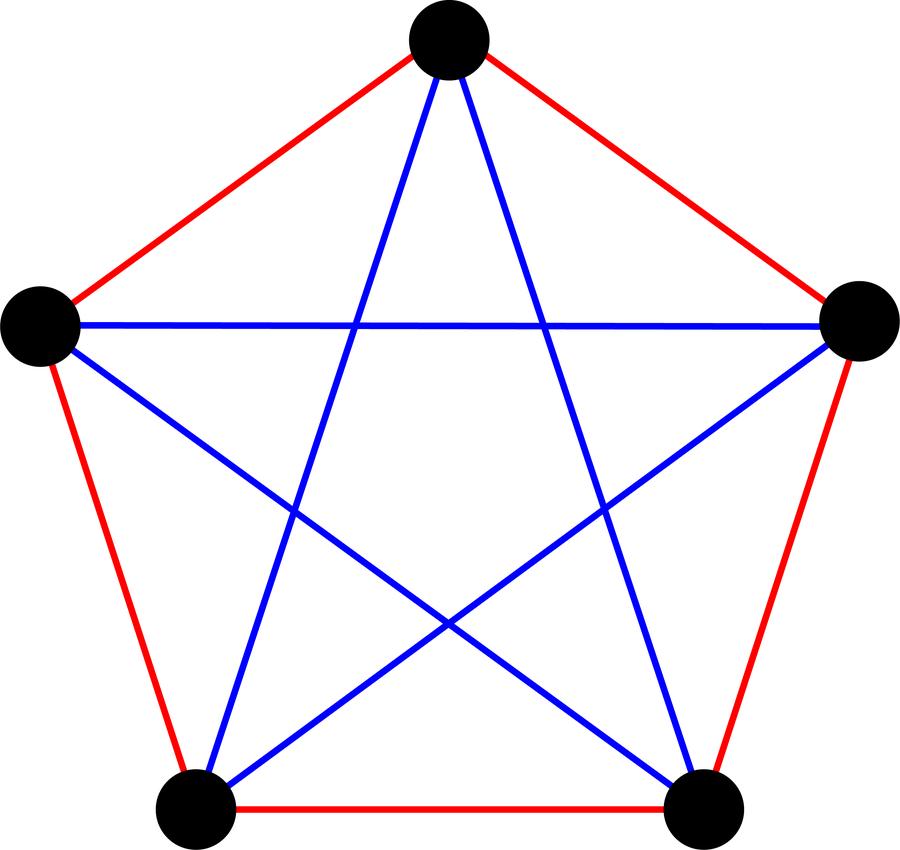
当我们达到六个人时会发生什么? 您现在必须尝试为图表的边着色,而不创建单色三角形。为此,您可以首先挑选出一个人 A,并检查他们与其余客人的关系可能是什么。 假设 A 是聚会的女主人。 在受邀者中,她有多少朋友? 有六种不同的方式将她与五位客人联系起来:例如,她可能没有朋友,在这种情况下,五位受邀者都对她来说是陌生人。 或者她可能有一位朋友,在这种情况下,有四位陌生人。 此图表显示了六位聚会参与者可能与女主人联系的各种方式。
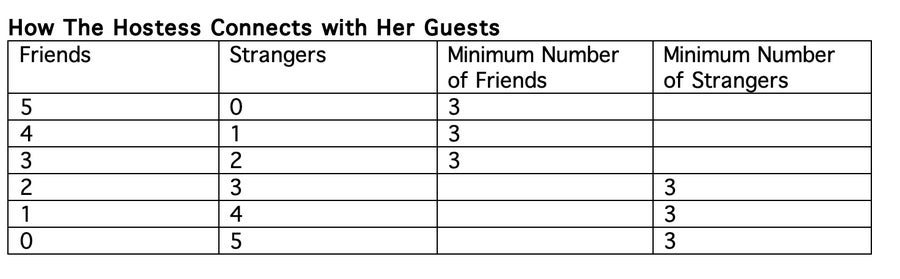
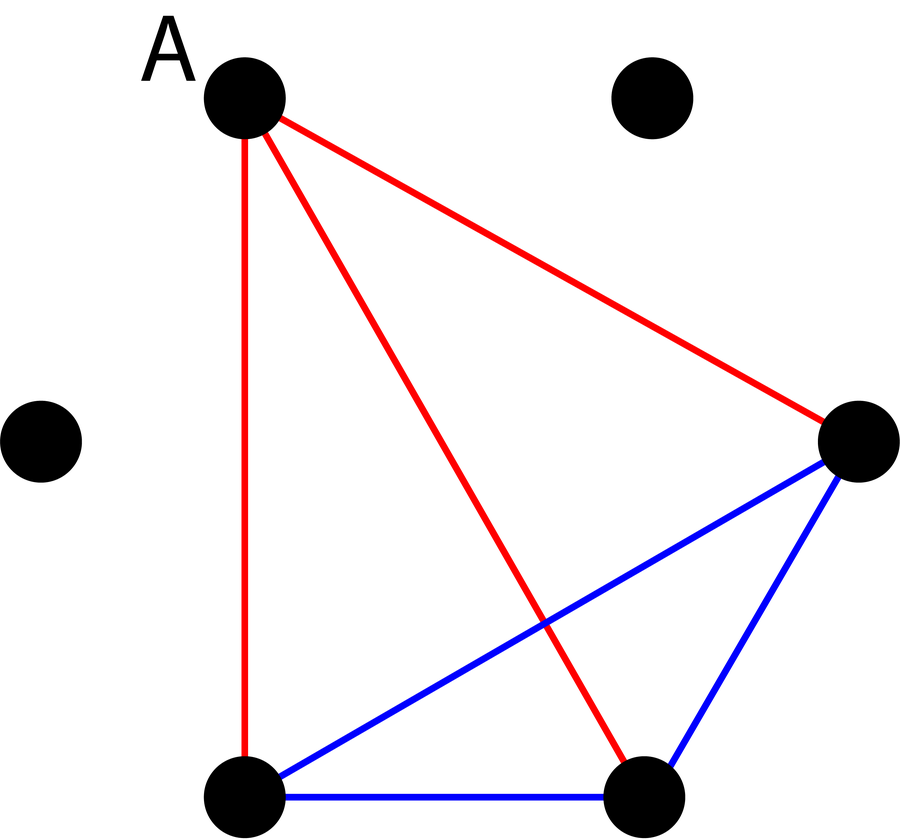
女主人(A)至少与三个人是朋友——或者至少有三个人对她来说是陌生的。 在图表中,可以通过她总是至少有三条相同颜色的边来看出这一点。 使用一个具体的例子,可以假设,在表中显示的配置之一中,女主人有三条红色边,这意味着她认识其他三位客人。 现在您可以尝试为剩余的连接着色,以避免在 32,768 种可能的着色组合中出现红色三角形。

因此,您必须确保任何两个认识女主人的客人彼此不认识——他们之间必须有蓝色连接。 但是,如果您将所有这些边都标记为蓝色,您将得到一个蓝色三角形! 也就是说,如果所有节点都必须连接,则无法避免六点图中的单色三角形。 而且您可以在所有点都连接的任何更大的图中找到这样的三角形。 这意味着,只要您邀请超过五位客人,就总会有一组三个人彼此都认识或彼此都不认识。
当然,数学家不会满足于单一的结果。 相反,他们试图概括问题。 因此,为了推导出拉姆齐数的一般情况,他们会问:“R 需要多少个最少节点才能总是找到红色 m-团或蓝色 n-团。 n-团表示一组彼此全部连接的 n 个点。 结果数 R(m,n) 称为拉姆齐数。 令人惊讶的是,已知的拉姆齐数非常少。 我们刚刚证明了 R(3,3) = 6。 也可以证明 R(4,4) = 18。 这意味着,如果您邀请 18 位客人参加聚会,则总会有一组四个人彼此都认识或彼此都不认识。
然而,几十年来,R(5,5) 有多大一直不清楚。 换句话说,您必须邀请多少位客人才能总是有一个五人组,他们要么都是熟人,要么都是陌生人? 专家们已经能够缩小结果范围:我们现在知道 R(5,5) 落在小于或等于 43 个节点的下限和小于或等于 48个节点的上限的范围内。似乎我们可以简单地使用计算机来遍历具有 43 个节点的图的所有可能的着色,看看是否存在一个不包含五个相同颜色组的图。 但事实上,这项任务超出了任何可用的计算能力!
一个具有 43 个节点且全部连接的图有 903 条边。 这些边可以是红色(朋友)或蓝色(陌生人)。 这就是 2903 种可能性,四舍五入约为 10272 。 这是一个 1 后面跟着 272 个零,这是难以想象的巨大数字。 为了理解它有多大,可以这样想:目前假设我们的宇宙由大约 1082 个原子组成。
假设每个原子都是一台计算机器,它每秒可以执行与目前最强大的超级计算机一样多的计算次数:每秒一百万兆(1018)步计算。 假设每个原子每秒可以搜索一百万兆个图,以查找五个一组的图——并且粒子会在 138 亿年前的大爆炸之后立即开始这样做。 那么到目前为止,他们将有 13.8 x 109 x 365.25 x 24 x 3,600 ≈ 4.35 x 1017 秒的时间来完成这项任务。 也就是说,宇宙中的所有原子到目前为止已经检查了大约 4.35 x 10117 个图——仅占剩余要处理的一小部分。
因此,数学家们正在寻找更聪明的解决方案来解决这个问题。 然而,到目前为止,他们还没有找到任何解决方案。
本文最初发表于 Spektrum der Wissenschaft ,经许可转载。
