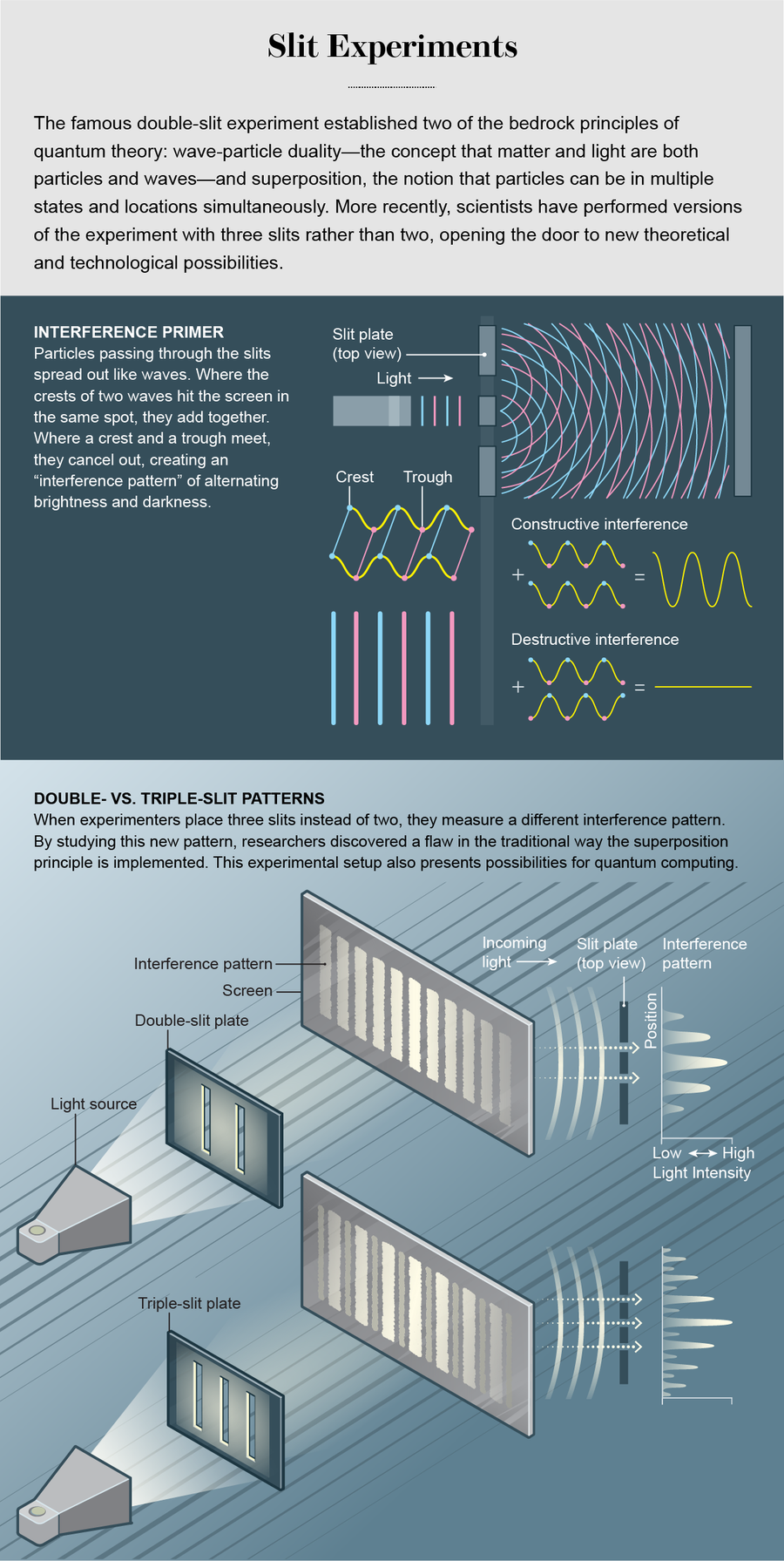
“量子力学的所有奥秘”都包含在双缝实验中,诺贝尔奖得主理查德·费曼曾说过一句名言。在1801年由英国博学家托马斯·杨首次提出的实验中,一束光子——光粒子——飞向一面墙,墙上切有两个狭缝。当光到达墙后的屏幕时,它会产生明显的“干涉图案”:明暗相间的条纹。只有当光子表现得像波而不是像点粒子时,才会出现这种图案,并且通过两个狭缝的波的波峰和波谷相互干涉,有时会增加光,有时会抵消光。当杨使用改进的装置进行实验时,这似乎确立了光是一种波而不是粒子。
真的是这样吗?奇怪的是,在几个世纪后的实验中,研究人员小心地一次只向墙壁照射一个光子,干涉图案仍然存在,就像单个粒子在与自身干涉一样。更奇怪的是,如果你在狭缝旁放置一个探测器来记录每个粒子通过哪个狭缝,干涉图案就会消失。取而代之的是,你在屏幕上得到两条光线,这正是你期望的点粒子而不是波通过时会得到的结果——就好像测量行为改变了粒子的性质一样。
时至今日,双缝实验以其概念的内在简洁性,仍然是进行过的最有趣的实验之一。它已经被重复了很多次,使用光和物质的粒子。它清楚地展示了量子力学的基本奇异性:光和物质实际上既是粒子又是波——这个概念被称为波粒二象性。它还确立了叠加原理:粒子可以存在于多种状态,甚至同时存在于多个位置。在双缝实验中,粒子一定不能只通过一个狭缝或另一个狭缝——为了发生干涉,每个粒子都必须通过两个狭缝。
支持科学新闻事业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的有影响力的故事的未来。
尽管这个实验广受赞誉,但我们尚未探究其深度。最近,我在印度班加罗尔拉曼研究所量子信息与计算实验室的团队,已经在微波波长范围内设置了“三缝”实验——我们使用三个狭缝而不是两个狭缝。这似乎是一个简单的调整,但它具有深远的意义。在理论方面,我们的三缝试验已经阐明了叠加原理在这种情况下如何应用,并揭示了我们对这种现象的基本理解中的新细微之处。
我们的三缝实验架构还在新兴的量子计算领域提供了有趣的机会。量子计算机有望实现以前难以处理的计算——如果我们能够利用量子物理学的力量来构建它们。量子计算的核心挑战之一是找到一种方法来增加量子计算机包含的比特数(称为量子比特),而不会破坏允许量子比特同时处于两种状态的叠加态——这是实现计算速度巨大提升的关键。当社区中的大多数人都在致力于增加系统中量子比特的数量时,我的实验室正在尝试一种替代的、较少探索的方法,即使用更高维度的“量子数字”而不是二维量子比特。使用三缝系统,我们可以创建称为三元量子比特的三维量子数字。
图片来源:尼克·博克尔曼
叠加原理
量子理论不仅将基本粒子描述为物理波,而且还描述为由所谓的波动方程决定的,其解可以用希腊字母psi,Ψ表示。这些解表示粒子处于任何特定状态的概率幅度。
然而,我们的研究揭示了物理学家在将波动方程计算应用于双缝实验时,传统处理方式中的一个缺陷。想象一下经典的实验,让两个狭缝分别命名为A和B。描述该系统中粒子的波动方程的解,当狭缝A打开时可以标记为ΨA,当狭缝B打开时可以标记为ΨB。当两个狭缝都打开时会发生什么?教科书中的常见做法是将解称为ΨA + ΨB,以表示粒子处于叠加态,其中它同时通过两个狭缝。这确实是叠加原理的应用,尽管是不完整的。原因很简单:两个狭缝同时打开的情况与分别打开狭缝的组合不同。我们知道,当它们同时打开时,粒子在某种程度上会同时通过两个狭缝并与自身相互作用,而我们不能简单地通过将两个解相加来表示这些相互作用。
科学家们之前已经提出,可能需要一些修正项来使我们的方程准确。这个量被称为索尔金参数,因为它是由当时在雪城大学的物理学家拉斐尔·索尔金在1994年预测的。然而,大多数研究人员都认为这个项会非常小,以至于可以忽略不计。事实上,我们知道它不能太大,否则早就应该被观察到了。但是我们的三缝实验证明,这个项确实存在,并且并非总是小到可以忽略不计。使用三个或更多狭缝为我们提供了这个修正项的天然试验平台,因为我们可以测量一个量(索尔金参数),如果修正项不存在,则该量将为零,如果它存在,则该量将为非零。(在双缝情况下,修正项被添加到已经非零的量中,因此它不会以明显的方式显示出来。)
我已经从事三缝实验研究十多年了。2010年,我和我的同事在《科学》杂志上发表了我们的第一个结果。2014年,我和我的团队开始在印度卡纳塔克邦的Gauribidanur天文台使用微波进行新的三缝实验试验。我们在玉米地旁边的帐篷里的露天场地进行了这个项目。尽管对于精密物理实验来说,这个环境听起来可能很奇怪,但玉米为可能干扰我们测量的杂散微波提供了良好的吸收源。我们没有在空间中使用墙壁或大量可能反射波的设备也很有帮助。此外,我们偏远的位置手机信号很差——这是避免污染的另一个好处——而且我们能够大规模地进行实验。
我们的装置使用了两个喇叭天线——一个用于释放微波光子,另一个用于探测它们。它们之间是一个带有三个槽的板,每个槽宽10厘米,间距13厘米。为了忠实于第一个基于狭缝的实验风格,我们将探测器安装在导轨上,我们可以移动导轨以测量作为探测器位置函数的不同干涉图案。我们发现,我们测量的干涉图案与波动方程给出的近似解ΨA + ΨB不符,但它与包含非零索尔金参数的解相符。我们还使用了阻挡材料来阻挡狭缝之间的空间,基本上阻止了光子在狭缝之间传播并与相邻狭缝相互作用。当我们这样做时,我们看到索尔金参数的值随着阻挡块的大小而变化——这表明该参数确实测量了狭缝之间的相互作用,并且它根据相互作用的程度而变化。这一发现确立了我们测量的修正项不是我们未能理解的实验中的某些系统误差,而确实是我们正在寻找的东西。
我们的研究首次明确验证了索尔金参数作为经典微波域中叠加原理的修正项。这项结果于2018年6月发表在《新物理学杂志》上,已经导致了一些教科书的修订,并且影响了我们对基础物理学的基本理解。它们也可能对天文学和天体物理学中研究来自早期宇宙信号的工作产生影响。这项研究通常涉及散布在地面的无线电天线阵列。通常,不同天线接收到的数据会被加在一起。但是,既然我们知道波动方程的解不仅仅是各个解的总和,那么一些计算可能需要使用正确的索尔金参数进行更新。我们的发现最终可能有助于科学家为这些观测开发更好的误差模型。
图片来源:尼克·博克尔曼
量子三元比特
我们的实验不仅在理论上很有趣,而且在实践中也可能很有趣。我们希望使用我们的三缝工艺来帮助设计用于量子计算的新工具。
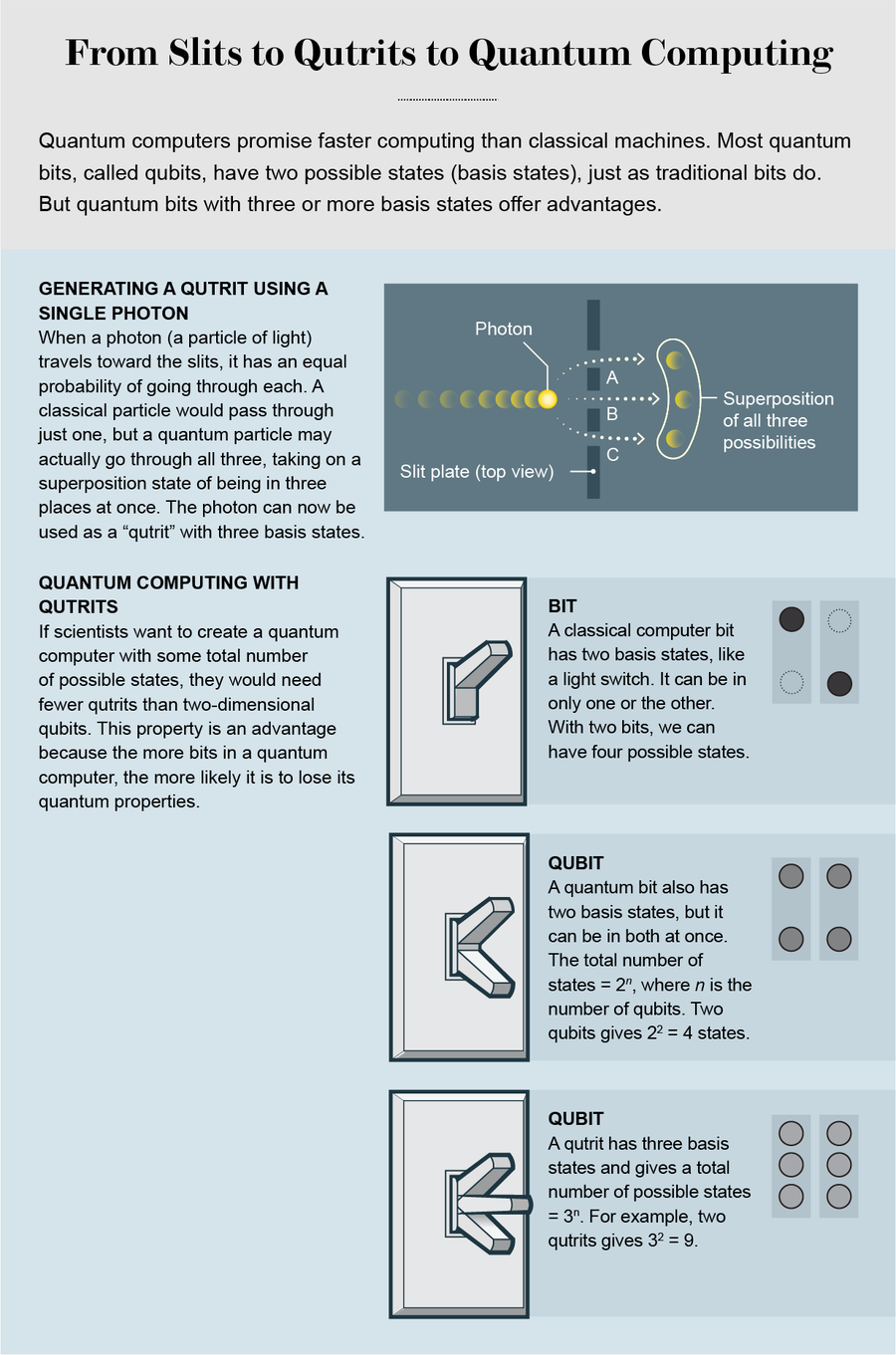
量子计算机利用叠加等量子定律,使计算速度比经典计算机快得多。将传统的计算机比特想象成一个电灯开关:它可以是“开”或“关”(分别对应于二进制代码中的值1或0)。然而,在量子世界中,开关不必是开或关——它可以两者都是。在量子比特中,我们定义了一种状态,该状态以有限的概率同时处于开状态和关状态。这两种状态的组合以及每种状态的概率是叠加的本质。
构成叠加态的两种状态称为基态。一个普通的量子比特有两个基态,对于n个量子比特,可以访问2n种可能的状态。因此,对于两个量子比特,有22 = 4种可能的状态。然而,对于n个经典比特,状态只发生在2n种可能性中的一种,而对于n个量子比特,所有2n种可能性都可以共存。量子计算的力量来自巧妙设计的量子算法,这些算法可以在执行期间利用叠加态,并以比经典计算机快指数级的速度执行某些类型的操作。
然而,为了实现这个目标,我们需要相当多的量子比特——当然不仅仅是两个。社区中许多人已经开始努力实现的一个数字是n = 50,这为量子算法提供了许多有趣的可能性。
有了50个量子比特,我们就有250种可能的状态可用于量子运算。最近,谷歌声称它通过在54量子比特量子处理器上成功实现随机抽样计算,实现了这个里程碑。然而,获得大量量子比特说起来容易做起来难。我们放在一起的量子比特越多,它们失去叠加的特殊量子能力并崩溃回正常的经典比特的可能性就越大。当量子比特与外部环境相互作用并失去“相干性”时,就会发生这种情况。当我们尝试将更多量子比特放入相干叠加态时,长时间维持这种状态变得越来越困难。这很像把人放到一个房间里参加聚会。如果你在一个100平方英尺的房间里有10个人,那么有足够的空间让他们共存而不会进入彼此的空间。如果我们将人数增加到30人,就会开始出现拥挤,这会导致普遍失去和平共处。量子比特也会发生同样的事情。
通常策略的一种替代方案是增加每个量子比特的维度,而不是试图在同一空间中容纳更多量子比特。为了了解为什么这会有所帮助,让我们回到一个基本的数学问题
23是多少?答案当然是 8 (2 × 2 × 2 = 8)。
现在,32是多少?这里的答案是 9 (3 × 3 = 9)。
这些结果是同一数量级的——非常接近。因此,如果我们使用两个三元量子比特(即三维量子比特)而不是三个量子比特,我们将可以访问相似数量的可能状态。因此,与其尝试增加指数,为什么不尝试改变底数呢?如果我们增加基态的数量,我们将需要更少的比特来实现相同的目标。这种认识定义了更高维度量子系统中的研究。
我们的策略还有另一个好处:我们不再受二进制代码的约束。考虑一场足球比赛的结果。通常我们认为有两种结果,“胜”和“负”,可以使用两种状态来指定,所以在量子世界中,一个量子比特就足够了。如果我们再添加两种可能的结果,例如“放弃”和“平局”,一个量子比特不足以声明结果。我们需要两个量子比特。但是,如果我们有一个四态系统,一个就足够了。这样的系统将是一个“四元量子比特”。
因此,更高维度的量子系统或量子数字系统可以在更少的系统中打包更多信息。从理论上讲,这种优势已被证明在量子计算机的某个目标方面具有优势——即使用所谓的量子密钥分发创建防黑客通信。在这种方法中,双方创建一个共享的秘密“密钥”,只有他们可以使用该密钥来解码消息。如果你可以通过增加基态的数量来增加量子比特的维度,那么结果就是一个更能抵抗某些类型攻击的密钥。除了密钥分发中更高的安全性的可能性之外,量子数字还承诺在真正的随机数生成中具有更大的随机性——这是量子计算机的另一个有希望的应用。
尽管有这些好处,但基于量子数字的系统也有一些缺点。实际上很难想出稳定的物理系统,其中所有基态都同样容易达到。例如,有时系统可能会偏向其最低能量或基态,并且由此产生的计算可能会带有这种偏差。第二个障碍仅仅是,这条研究路线比量子比特更新,因此为量子数字开发的算法和工具更少。尽管有很多事情要做,但未解决问题的数量使这项研究令人兴奋且潜力巨大。
迈向量子计算机
那么,我们如何从基本的三缝实验过渡到工作的三元量子比特系统?第一步是生成单光子。
我们从非常强的激光束开始,将其照射到特殊的晶体材料上。在某些条件下,大约每108到1010个光子中就有一个在称为下转换的过程中分裂成两个能量较低的光子。子光子总是成对出现。我们使用单光子探测器测量其中一个光子,并且由于我们知道它们是同时产生的,因此该测量预示着另一个光子的存在。然后我们可以使用第二个光子进行实验。
在我们团队的工作中,我们研究了“母”光子的特性,以确保子光子共享其特性。母光子 направляется 向三个狭缝,其空间轮廓 затем 模拟三缝轮廓。子光子反过来也携带这个轮廓。光子进入叠加态,这给了我们一个“空间箱”三元量子比特,其三个基态是三个狭缝位置。
尽管如此,我们创建的这个三元量子比特与功能性量子计算机所需的三元量子比特还相差甚远。我们需要使用我们的狭缝系统生成大量的三元量子比特,然后将它们馈送到具有所谓门操作的架构中,这些门操作能够使用三元量子比特来执行计算。这个领域是我团队当前工作的重点。我们必须设计完成这种操作所需的特定光学元件,然后将所有东西小型化,使其能够定义一个工作计算机系统。
因此,三缝代表了物理学研究的阴阳两面——既是基础的又是功能性的。我们对叠加原理及其首次测量的修正项的研究探索了物理学的最基本概念。与此同时,基于三缝的量子数字代表了在迈向更高维度量子计算和量子通信方面的技术壮举。事实证明,这个最著名的物理实验仍在提供新的见解和可能性。”

