2007年,亚历山大·沙波瓦洛夫为第六届国际柯尔莫哥洛夫数学竞赛提出了一个不寻常的硬币称重问题 [5]。
一位法官面前有 80 枚看起来相同的硬币,他知道其中有两枚或三枚假币。所有真币重量相同,所有假币重量也相同,但假币比真币轻。
一位律师知道恰好有三枚假币,并且知道是哪三枚。律师必须使用天平来说服法官,确实有三枚假币,并且不可能只有两枚假币。她受合同约束,不得泄露任何关于特定硬币的信息。她应该如何进行?
为什么这个问题如此不寻常?让我们回顾一下历史。第一个硬币称重问题出现在 1945 年左右 [6, 7]。在所有这些问题中,目标仅仅是在许多真币中找到一枚假币。在那之后,出现了许多推广:新版本的假币问题包括找到多枚假币,区分任意重量的硬币等等。然而,所有这些问题的附加目标都是尽量减少定位假币所需的称重次数 [2]。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
沙波瓦洛夫的难题是第一个将注意力从消除硬币隐私转移到维护硬币隐私的问题。这个难题非常重要且具有现代意义;像许多其他“硬币称重”问题一样,它不是关于硬币,而是使用硬币来模拟想法,并创建真实生活中的隐私问题及其潜在解决方案的简化版本。
简化版本
让我们考虑一个更简单的沙波瓦洛夫难题版本,以便入门
示例 1。 在与之前类似的情况下,律师想向法官证明假币的数量正好是两枚,而不是一枚。
策略 1。 律师将硬币分成两堆,每堆 40 枚,以便每堆正好包含一枚假币。然后,她将这两堆硬币放在天平的不同托盘中。
天平平衡,这意味着两个托盘中假币的数量相同。因此,假币的总数是偶数,在本例中,正好是 2 枚。对于任何特定的硬币,法官都无法明确地说出它是真币还是假币;因此,我们成功地完成了任务。
在继续之前,让我们介绍一些符号。我们将用 t 表示硬币总数,用 ƒ 表示假币的实际数量,用 d 表示我们试图证伪的假币数量。
我们还想为一种策略或一系列称重命名,在这些称重之后,法官对任何特定硬币的真伪一无所知。Knop [4] 建议将此类策略称为“沙波瓦洛夫策略”,以纪念该难题的设计者。其中一位作者 [3] 使用了“不泄露”这个名称。我们不喜欢“不泄露”这个名称,因为我们计划表明所有策略都会泄露一些信息。我们喜欢“沙波瓦洛夫”这个名称,但我们也希望有一个描述性的名称。
定义 1。 我们将一组称重或一种策略称为“谨慎”策略,在这种策略中,不会泄露关于任何特定硬币的信息。否则,我们将这组称重称为“不谨慎”策略。
目前,我们只关心谨慎(沙波瓦洛夫)策略。如果 ƒ 和 t 有一个公约数 m ,但 m 不能整除 d,则可以推广策略 1
策略 1*。 律师将硬币分成 m 个相等的组,每组包含 ƒ/m 枚假币,并证明所有组的重量都相等。
现在我们可以回到最初的难题并讨论其解决方案。
原始问题的解决方案
受到前一个示例中使用的策略的启发,律师可以尝试将 80 枚硬币分成三组,每组包含一枚假币。显然,80 不能被 3 整除,所以她将硬币分成三个尽可能大的相同大小的组:每组 26 枚,每组一枚假币。律师使用天平进行两次称重,向法官证明所有三组 26 枚硬币的重量都相同。法官可以得出什么结论?他可以得出结论,要么有 3 枚假币——每组一枚,要么有 2 枚假币,并且它们在剩下的 2 枚硬币组中。不幸的是,这种策略不足以向法官证明正好有 3 枚假币。律师决定不放弃,并以下列方式调整策略
策略 2。 律师首先证明包含一枚假币的 26 枚硬币的三组重量相同。她继续将剩余组中的一枚硬币与不在剩余组中的一枚真币进行比较。
该策略证明假币的数量必须是 3 枚,而不是 2 枚。然而,这种策略是不谨慎的——我们将其留给读者来验证这两个断言。总的来说,想出这个问题的解决方案已被证明非常棘手。大多数提出的策略都包含一些细微的缺陷,要么未能排除 2 枚假币的可能性,要么至少泄露了一枚硬币的身份。
现在我们将介绍来自竞赛的官方(谨慎)解决方案,并再次请读者对其进行分析。
策略 3。 律师将所有硬币分成 5 堆:A 和 B 各有 10 枚硬币,C、D 和 E 各有 20 枚硬币,以便三枚假币分别在 A、D 和 E 堆中。然后,律师进行三次称重。第一次称重,她将 A + C 与 B + D 进行比较,天平平衡。第二次称重,她将 A + B 与 E 进行比较,天平再次平衡。最后一次称重,她将 C + D 与 A + B + E 进行比较,并表明第二个托盘更轻。
现在我们为这个问题提供另一种谨慎策略。
策略 4。 律师将所有硬币分成九堆:A1、B1、C1、A2、B2、C2、A3、B3 和 C3,大小分别为 24、1、2、24、1、2、23、2 和 1。律师证明 A1 + B1、A2 + B2 和 A3 + B3 在天平上相互平衡。此外,她还表明 B1 + C1、B2 + C2 和 B3 + C3 的重量相同。
再一次,我们将其留给读者来证明假币有三种不同的分布方式
每组 A1、A2、A3 (大小分别为 24、24、23) 中各有一枚假币
每组 B1、B2、B3 (大小分别为 1、1、2) 中各有一枚假币
每组 C1、C2、C3 (大小分别为 2、2、1) 中各有一枚假币。
在每种情况下,我们都排除了存在两枚假币的可能性,并且没有泄露任何特定硬币的身份。
在 Knop 的文章 4 (俄语)中查看更多不足和正确的解决方案示例。
谨慎的硬币称重
最初的难题很棘手,但我们已经设法演示了两种解决方案。是否总是可以找到尊重每枚硬币隐私的解决方案?或者,在我们新的定义中,是否总是可以找到一组谨慎的称重?
让我们指出一个微不足道的事实,即如果 ƒ = 0 或 ƒ = t (因此律师必须向法官证明所有硬币都是真币/假币),那么每枚硬币的隐私都必然会因所证明的陈述而被侵犯。
为了防止泄露任何给定硬币的身份,我们将只考虑 0 < ƒ < t 的情况,因此我们试图证明的陈述本身就是谨慎的。然而,正如以下引理所证明的那样,在这种情况下,并非总是可以得到一组谨慎的称重。
引理 1。对于 t > 1 且 ƒ = 1 ,不可能有谨慎策略。
证明。 假设存在这样一种策略,并且律师说服法官假币的总数为 1 枚。现在考虑任何一次称重。如果天平平衡,那么两个托盘上的硬币必然都是真币。如果天平不平衡,那么我们知道较重托盘上只有真币。在任何一种情况下,一些硬币都被证明是真的,因此该策略是不谨慎的。
我们将其留给读者来证明,对于以下参数,也不可能得到谨慎策略。
• t > 1 且 ƒ = t − 1
• ƒ = 2 且 d = 0。
揭示因子和系数
考虑策略 1,即简化的案例,其中律师将硬币分成两组,每组 40 枚。假设法官知道有 2 枚假币。在称重之前,他猜对一枚假币位置的几率是多少?仅仅是 80 分之 2。称重后,法官知道每组 40 枚硬币中都有一枚假币,因此他找到一枚硬币的几率是 40 分之 1——与之前相同。
尽管看起来好像没有泄露任何信息,但事实恰恰相反。在称重之前,这两枚假币可以是 80 枚硬币中的任何一枚,这些假币的等可能分布的数量为 (802) = 3160。称重后,每堆 40 枚硬币中都有一枚假币,可能性数量减少到 (401)2 = 1600。在 [1] 中讨论了在成功策略之后尝试猜测单枚假币位置的一般挑战。
我们想引入揭示因子和揭示系数的概念来量化这种观察结果。在称重之前,如果法官知道假币的数量正好是 ƒ 枚,那么任何 ƒ 枚硬币的集合都可能是假币的集合。等可能性的数量为 (tƒ),我们称此值为“旧可能性”。称重后,可能性集合减少,因此并非任何任意 ƒ 枚硬币组都可能是假币的集合。我们将在称重完成后可能成为假币的 ƒ 枚硬币集合的数量称为“新可能性”。
定义 2。 我们将成功策略之后旧可能性数量与新可能性数量的比率称为揭示因子。我们将其表示为 X
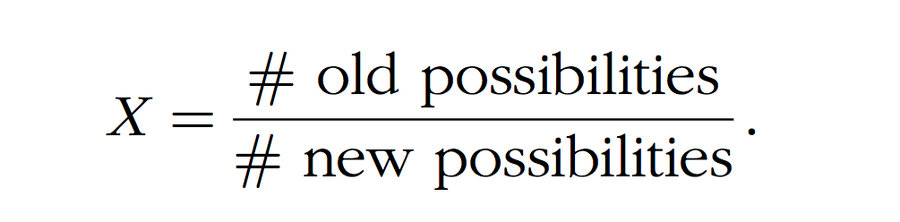
我们还想引入 [3] 中使用的“揭示系数”的概念。揭示系数是在证明正好有 ƒ 枚假币的过程中泄露的信息部分
定义 3。 揭示系数,用 R 表示,定义为 1 − 1/X
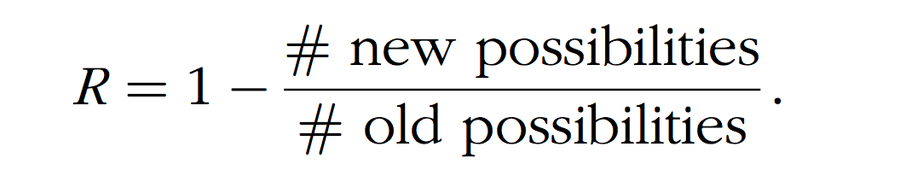
一种几乎不泄露假币确切位置信息的策略对应于更高数量的新可能性。由此可见,我们希望揭示系数和揭示因子都尽可能小,以最大限度地减少信息传递。
在策略 1 中,揭示因子 X 为 3160/1600 = 1:98。揭示系数 R 为 ( 3160 − 1600 ) / 3160 ≈ 0:494,略小于一半。策略 3 和策略 4 的揭示因子的计算更加复杂,留给读者完成。答案分别约为 10.27 和 6.20。
不同的策略泄露不同数量的信息
假设我们有 80 枚硬币,我们想证明有 4 枚假币而不是 3 枚;即,t = 80,ƒ = 4,d = 3。我们可以使用策略 1* 来进行:将所有硬币分成四堆,每堆 20 枚,每堆包含一枚假币。证明所有堆的重量相同告诉法官假币的数量必须是 4 的倍数,我们就完成了。但是,我们可以产生另一种谨慎策略:将硬币分成两堆,每堆 40 枚,每堆放入两枚假币。在比较这两堆硬币后,法官知道假币的数量是偶数。这两种策略都是谨慎的,但揭示因子和系数是不同的,我们将其留给读者检查。
第二种策略的揭示性明显较低;在这种情况下,将所有硬币分成更少的等效堆显然更可取。
揭示因子/系数可以为谨慎策略和不谨慎策略定义。令人惊讶的是,我们经常看到不谨慎策略比谨慎策略泄露的信息更少。让我们回到最初的问题及其“错误”的,或者说是不谨慎的解决方案,策略 2 中描述的解决方案。在称重后,法官知道 3 枚真币的位置。其他硬币分为 3 组,分别为 26、26 和 25 枚硬币,每组包含一枚假币。我们将其留给读者来检查揭示因子 X ≈ 4:86。尽管此策略是不谨慎的,并且 3 枚真币的隐私受到侵犯,但它比谨慎策略 3 和策略 4 的揭示性更低,后两者的揭示因子分别为 10.27 和 6.20。在某种程度上,被暴露为真币的三枚硬币有效地“牺牲”了它们的隐私,以使其他希望保持隐藏的硬币更加安全。
最优性证明
在这里,我们想展示某些参数的谨慎策略的最优性证明。即,我们考虑 t = 2k、ƒ = 2 和 d = 1 的情况,其中 k 是某个正整数 k > 1。我们已经讨论过使用一次称重的策略(参见策略 1*):将所有硬币分成大小为 k 的两堆,将假币放入单独的堆中,并比较这两堆硬币。
似乎很明显,这是“最不泄露”或最优的策略,但我们仍然需要证明。首先,我们引入更多定义和符号。在任何称重过程中,硬币出现在左托盘上用 L 表示,硬币出现在右托盘上用 R 表示,未参与的硬币(留在称重之外的硬币)用 O 表示。
在所有称重之后,每枚硬币的路径都可以描述为 L、R 和 O 的字符串。
定义 4。与每次称重中给定硬币的位置相对应的 L、R 和 O 字符串称为硬币的“路径”。
给定路径 ∂,我们将具有此路径的所有硬币的集合表示为 ∂,并将此集合的大小表示为 ∣∂∣。我们将介绍路径上的对合运算,称为共轭
定义 5。 给定路径 ∂,“共轭路径”,用 −∂ 表示,是唯一的路径,其中所有 R 都替换为 L,所有 L 都替换为 R。
请注意,这是一个对合运算,因为 =∂ = ∂。此外,唯一的自共轭路径是 O 的字符串。在称重之后,我们可以根据路径将所有硬币分成组。
在以下初步引理中,t 不必是偶数。
引理 2。如果 ƒ = 2 且 d = 1 ,则谨慎策略的路径集合具有以下性质:如果存在具有路径 ∂ 的硬币,则存在具有路径 −∂ 的硬币。此外,没有具有自共轭路径的硬币。此外,所有称重都是平衡的。
证明。 所有称重都必须是平衡的,否则较重托盘必须仅包含真币,并且该策略是不谨慎的。由此可见,两枚假币在任何时候都不能在同一个托盘中。此外,如果一枚假币在称重期间在一个托盘中,则另一枚假币必须在另一个托盘中以使其平衡。这意味着假币具有共轭路径。
由于上述条件,如果存在具有路径 ∂ 的硬币,并且没有具有路径 −∂ 的硬币,则 ∂ 中的所有硬币必然都是真币。
如果一枚硬币未参与任何测量,并且所有称重都是平衡的,那么我们尚未证伪只有一枚假币的可能性。因此,不能有任何具有自共轭路径的硬币。
现在我们准备证明偶数枚硬币的最优性定理。
定理 3。 如果 t 为偶数,ƒ = 2 且 d = 1 ,则策略 1 是任何可能策略中最不泄露的策略。
证明。 所有硬币都根据相同的路径被划分为组,并且所有路径都通过共轭进行配对。路径集合为 ( ∂j∂j) = 1, 2, 3....如果一枚假币属于 ∂j,则另一枚假币必须属于 ∂j。这意味着新可能性的总数为
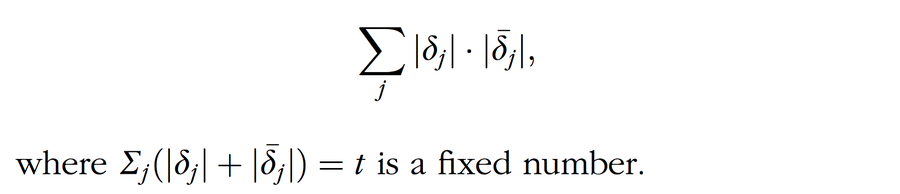
标准代数论证表明,当恰好存在一个路径对,其中两个路径的大小相等时,新可能性的数量最大化。
一个奇特的案例:奇数 t 的情况
我们想讨论更复杂情况下的最优性:当硬币总数为奇数、ƒ = 2 且 d = 1 时。以下引理的证明可以在 [1] 中找到。
引理 4。对于给定参数的谨慎策略必须生成至少 6 个不同的路径。在这些路径中,将至少有 3 个共轭对;此外,每对中两组硬币的数量必须具有不同的奇偶性。
现在我们将提供更多谨慎策略不存在的示例,再次将证明外包给 [1]。
推论 5。对于 ƒ = 2 且 d = 1,当 t = 3、t = 5 或 t = 7 时,不可能有谨慎策略。
当 t > 7 时会发生什么?通过修改策略 4,我们可以创建一个适用于奇数 t > 7 的谨慎策略。
策略 4*。 考虑大小分别为 ⌊ t / 2 ⌋ − 2 和 ⌊ t / 2 ⌋ − 3 的堆 A 和 Ā。堆 B 和 B 的大小分别为 1 和 2。堆 C 和 C 的大小分别为 2 和 1。律师将两枚假币分配到堆 A 和 A、B 和 B 或 C 和 C 中。
此策略进行两次称重。在第一次称重中,律师将属于 A 和 B 的 ⌊ t / 2 ⌋ − 1 枚硬币与属于 A 和 B 的 ⌊ t / 2 ⌋ − 1 枚硬币进行比较。在第二次称重中,她将属于 B 和 C 的三枚硬币与 B 和 C 中相同数量的硬币进行比较。
引理 6。对于 ƒ = 2 且 d = 1,当 t 为奇数且 t > 7 时,策略 4* 是谨慎的。
证明。 所有硬币都在天平上,并且所有称重都是平衡的。这意味着必然有两枚假币。
由于假币可以属于具有共轭路径的任何一对组,因此没有泄露任何关于特定硬币的信息。
引理 7。如果 t 为奇数,ƒ = 2 且 d = 1 ,则策略 4* 是最不泄露的策略。
该证明与定理 3 的证明类似,可以在 [1] 中找到。
结论
假币真的需要在法庭上获得律师的保护吗?很可能不需要。但是数学家以将难题简化为更简单、更易于管理的问题为生。简而言之,我们的讨论表明,从数据库收集聚合信息会在过程中泄露一些额外的信息;本文是我们尝试量化泄露多少信息的尝试。
参考文献
[1] N. Diaco, T. Khovanova, Weighing Coins and Keeping Secrets, arXiv:1508.05052, (2015).↩
[2] R. K. Guy and R. J. Nowakowski, Coin-weighing problems, Amer. Math. Monthly, 102 (1995), 164–167.↩
[3] T. Khovanova, Unrevealing Coin Weighings, available at http:// blog.tanyakhovanova.com/2009/08/unrevealing-coin-weighings/.↩
[4] K. Knop, The mystery of fake coins, Matematika, N8 (2008), 29–31 (in Russian).↩
[5] Kolmogorov Math Tournaments, http://cdoosh.ru/kolm/kolm.html.↩
[6] E. V. Newbery, The penny problem, Note 2342, Math. Gaz., 37 (1953) 130.↩
[7] B. L. Schwartz, Letter: Truth about false coins, Math. Mag., 51 (1978) 254.↩
[8] Y. Zhang, Coins and Low-Knowledge Proofs, Concrete Nonsense blog, available at https://concretenonsense.wordpress.com/2009/ 12/17/m-3-coins-and-low-knowledge-proofs/.↩
