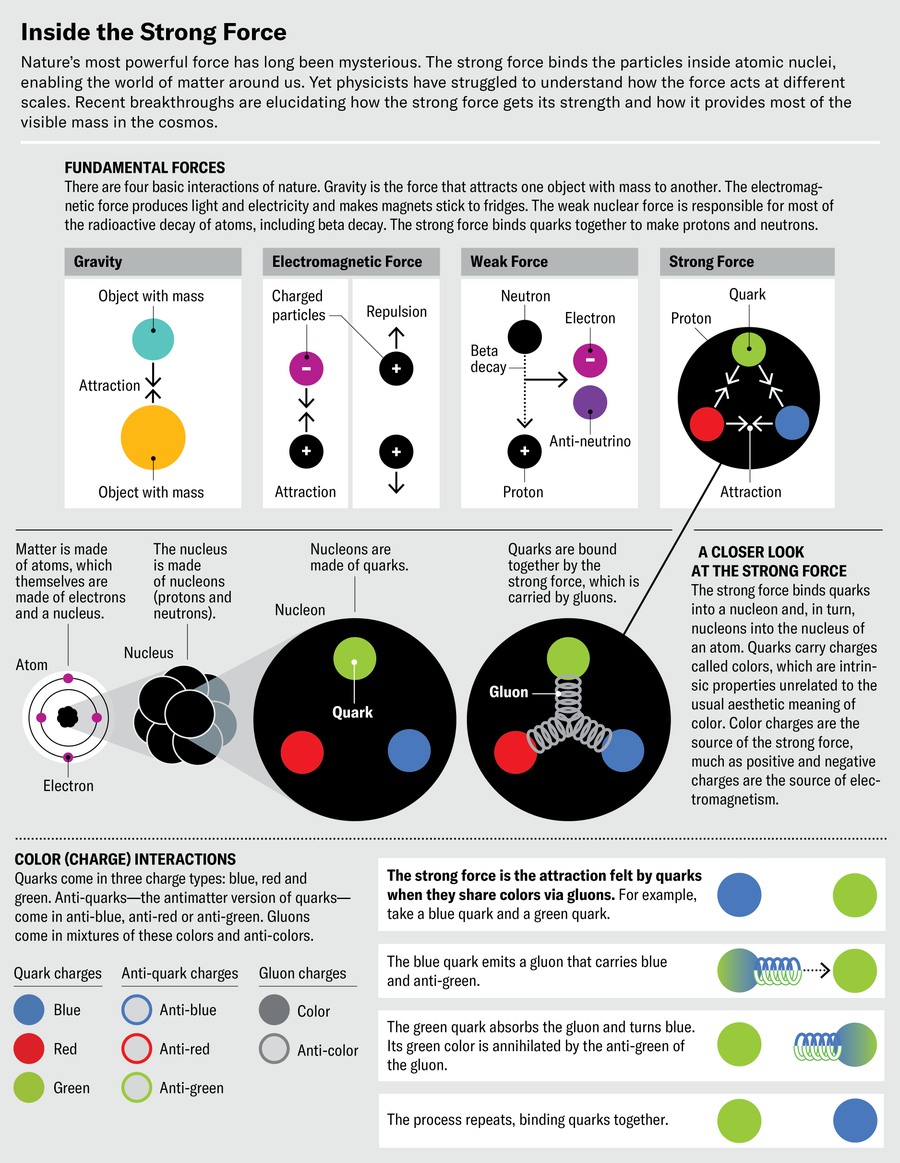
宇宙中最强的力被称为强力,这很贴切。我们永远无法亲眼目睹它可怕的力量,因为它只在亚原子距离范围内起作用,在那里它将夸克束缚在质子和中子内部,并将这些核子结合成原子核。在自然的四种基本力中,强力无疑是最强大的——它比引力强 100 万万万万万万万万万万万万万万万万万万万万万万万万万万万万万万万倍。它也是最神秘的。
尽管大致了解强力与其他力相比如何,但科学家们并不确切知道强力有多强。其他三种力——引力、电磁力和弱核力(负责某些放射性)——的测量要好得多。例如,电磁力的强度,用其“耦合常数”表示,其测量精度与纽约和洛杉矶之间的距离相同,误差在几根头发的宽度之内。然而,强力的耦合常数,称为 αs(“阿尔法 s”),是这些量中最不为人所知的。对 αs 的最佳测量精度比电磁测量的精度差 1 亿倍。
即使是这种程度的(不)确定性也仅在强力理论的最简单领域中已知,即仅在自然界中一些最稀有和最极端事件中涉及的极高能量下。在与我们周围世界相关的较低能量下,强力通过变得真正强烈而名副其实,并且关于该范围内 αs 的具体信息很少。直到最近,还没有人对这个尺度的 αs 进行任何实验测量。对其值的理论预测毫无帮助,涵盖了从零到无穷大的整个范围。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。
珍·克里斯蒂安森
强力的强大使得在很多方面都难以研究它。描述其工作原理的理论,称为量子色动力学,非常复杂,我们无法使用它来进行直接计算或精确预测。这种复杂性的原因之一是强力的载体——一种称为胶子的粒子——与自身相互作用。相比之下,电磁学很简单,因为它的载体光子是不带电荷的。但胶子携带强力的电荷版本,称为色荷,其自相互作用很快就会失控。因此,尽管强力对核物理和构建物质世界非常重要,但研究人员并非完全喜爱它。相反,许多人将强力真正强大的领域视为“禁地”(Terra Damnata),一个不惜一切代价也要避免的领域。
然而,理解强力对于解释我们周围物质的复杂性至关重要。事实上,强力占可见宇宙中约 99% 质量的来源。(剩下的 1% 来自希格斯玻色子。)而现在,经过半个世纪的努力,科学家们终于开始揭示强力的一些秘密。我们中的一位(德厄尔)最近首次测量了 αs 在禁地内如何变化,我们中的两位(布罗德斯基和罗伯茨)独立开发了新的理论预测来解释这些数据。禁地看起来比以往任何时候都更受欢迎。现在我们可以探索这片领域,我们有望学到更多。我们终于有能力从第一原理分析计算量子色动力学的各个方面。此外,探索强力的这个范围可能有助于我们理解宇宙的拟议统一理论,以及空间和时间中存在多少维度的问题。

磁铁引导粒子通过托马斯·杰斐逊国家加速器实验室 (Jefferson Lab) 的连续电子束加速器设施 (CEBAF)。
图片由杰斐逊实验室提供
如果 αs 是一个常数,它怎么会变化呢?答案与量子环的概念有关,也称为真空极化。量子理论揭示,空间的“真空”实际上充满了微小的粒子,这些粒子不断出现和消失在波动的云中。与这些虚粒子的相互作用会导致力偏离其经典行为,因为所谓的量子环。当这个概念首次被引入时,量子环是一个令人不快的意外,因为它们预测了无限量——这是一个明显的迹象,表明有问题。但最终,物理学家们弄清楚了如何驯服这些无限性,并将量子环的所有修正都吸收到描述力载体的方程中。因此,在量子色动力学 (QCD) 中,量子环修正影响胶子的行为,并决定 αs 随夸克之间距离的变化量。由于量子环的这种新的距离依赖性存在于耦合常数中,这些量失去了它们的常数性。因此,我们从现在开始将其称为“耦合”。
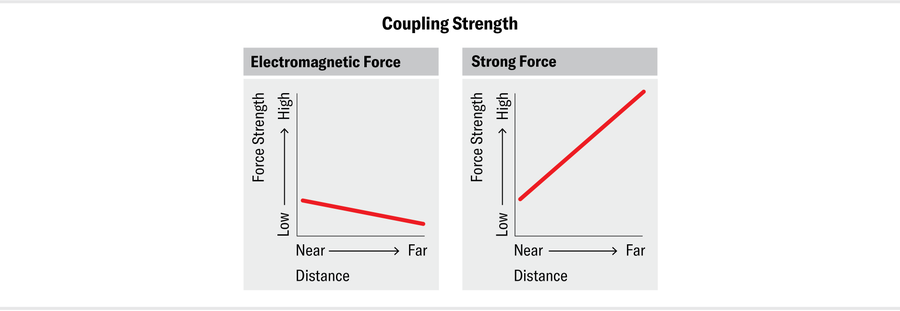
对于大多数力,耦合随距离变化缓慢。例如,从人类探测到的最小尺度到日常尺度,电磁耦合 αem 仅下降其值的约 10%。然而,对于强耦合 αs,变化是巨大的:即使在物理学家可以舒适地计算 αs 的领域内(即,远离禁地),其值也变化了几个数量级。另一个更重要的区别是,电磁耦合随着距离的增加而减小。然而,对于强力,αs 随着距离的增加而增加。如果您试图将质子内的两个夸克彼此拉开,它们之间的吸引力就会变得更强。事实上,它增长得如此强大,以至于几乎不可能将夸克从彼此剥离开来——强力将它们“禁闭”起来,您永远找不到单个的夸克。同样的规则适用于夸克和胶子之间以及胶子和胶子之间的相互作用。另一方面,这些相互作用在短距离内很弱:您越靠近夸克,它的束缚就越松散。αs 在短距离处的小值被称为渐近自由,其在 20 世纪 70 年代的发现最终为其先驱赢得了 2004 年诺贝尔物理学奖。
珍·克里斯蒂安森
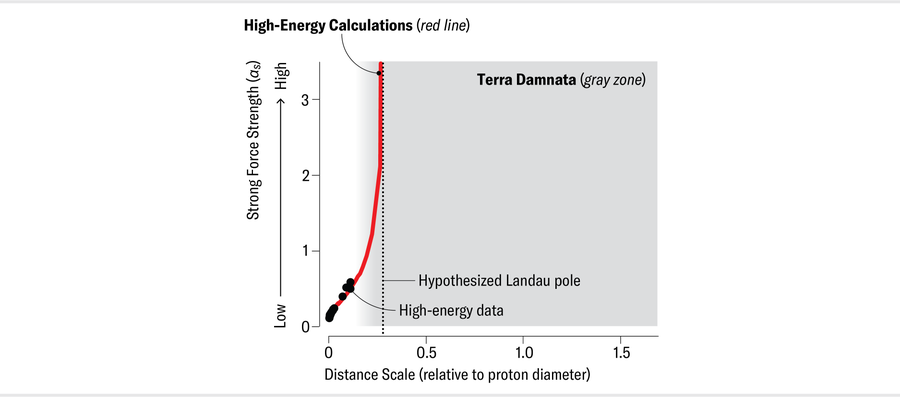
在短距离处,αs 很小,物理学家可以使用与我们用于电磁力和弱力相同的方法进行计算。但这些方法不适用于较长距离的 QCD——例如,质子的大小。按照日常标准,这个长度仍然非常小(质子的大小是原子的五万分之一,半径约为十亿分之一米的百万分之一)。然而,它代表了粒子物理学中的一个广阔领域。问题在于 αs 增长得太快。在我们能够达到费米之前,αs 变得太大,标准计算方法无法适用。这就是为什么(甚至不是很)长距离领域变成了禁地。
珍·克里斯蒂安森
由于通常的计算方法不可用,物理学家尝试了其他策略,但它们要么未经充分测试,要么不精确,并预测 αs 的长距离极限可能介于零和无穷大之间。通常的短距离计算方法预测 αs 在长距离范围内的值为无穷大。但是,这种无穷大,在物理学家列夫·朗道之后被称为朗道极点,仅表明计算方法失败,而不是告诉我们关于强力的信息。确定 αs 在距离处的作用至关重要。
许多物理学家广泛努力的突破终于出现了。这个故事分三个阶段展开,我们中的一位参与了每个阶段。
第一步是幸运的。在 20 世纪 90 年代后期,德厄尔是弗吉尼亚州托马斯·杰斐逊国家加速器实验室(杰斐逊实验室)的一名博士生,该实验室拥有一台粒子加速器。他的测量跨越了短距离和禁地之间的过渡。当时,他知道朗道极点,但不知道它是假的。他感到困惑的是,在 αs 应该明显变化的距离处(或者他认为应该如此),似乎什么都没有发生。数据完全平滑,没有他被引导期望的爆发迹象。这些测量结果似乎并没有困扰更有经验的科学家,他们已经习惯于在这个区域收集数据,而且学生在用尽欢迎之前只能提出这么多幼稚的问题。因此,他将这个问题添加到他不了解世界的长长清单中,以便(可能)以后回答,然后继续前进。
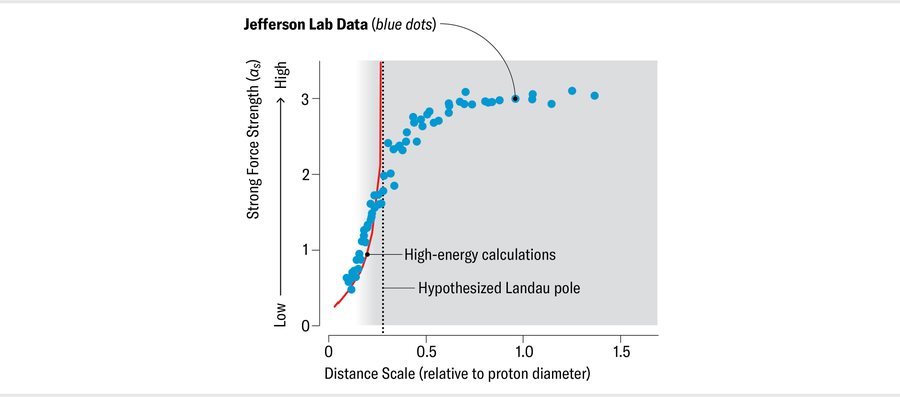
珍·克里斯蒂安森
几年后,他使用他的数据和杰斐逊实验室的其他测量结果来测量一个称为比约肯积分的量,该积分以詹姆斯·比约肯的名字命名,他是强力研究的先驱之一。比约肯积分与质子和中子内部夸克自旋的方向有关,并且作为奖励,只要您远离禁地,它也提供了一种相对容易的方法来计算 αs。因此,德厄尔能够在短距离的可靠领域测量 αs。出于好奇心和喜欢实验的倾向,他还检查了该公式对长距离的预测。这个实验只是为了好玩,他非常清楚他不应该认真对待答案。但他的分析表明,αs 远非随着距离的增加而急剧变化,而是停止增长并变为常数。
德厄尔与他的博士生导师,杰斐逊实验室的工作人员科学家陈建平分享了这个令人震惊的发现,陈建平评论说,这个 αs 看起来像他以前见过的预测。德厄尔深入研究过去的研究,发现了其他耦合计算在长距离处变为常数的例子,很像他在数据中看到的情况。也许他有趣的 αs 计算毕竟揭示了强力的真实行为?这是一个幸运的巧合,因为尽管没有人意识到这一点,但比约肯积分非常适合计算长距离处的 αs。虽然大多数测量探测了许多夸克之间的相互作用(因为夸克永远不会单独存在),但比约肯积分设法过滤掉大多数多夸克过程,并将对单个夸克的影响分离出来。事实证明,这种 αs 的计算几乎不适用于任何其他类型的核子数据。
由于德厄尔的 αs 可能有意义,他想知道他是否可以在物理学会议上展示它,而不会有太大的被嘲笑的风险。不过,他很担心,因为他的测量结果似乎与强力强度会持续增长的普遍智慧相矛盾。但他决定冒险。碰巧的是,布罗德斯基参加了其中一次会议,并帮助德厄尔为这项工作奠定了更坚实的理论基础。这次会议是富有成果的合作的开始,一直持续到今天。
当德厄尔通过实验探索 αs 时,布罗德斯基正在与盖伊·德·特拉蒙德·佩拉尔塔和汉斯·冈特·多施合作,开发一种新的方法来计算长距离处的 QCD 性质。他们的策略使用了一种称为全息术(通常用于研究黑洞和引力)的数学工具,通过使用在五维空间中完成的引力计算结果来推断强力在我们四维时空(三个空间维度加上一个时间维度)中具有较大 αs 值时的行为。(这种方法所依据的额外维度是代表实际物理,还是仅仅是简化问题的数学工具,就像经典物理学中使用虚数一样,没有人知道。)这种研究强力物理学的新颖方法,即所谓的轻锥全息术,可以确定长距离处的 αs,并预测将夸克和胶子限制在核子内的相互作用。
布罗德斯基长期以来一直熟悉 αs,并且知道寻找电磁力、弱力和强力统一理论的尝试似乎要求 αs 在长距离范围内变为有限值。事实上,他预计会出现这样的结果,因为夸克被限制在核子内,这意味着夸克和胶子量子环不能大于质子的大小。没有更多的环意味着耦合不再演化。因此,尽管德厄尔对 αs 的测量结果并没有让他感到惊讶,但他很高兴看到实际上有可能测量长距离处的 αs,并且结果表明它是恒定的。
布罗德斯基和德·特拉蒙德·佩拉尔塔联系了德厄尔,讨论如何使用他们的轻锥全息术方法计算 αs 并继续计算。2010 年发布的结果令人欣慰:他们的 αs 与德厄尔的实验数据完美匹配。这尤其引人注目,因为该计算没有任何可调参数。他们既没有摆弄设置,也没有乱用“凑合”因子。
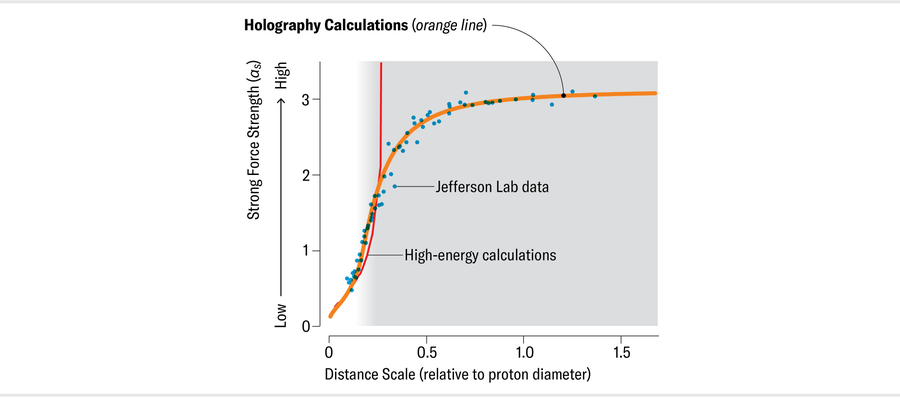
珍·克里斯蒂安森
当然,全息术是一种令人兴奋的新颖方法,用于研究量子色动力学(和量子引力),但它与使用 QCD 本身不同。但我们知道,它至少很好地模拟了 QCD,这表明未来的物理学家可能能够证明引力和强力行为之间存在某种等效性。尽管如此,为了放心地说我们真正计算了长距离处的 αs,我们需要基于 QCD 的计算。一种自然的方法是求解该理论的运动方程,QCD 中的运动方程描述了所有强力量如何随时空变化而演化。
德厄尔在 2005 年发表了他的第一个关于 αs 的结果,几乎是 20 年前。当时,罗伯茨对它们感到困惑,问自己,这种耦合测量,似乎专门与单个 QCD 过程相关联,可能与该理论的运动方程有什么关系。这样的方程需要一个对所有过程都相同的通用耦合。他将这个问题放在一边,然后继续前进。
九年后,在 2014 年他与同事在意大利特伦托的欧洲核物理理论研究中心及相关领域组织的会议期间,他重新审视了德厄尔的 αs。到目前为止,理论家们已经采用了两种平行的策略来使用 QCD 的运动方程来理解强力理论。“自上而下”的方法试图通过胶子的性质来预测 αs。“自下而上”的方法旨在通过将预测与实验数据进行比较,使用可直接测量的量来推断 αs。
在 2014 年的会议上,一位杰出的同事指出,这两种方法得出了截然不同的结果,无法调和。然而,这位同事并不知道罗伯茨与他的合作者雷·张在自下而上的方法方面取得的最新进展。在挑战的刺激下,两人在 24 小时内就获得了自下而上耦合估计的结果。他们与也在会议上的自上而下领域的两位主要参与者丹尼尔·比诺西和约阿尼斯·帕帕瓦西里乌分享了这些结果,该小组共同确定自上而下和自下而上的 αs 结果是相互兼容的。平行的流合并了。
现在我们面临一个关键问题:我们如何将德厄尔的耦合测量结果与我们使用 QCD 运动方程计算的值联系起来?如果我们能够做到这一点,那么我们将弥合最后的差距。
罗伯茨的下一步是与物理学家何塞·罗德里格斯-金特罗交谈,他长期以来一直致力于自上而下的方法,并且可以访问 QCD 计算机模拟的结果。在与比诺西、帕帕瓦西里乌和一位新团队成员塞德里克·梅兹拉格进行了一些来回的头脑风暴后,该小组得出了一个通用 QCD 耦合。令人惊讶的是,这个结果实际上与德厄尔的数据以及布罗德斯基及其同事的全息术计算无法区分。此外,与全息术结果一样,新的预测是无参数的:没有微调或修改。这一事实意味着该协议意义重大。
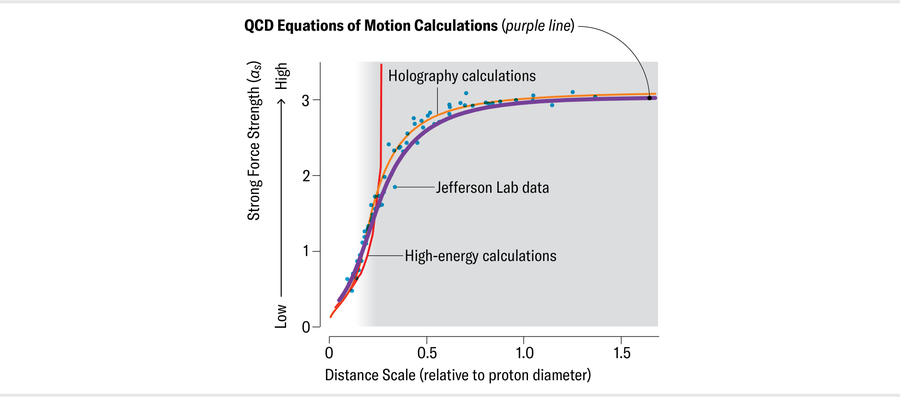
珍·克里斯蒂安森
自那时以来,利用来自自上而下、自下而上和模拟方法的改进信息,该小组更新了其理论分析。科学家们发现,在禁地之外,他们的耦合和德厄尔的数据的吻合度优于 1%。此外,进入禁地后,他们发现夸克之间复杂的相互作用可能会破坏这些耦合之间的联系,但由于比约肯积分基础过程的物理特征,这些相互作用在很大程度上会相互抵消。这是德厄尔的幸运之处:他偶然选择了一个过程,其耦合与从 QCD 运动方程导出的通用结果最密切相关。
现在,我们首次拥有了涵盖整个长度尺度范围(包括以前无法到达的禁地)的令人信服的 αs 数据和计算。关键发现是,随着距离的增加,耦合停止增长,而不变的常数再次变得恒定。这一发现具有深远的意义。

CEBAF 大接收度谱仪进行了一些测量,这些测量有助于定义前所未有的尺度下的强力。
图片由杰斐逊实验室提供
首先,了解所有距离处的 αs 在实践中非常重要:物理学家现在可以解析预测以前无法获得的许多量。自然界中与强力有关的大多数现象,从我们体内原子的最深层结构到中子星的内部运作,都由 αs 的强度决定。由于这种耦合主要由其长距离行为决定,而我们现在知道它是有限的而不是无限的,因此我们开辟了一个可能的计算新世界。
在更深层次上,QCD 运动方程的解有助于揭示宇宙中 99% 可见质量的起源。这种质量来自原子,而原子的大部分质量都在其质子和中子中(电子相对较轻)。但是质子和中子的质量从何而来呢?构成它们的夸克本身也几乎没有质量。但在质子的尺度上,我们关于 αs 的启示表明,夸克在其周围聚集了胶子云,从而产生了质子的大部分质量。本质上,强力施加的强大结合能将夸克束缚在一起,几乎贡献了所有的质量(记住,阿尔伯特·爱因斯坦揭示能量和质量是同一枚硬币的两面)。因此,如果您的体重为 160 磅,那么其中超过 158 磅来自量子色动力学,特别是由于将 αs 冻结为常数的机制。希格斯玻色子只贡献了很小的剩余部分——夸克和电子自身拥有的微小质量。
更重要的是,长距离处 αs 的静态性质意味着 QCD 是第一个只预测有限量的完整量子场论。所有其他已知的量子场论,包括描述电磁力的量子电动力学,在非常高的能量下都会遇到无限的朗道极点。因此,QCD 可能会引领解释许多超出我们当前理解范围的现象。
沿着这条推理路线继续下去,我们可能会了解到,例如,具有 10 个、11 个或 26 个时空维度的弦理论是否对于理解我们的宇宙是必要的,或者相反,对我们牢固建立的四个时空维度的清晰理解是否足以胜任。目前核物理学家和粒子物理学家之间的兴奋是显而易见的。