通常,每条地铁线路在地图上都有自己的颜色。 显而易见的原因是,这些颜色应该尽可能地不同。 假设要修建一条新的地铁线路。 现在,我们将解释一种为新线路选择一种或多种颜色的策略,使其与旧线路以及彼此之间尽可能不同。 这通过使用莫斯科地铁地图来说明。
•你见过绿线的新终点站吗?"
•红线每天早上这个时候都非常拥挤。"
•我住在橙线的尽头,对我来说还可以:自动扶梯直接把我送到
办公室。"
•我必须在这里换乘紫线。 明天见!"
当然,这一切都与地铁有关。 地下通道。 大都市地下铁路系统。 每条线路都有自己的颜色,每种颜色都是一条线路的名称。 当另一条线路建成时,问题就出现了:旧线路必须保持其颜色,而新线路应具有与旧线路看起来尽可能不同的颜色。 如果地铁中有两条或更多条新线路,情况会变得更加复杂。 新颜色不仅必须与旧颜色不同,而且它们之间也必须尽可能地不同。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。 通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
在本文中,我们将讨论一种选择这些颜色的数学策略。 顺便问一下,您会为图 1 中的真实地铁地图建议什么新颜色? 出于我们的目的,这张地图是理想的:它不仅有 14 种颜色,而且在不久的将来还将在该地铁中修建几条新线路(根据 [2],计划的扩展线路如图 6 所示)。 让我们使用这张地图来说明我们的策略——但读者可以将这些技术应用于他或她喜欢的任何其他地图(我们邀请读者分析图 2 中的伦敦地铁地图)。
测量颜色差异
为了最大化颜色差异——这里是在地铁地图中——我们需要一种方法来测量它们并客观地讨论颜色。 为此,我们使用一些坐标系(或色彩空间)将它们描述为数字元组。 例如,红、绿、蓝 (RGB) 色彩空间是众所周知的:在其中,每种颜色都由其 RGB 分量编码。 不幸的是,在 RGB 空间中,欧几里得距离与人们感知到的颜色之间的可见距离不成比例。 也就是说,RGB 空间不是感知均匀的——这正是我们所期望的。
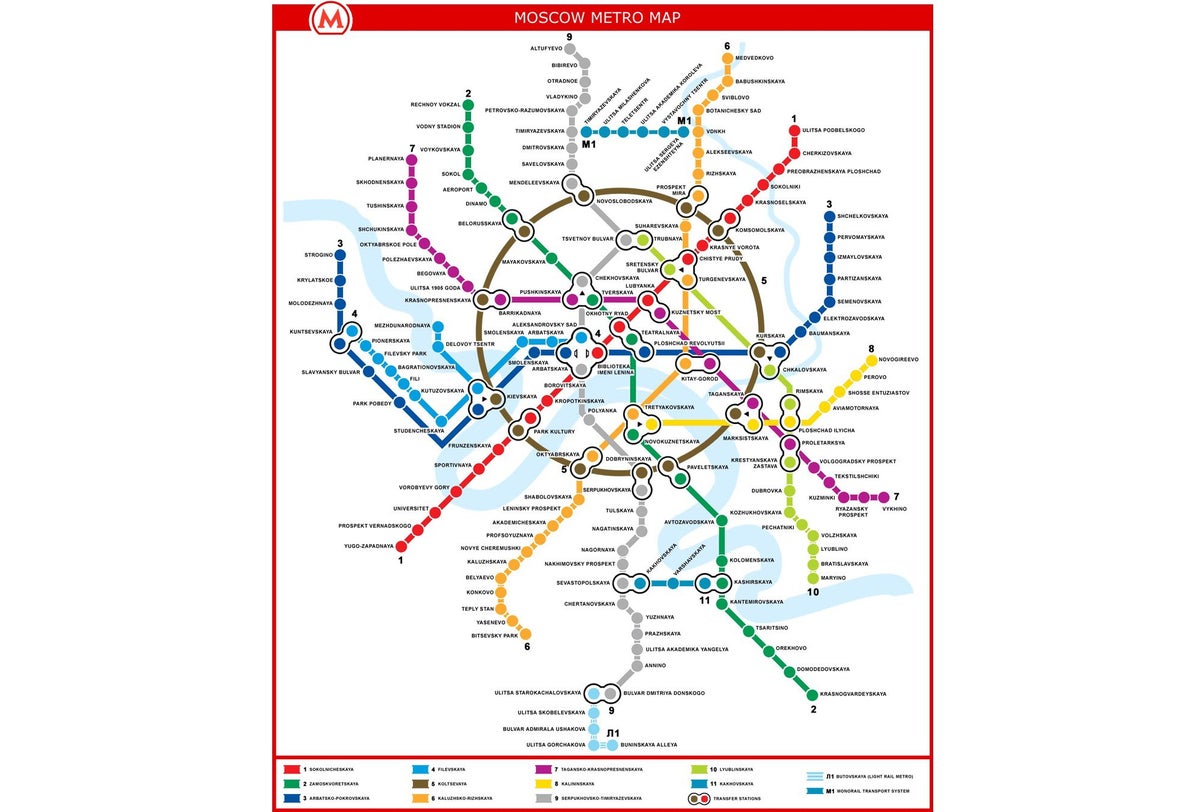
图 1. 您很可能已经认出这里是莫斯科地铁。
图片来源: 维基共享资源 (CC BY-SA 3.0)
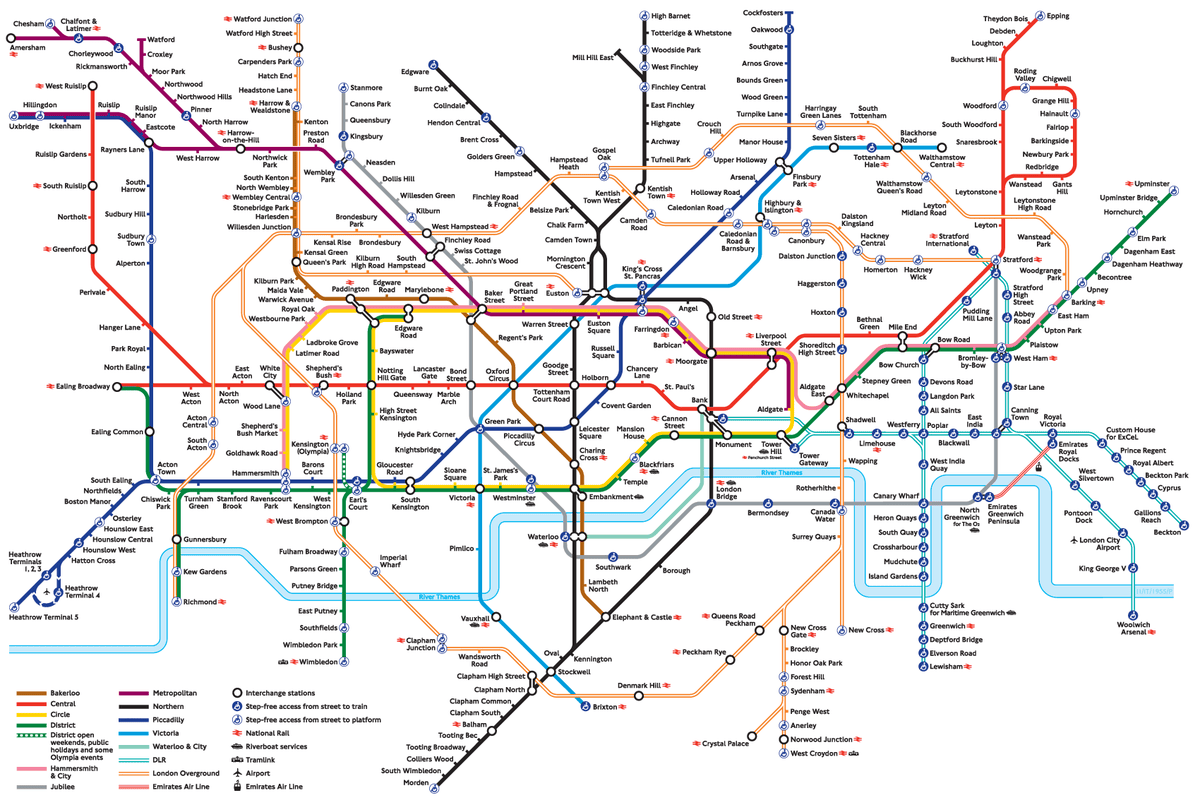
图 2. 伦敦地铁地图。
图片来源: 维基共享资源 (CC BY-SA 4.0)
1931 年,国际照明委员会 (CIE) 对数百名人类的视觉进行了测量。 根据这些数据,创建了几个色彩空间,以使关于颜色的交流变得容易和明确。 1976 年,CIE 建议使用两个近似感知均匀的色彩空间和色差公式。 这些空间因其官方推荐的缩写 CIELAB 和 CIELUV 而闻名。 在前者中,颜色由三个坐标描述:L(亮度)、α(红-绿尺度)和b(黄-蓝尺度)。 我们将使用这个空间用数字描述莫斯科地铁地图的颜色:它们的 CIELAB 坐标可以在表 1 中找到;图 3 显示了莫斯科地铁颜色在 CIELAB 空间中的立体图。
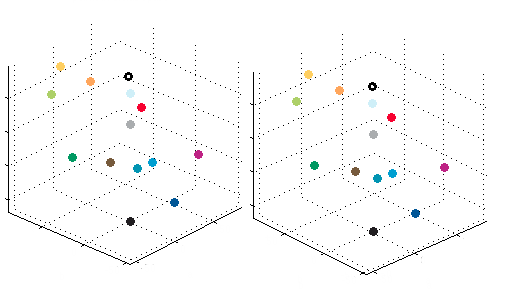
图 3. 莫斯科地铁地图颜色在其在 CIELAB 空间中的位置的立体图像。 L 轴是垂直轴,a 轴从西南向东北延伸,b 轴从东南向西北延伸。 (要查看 3 维图片,请同时用左眼看左图,用右眼看右图。) 图片来源:西蒙娜·F·格里菲恩
CIELAB 空间本身是无界的;但是,根据想要测量的内容,实际上只有一部分重要(例如,只有打印机可以打印的颜色或只有人眼可以看到的颜色)。 颜色的这种子集称为颜色色域。 Adobe 98 的色域在 CIELAB 空间中可以在图 4 中看到。为了使问题简单化,我们用多面体来近似这个色域。 因为 CIELAB 空间应该几乎是感知均匀的,所以欧几里得距离给出了 CIE 1976 色差公式 (CIE76)
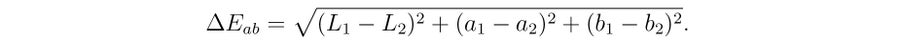
事实上,CIELAB 空间并非真正均匀。 特别是,在高 a 和 b 值下,过于简单的 CIE76 公式与颜色感知的实验结果相比,过分强烈地评估了色差。 这就是为什么提出了几个新的色差公式,其中最新的是 CIEDE2000 公式 (或 ΔΕ00)。
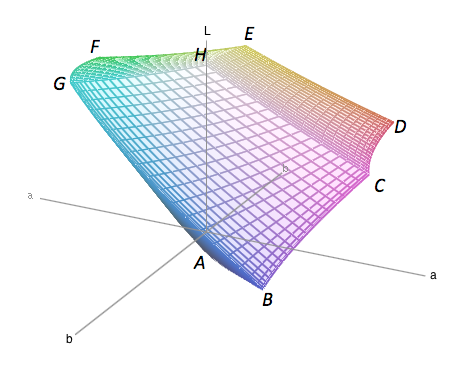
图 4. Adobe 98 的色域在 CIELAB 空间中。 我们通过取图中接近点 A、... H 的这个多面体的角点来近似这个色域。 图片来源:西蒙娜·F·格里菲恩
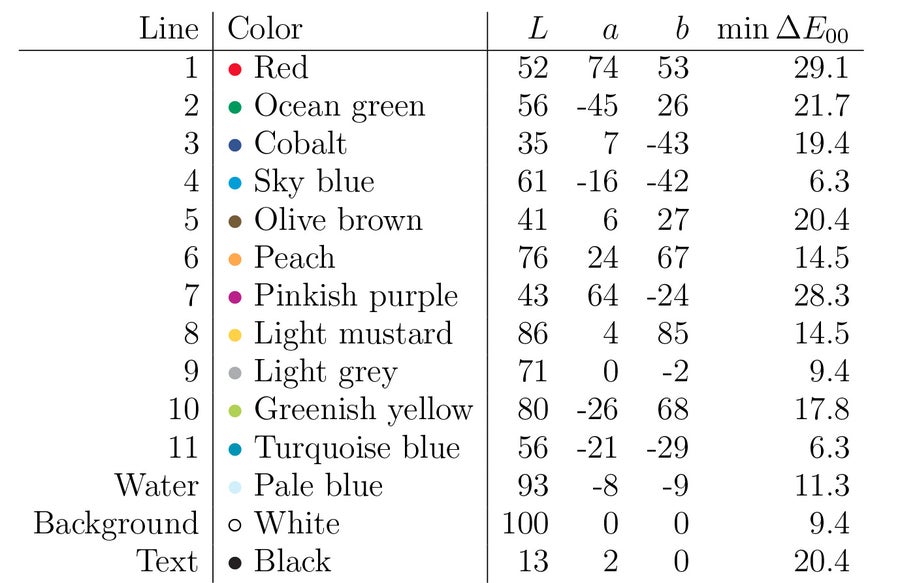
表 1. 莫斯科地铁地图上颜色的坐标。 颜色名称来自 [8]。 平均最小距离为 16.3。 请注意,一些最小距离是相同的;当两个点彼此最接近时,就会发生这种情况。 图片来源:西蒙娜·F·格里菲恩
2. 问题的数学公式
给定配备了欧几里得度量的 CIELAB 空间——甚至更好的是,CIEDE2000 色差公式——以及颜色色域 Γ(我们选择它是一个多面体),我们考虑一组现有的颜色 Ρ = {p1, . . . , pk} 在这个色域内,由它们的 CIELAB 坐标表示(例如,参见表 1)。 如果我们只想添加一条新线路,这将导致以下极大极小问题
问题 1(一种新颜色)。 我们如何找到一个 x ∈ Γ 使得

也就是说,从新颜色 x 到现有颜色的最小距离必须尽可能大,前提是颜色 x 保持在色域 Γ 内部或边界上。 如果我们想添加几条新线路,每条线路都有自己的新颜色,那么极大极小问题就变成了这样
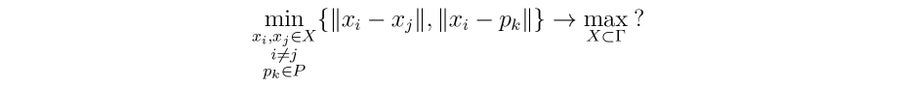
也就是说,我们最大化新颜色 x1, . . . , xm 之间的最小距离及其与旧颜色的最小距离。 或者,我们可以使用解决问题 1 的方法,逐个添加新颜色 x1, . . . , xm。 然而,这并不总是产生最佳结果。
3. 沃罗诺伊图方法
让我们考虑问题 1。 因为 CIELAB 空间是连续的(至少在原则上是这样),所以不可能“尝试色域中的所有点”来找到具有最大最小距离的点。 因此,如果只有有限数量的候选点要检查,那将会容易得多。 这可以通过使用沃罗诺伊图来实现。
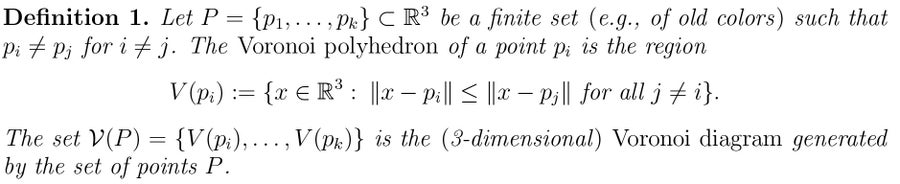
很容易证明,最大化问题 1 中最小距离的所需点 x 属于以下各项的交集
或者:三个沃罗诺伊平面,即沃罗诺伊多面体的三个面,
或者:两个沃罗诺伊平面和色域的边界平面,
或者:一个沃罗诺伊平面和两个边界平面,
或者:三个边界平面。
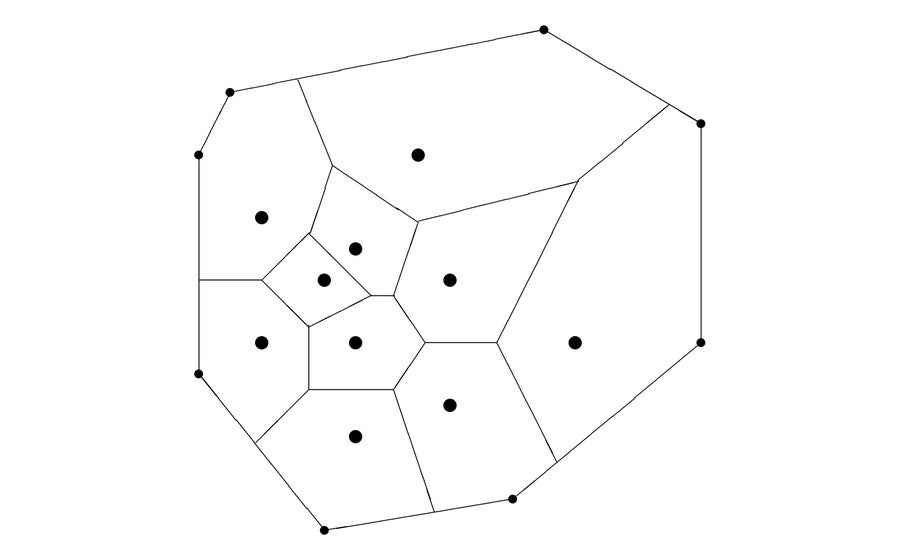
图 5. 二维沃罗诺伊图。 请注意,沃罗诺伊多边形的所有边都是连接图中两个点的直线的平分线的一部分。 图片来源:西蒙娜·F·格里菲恩
这意味着,一旦计算出这些候选点,就只需比较它们到现有点 pi ∈ P 的最小距离,然后取距离最大的点即可;事实上,结果集是有限且合理小的。 这是关于欧几里得距离的求解问题 1 的CIE76 沃罗诺伊方法。 在表 2 中,我们列出了使用此方法为莫斯科地铁逐个获得的五个新颜色。
很容易看出,如果存在感知均匀的色彩空间,沃罗诺伊方法将为极大极小问题 1 提供全局最优解。 然而,如今情况并非如此,因此让我们研究如何获得更好的估计。
由于 CIEDE2000 距离比欧几里得距离准确得多,我们可以通过比较 ΔΕ00 距离而不是欧几里得距离 ΔΕαb,从候选点中选择最佳点来改进我们的方法。 这是组合的 CIE76-CIEDE2000 沃罗诺伊方法。 当然,此方法不能单独解决关于 ΔΕ00 的问题 1,因为候选点是通过使用 ΔΕαb 找到的。 然而,这是一种使用 CIEDE2000 距离快速获得颜色的方法。 通过此方法为莫斯科地铁逐个获得的五个新颜色在表 3 中给出。 我们看到,与沃罗诺伊 CIE76 方法相比,这为我们提供了关于 CIEDE2000 距离的更好的解决方案:实际上,ΔΕ00 距离的下降速度要慢得多。
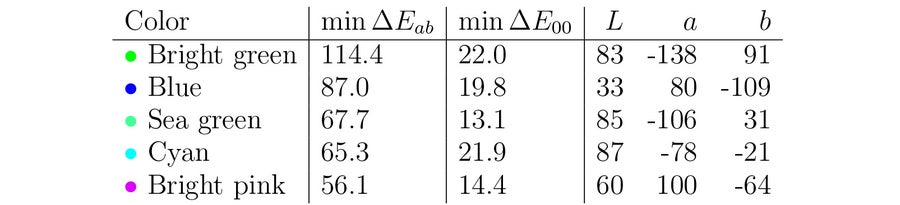
表 2. 我们使用 CIE76 沃罗诺伊方法(即,关于欧几里得距离求解问题 1)为莫斯科地铁的前五条新线路逐个找到的颜色。 我们在此处指示的最小距离考虑了表中较早出现的点。 请注意,最小 ΔΕ00 距离不一定在下降。 图片来源:西蒙娜·F·格里菲恩
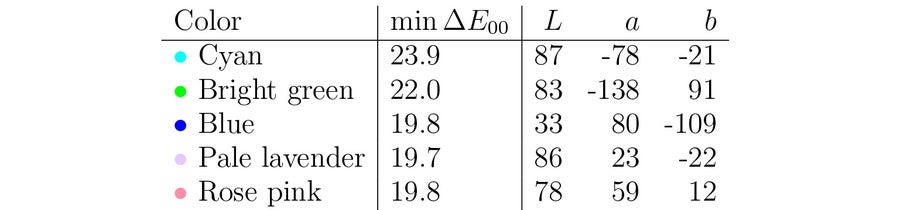
表 3. 我们使用组合的 CIE76-CIEDE2000 沃罗诺伊方法为前五条新线路逐个找到的颜色。 请注意,此处的距离是 CIEDE2000 距离,并且它们的下降速度比表 2 中慢得多。 图片来源:西蒙娜·F·格里菲恩
4. 单纯形法
我们也可以通过使用单纯形法来解决关于欧几里得距离的问题 2。 让我们在这里考虑颜色数量 m 为 2 的情况,这给我们提供了以下要最大化的函数,
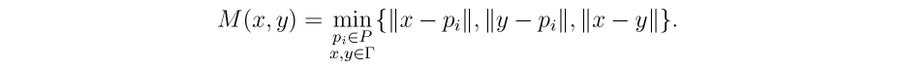
我们有 (x, y) ∈ Γ×Γ ⊂ ℝ6 。 让我们重写我们的问题:首先,放入一个额外的参数 x0 和两个向量 x, y 一起放入 x = (x0, x, y) ∈ ℝ7 ,现在最大化函数 M0(x) = x0 在所有满足约束条件 x ∈ ℝ × Γ × Γ 上
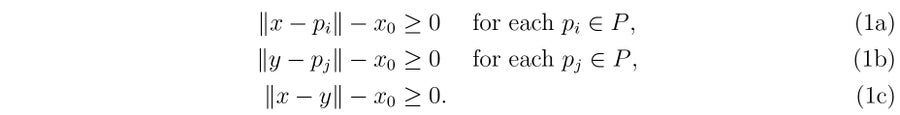
当然,使用更多关于 (x, y) 的约束来划定集合 Γ × Γ 的范围。 现在我们使用单纯形法来最大化我们的函数。
色域的边界给出了线性约束,非线性约束函数是方程 (1)。 因为单纯形法只给我们局部最优解,所以我们将其应用于一百万个随机初始点 (x0, x, y) ∈ ℝ7 (其中 x0 ∈ [0, 20] 且 (x, y) ∈ Γ × Γ)。 这些是关于 ΔΕαb 距离的局部最优解;现在让我们选择具有最大 ΔΕ00 距离的解。 这样,我们得到了两种颜色
亮水蓝色 • (84, -65, -12) 和淡粉色 • (86, 35, 7)。
它们与旧颜色和彼此之间的组合最小 CIEDE2000 距离为 22.7。 这比逐个 CIE76-CIEDE2000 沃罗诺伊方法的两步之后获得的最小距离要大。 因此,这为我们提供了更好的问题 2 的解决方案。 然而,这种方法非常耗时(随着 m 的增加,单纯形法将需要更多时间),因此速度快得多的沃罗诺伊方法是一个很好的替代方案。
5. 结论和讨论
我们得出结论,沃罗诺伊图方法(及其通过同时使用 CIE76 和 CIEDE2000 距离函数进行的改进)用于逐个添加新颜色,其给出的解决方案与用于一次找到两种或更多种新颜色的非光滑优化方法产生的解决方案相当。 对于所研究的莫斯科地铁地图来说,这是正确的。 当然,其他解决方案方案也是可能的,例如蒙特卡洛方法:在色域内随机生成新颜色 xi ∈ Γ 的测试点,而新颜色——或一组新颜色——是足够多次此类尝试中的极大极小最优解。 弹道方法的实现方式如下:首先,假设每个旧颜色 pi ∈ Γ 和所寻求的元组中的每个新点 xj 都带有正电荷(因此它们会根据库仑定律相互排斥)。 为了防止新点从色域 Γ 穿过其边界逃逸,在边界上最接近 xj 的点处为每个 j 放置一个可以忽略不计但为正的电荷。 通过从随机初始数据 xj (0) ∈ Γ 开始,电荷的配置 {xj (t)} 在多面体 Γ 内部演变,根据假设,多面体 Γ 充满了粘性介质,因此新点的运动减慢;它们迟早会在势的局部最小值附近被捕获(有关这两种方法的详细信息,请参见 [1])。
找到几种新颜色仍然不是在地铁地图上绘制新线路所需的全部内容。 显然,必须进一步考虑从旧线路到新线路的换乘配置——以便在新线路之间分配新颜色,从而在每个换乘站,相交线路的颜色尽可能不同。
突发新闻:在线投票。 官员表示,全长 16.8 公里、设有 8 个车站的科茹霍夫斯卡娅线计划于 2015-2016 年出现在莫斯科地铁系统中,参见图 6:从海绿色开始,该线路沿着绿松石蓝色延伸至红色。
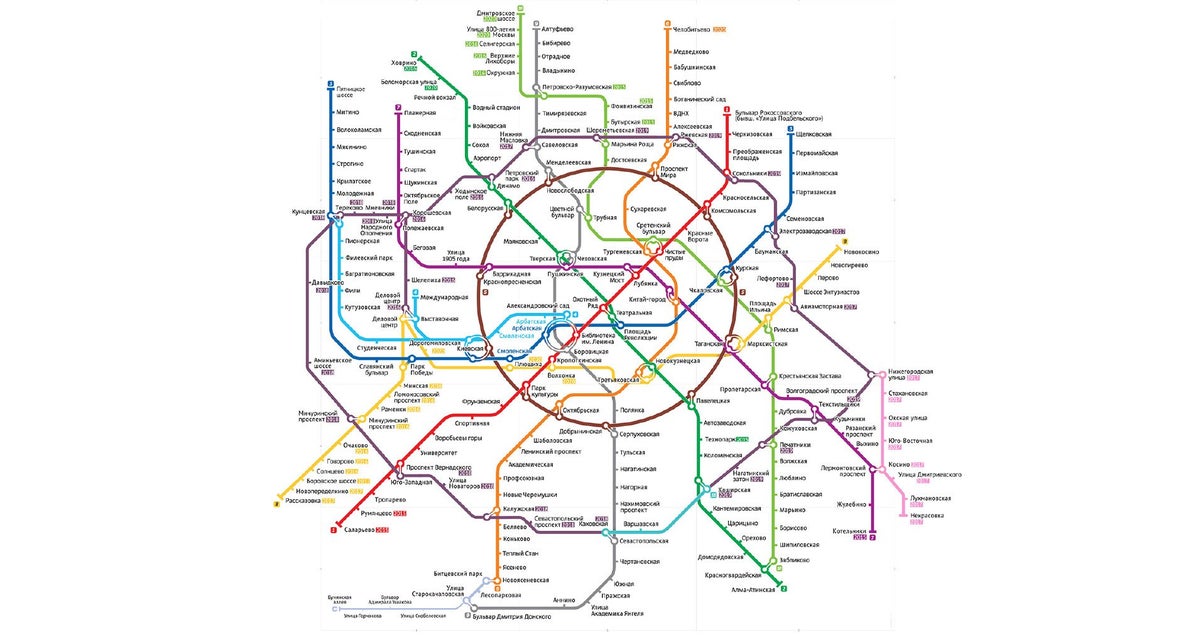
图 6. 莫斯科地铁的扩建计划。
图片来源: 维基共享资源 (CC BY-SA 3.0)
在 2014 年 10 月 20 日至 11 月 10 日举行的互动投票中,向预先注册的“活跃公民”提供了两种颜色供自由选择。 即,黑色和粉色被声称为色域中仅剩的尚未用于在莫斯科地铁地图上绘制线路的颜色(参见图 1)。 媒体报道称,多达 307,350 名活跃公民参加了在线投票; 71% 投票选择粉色,18% 倾向于黑色,而 7% 信任专家(如设计师、民族学家或心理学家)的选择。 最后,4% 的受访者要么提出了他们自己对新颜色的建议:绿松石色、橄榄色、珊瑚色等——甚至建议将地图上的那条线做成斑点状(参见 [12, 13])。
本文来自 《数学情报家》 ,经许可转载。 它最初于 2016 年 1 月 发表。
