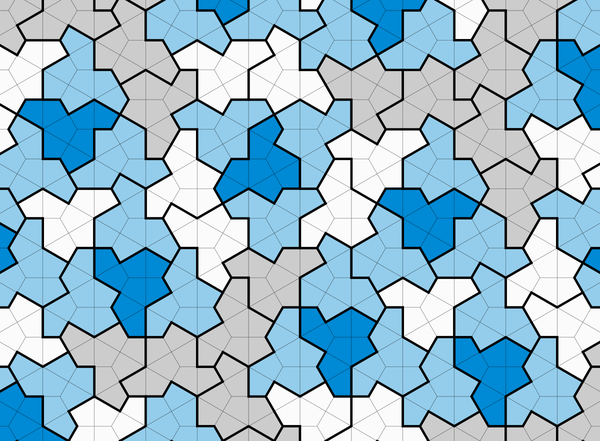
富有创意地铺设浴室地板不仅仅是让DIY家居装修者感到压力重重的任务。这也是数学中最难的问题之一。几个世纪以来,专家们一直在研究瓷砖形状的特殊属性,这些形状可以覆盖地板、厨房防溅板或无限大的平面,而不会留下任何缝隙。具体来说,数学家们对能够覆盖整个平面而永不产生重复设计的瓷砖形状感兴趣。在这些特殊情况下,称为非周期性平铺,没有你可以复制和粘贴以保持平铺继续进行的模式。无论你如何切割马赛克,每个部分都是独一无二的。
直到现在,非周期性平铺总是需要至少两种不同形状的瓷砖。许多数学家已经放弃了找到一种瓷砖解决方案的希望,这种瓷砖被称为难以捉摸的“爱因斯坦”瓷砖,其名称源于德语中“一块石头”的单词。
然后,去年11月,英国约克郡的退休印刷系统工程师大卫·史密斯取得了一项突破。他发现了一种13边的崎岖形状,他认为这可能是一种爱因斯坦瓷砖。当他告诉安大略省滑铁卢大学的计算机科学家克雷格·卡普兰时,卡普兰很快意识到了这种形状的潜力。卡普兰与软件开发人员约瑟夫·塞缪尔·迈尔斯和阿肯色大学的数学家海姆·古德曼-施特劳斯一起证明,史密斯的单块瓷砖确实无缝隙且无重复地铺满了平面。更棒的是,他们发现史密斯不仅发现了一种,而且发现了无数种爱因斯坦瓷砖。该团队最近在一篇论文中报告了他们的研究结果,该论文已发布到预印本服务器arXiv.org,尚未经过同行评审。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和想法的具有影响力的故事。
从美丽的图案到无法证明的问题
任何走过西班牙格拉纳达阿尔罕布拉宫令人叹为观止的马赛克走廊的人都知道平面铺贴所涉及的艺术性。但如此美丽之中也蕴藏着无法解答的问题——正如数学家罗伯特·伯杰在1966年所说,这些问题是可证明的无法证明的。
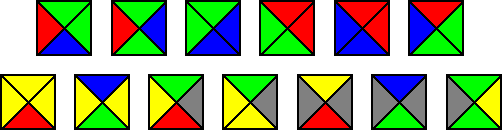
你能否创造一个无限的马赛克,只有相同颜色的边缘接触? 图片来源:Anomie/Wikimedia
假设你想用无限数量的正方形瓷砖铺设一个无限的表面。但是,你必须遵守一个规则:瓷砖的边缘是彩色的,只有相同颜色的边缘才能接触。
有了无限的瓷砖,你开始铺设。你找到了一种你认为会奏效的策略,但在某个时候,你遇到了死胡同。有一个你无法用现有瓷砖填补的缝隙,你被迫将不匹配的边缘放在一起。游戏结束。
但当然,如果你有合适的瓷砖和正确的颜色组合,你本可以摆脱困境。例如,也许你只需要一块所有边缘都是相同颜色的瓷砖。数学家会查看你的游戏并询问:“你是否可以通过查看一开始给你的彩色瓷砖类型来确定你是否会遇到死胡同? 这肯定会为你节省大量时间。”

非周期性马赛克。 图片来源:Claudio Rocchini/Wikimedia(CC BY-SA 3.0)
伯杰发现,答案是否定的。总会有一些情况,你无法预测是否可以在没有缝隙的情况下覆盖表面。罪魁祸首:非周期性平铺的不可预测、非重复的性质。在他的工作中,伯杰发现了一组令人难以置信的20,426种不同颜色的瓷砖,它们可以铺满一个平面,而颜色图案永远不会重复自身。更棒的是,用这组瓷砖物理上不可能形成重复的图案,无论你如何铺设它们。
这一发现提出了另一个问题,这个问题一直困扰着数学家:共同创造非周期性镶嵌所需的最小瓷砖形状数量是多少?
你能降到多低?
在随后的几十年里,数学家们发现了越来越小的瓷砖组合,可以创造非周期性马赛克。首先,伯杰发现了一种包含104种不同瓷砖的组合。然后,在1968年,计算机科学家唐纳德·克努特发现了一个包含92种瓷砖的例子。三年后,数学家拉斐尔·罗宾逊发现了一种只有六种瓷砖类型的变体——最后,在1974年,物理学家罗杰·彭罗斯提出了一个只有两种瓷砖的解决方案。
.png?w=900)
著名的、优雅的彭罗斯平铺仅使用两种类型的瓷砖来制作非周期性图案。 图片来源:Inductiveload/Wikipedia
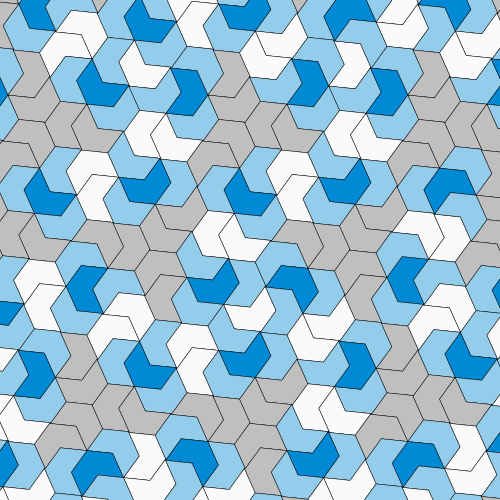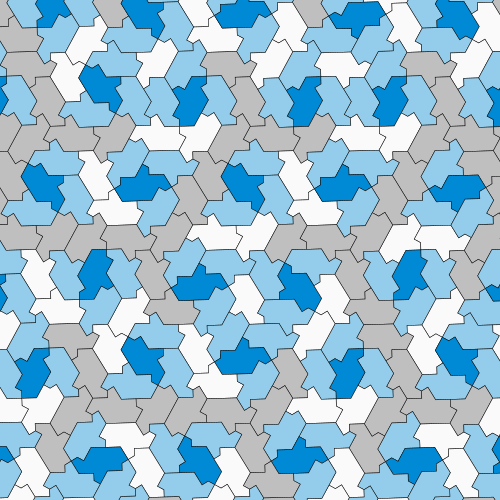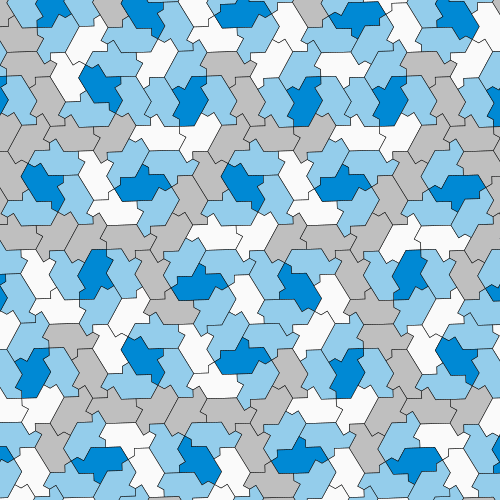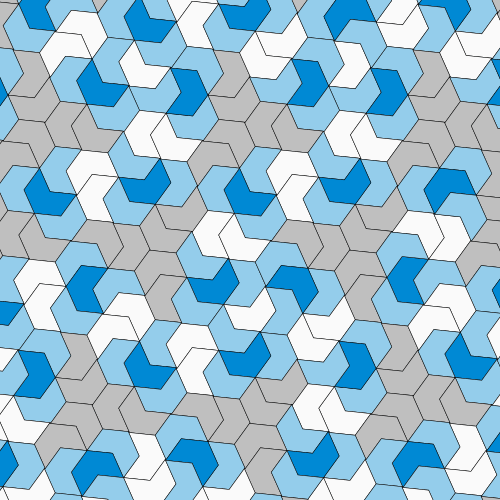
然后,进展停滞了。从那时起,许多数学家一直在寻找单块瓷砖解决方案,即“爱因斯坦”,但没有人成功——包括彭罗斯,他最终将注意力转向了其他难题。但64岁的退休人员大卫·史密斯并没有放弃。据《纽约时报》报道,他喜欢玩PolyForm Puzzle Solver,这是一款让用户设计和组装瓷砖的软件。如果一个形状看起来很有希望,史密斯会剪出几张纸质拼图来尝试。然后,在2022年11月,他偶然发现了现在著名的瓷砖,他称之为“帽子”,因为它像顶帽子——尽管卡普兰强调许多人认为它更像一件T恤。
_webp.jpeg?w=292)
史密斯的13边瓷砖看起来像帽子或T恤,具体取决于你的看法。 图片来源:David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss (CC BY-SA 4.0)
当卡普兰收到史密斯发来的带有“帽子”的电子邮件时,他很快就对此产生了兴趣。在软件的帮助下,他排列了越来越多的帽子形瓷砖,看起来它们似乎真的可以覆盖平面而不会形成重复的图案。
但是,如果他继续铺设瓷砖,这种重复的图案仍然可能会显现出来——也许只有当平面长达数光年时,才会出现冗余部分。研究人员需要从数学上证明这种平铺是非周期性的。卡普兰转向了迈尔斯和古德曼-施特劳斯,他们过去在平铺方面做了大量工作。
起初,他们对潜在的爱因斯坦瓷砖的简单性感到惊讶,因为“帽子”具有相当简单的13边形状。如果你之前问过古德曼-施特劳斯,难以捉摸的爱因斯坦瓷砖会是什么样子,“我会画一些疯狂的、弯曲的、令人讨厌的东西,”他告诉《科学新闻》。随着数学家们仔细观察这个形状,他们意识到他们可以调整边的长度,仍然可以创造出无缝的非周期性马赛克。这种形状打开了通往无数种爱因斯坦瓷砖的大门。
永不重复的图案
数学家需要确凿的证据来支持他们的主张。首先,他们使用了专家们几十年来一直依赖的方法来证明某些类型的瓷砖可以创造非周期性马赛克。但迈尔斯也超越了这些旧方法,创造了一种全新的证明方法,这种方法也可能对其他平铺有用。
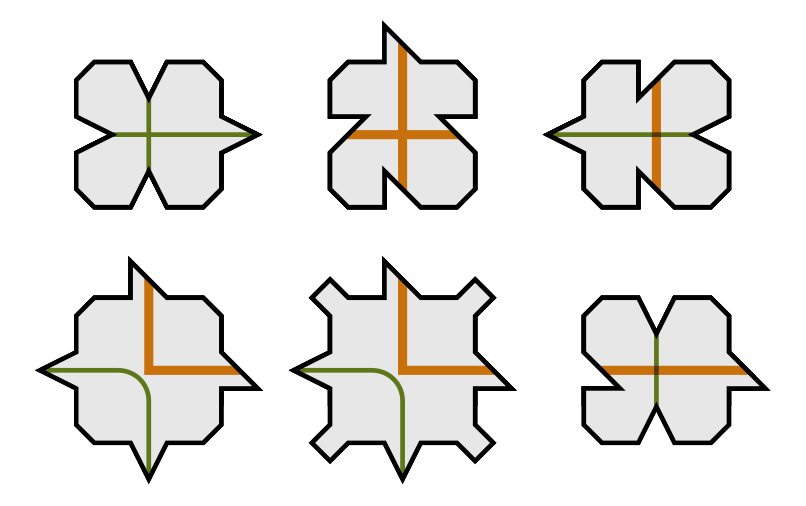
罗宾逊的六片瓷砖组合。 图片来源:Archibald/Wikimedia
使用罗宾逊1971年的六片瓷砖组合可以最好地解释经过验证的可靠方法。罗宾逊瓷砖上绘制的橙色和绿色线条的作用类似于先前无限正方形示例中的彩色边缘。这里的规则同样简单:只有当绿色和橙色线条平滑地延续时,才能将两片罗宾逊瓷砖彼此相邻放置。
遵循此规则会产生一个可识别的图案,该图案由越来越大的橙色正方形组成。如果你不断缩小,正方形会继续变大并相互交叉。这建立了一个层次结构,其中马赛克的每个部分都有其独特的位置。你不能在不违反规则和破坏结构的情况下移动或交换任何部分。这告诉我们,镶嵌必须是非周期性的。

罗宾逊平铺形成互锁的、分层的橙色正方形。 图片来源:C G Strauss/Wikimedia
卡普兰、古德曼-施特劳斯和迈尔斯能够证明史密斯提出的帽子形爱因斯坦瓷砖也具有类似之处。为了使瓷砖更易于使用,他们将帽子的崎岖边缘平滑成更易识别和有用的形状——例如,单片帽子瓷砖可以用三角形近似。他们还使用多块爱因斯坦瓷砖的簇来创建不同的形状。他们可以将四片帽子瓷砖排列成类似六边形的结构,两片瓷砖排列成五边形,另外两片瓷砖组合排列成平行四边形。然后,这四种平滑后的形状(每种形状都仅由爱因斯坦瓷砖组成)可以完全覆盖平面,形成图案。
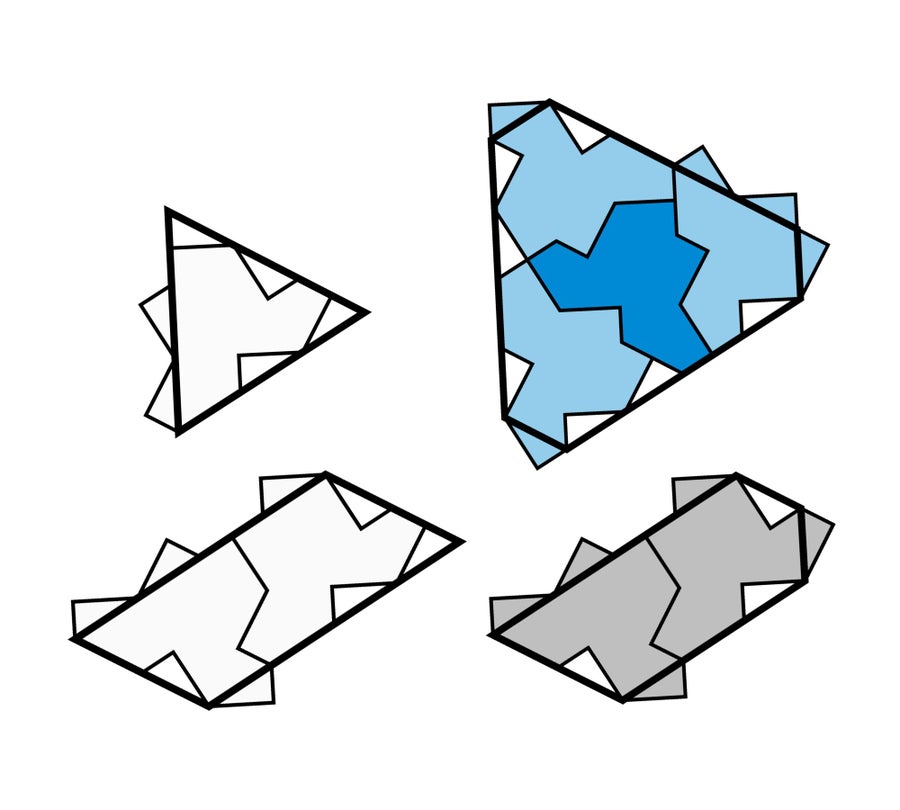
帽子形瓷砖可以组合成更大、更平滑的多边形,以证明瓷砖形状的非周期性。 图片来源:David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss (CC BY-SA 4.0)
数学家证明,这种平铺不包含重复的图案,因为就像罗宾逊的六片瓷砖组合一样,这四种特殊形状形成了层次结构。如果你将这四种爱因斯坦瓷砖簇(六边形、五边形、平行四边形和三角形)组合在一起,它们将不可避免地创建一个更大的版本,版本形状与其中一个相同的形状。然后,如果你将这些更大的形状组合在一起,你将创建更大版本的这些形状,依此类推。这个过程可以无限重复,从而产生层次结构。因此,整体图案无法分割成重复的部分。如果你只是将图案的部分滑动到另一个位置,那么总体结构将被破坏。
%5B2%5D_webp.jpeg?w=900)
爱因斯坦瓷砖的多边形簇形成分层的非周期性结构。 图片来源:David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss (CC BY-SA 4.0)
两种证明胜过一种
这个证明需要进行一些复杂的计算,因此这三位科学家寻求了计算机的帮助。他们免费发布了他们的计算机辅助证明,以便任何人都可以检查是否有错误。
但迈尔斯仍然不满意。他创建了一种新的证明非周期性的方法,这种方法可以通过手工完成,无需计算机,通过表明爱因斯坦帽子与更容易研究的其他著名平铺有关。这些相关的平铺由称为多边形钻石的形状制成,多边形钻石是由组合等边三角形形成的简单瓷砖。迈尔斯调整了一些爱因斯坦帽子的边缘,形成了两种不同的多边形钻石排列,它们遵循帽子相同的平铺图案——一种形状像人字形,另一种形状像六边形和菱形组合在一起。尽管它们的视觉差异,但这三种排列都具有相同的属性。如果数学家能够证明这两种多边形钻石平铺都是非周期性的,那么原始平铺也必须是非周期性的。
数学家可以通过将爱因斯坦瓷砖调整为两种更易于研究的形状来探测其属性。 图片来源:David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss (CC BY-SA 4.0)
值得庆幸的是,对于多边形钻石,该证明只是基本的数学问题。数学家可以用一个称为平移向量的量来表示多边形钻石排列的对称性。如果这两个新排列包含重复的图案,则其平移向量的长度应该彼此相关——具体而言,它们的比率应该是有理数。但相反,向量的比率为根号2——绝对是一个无理数——表明多边形钻石排列不是周期性的。因此,最初的帽子瓷砖确实是爱因斯坦瓷砖。
科学家们在他们的论文中解释说,迈尔斯的新证明方法也可能对其他平铺有所帮助。但就目前而言,专家和业余平铺爱好者都对拥有期待已久的爱因斯坦瓷砖感到兴奋。家居装饰的可能性真的是无限的。正如威廉姆斯学院的数学家科林·亚当斯告诉《新科学家》,“如果我现在要铺设浴室,我会把它放在我的浴室里。”
本文最初发表于《Spektrum der Wissenschaft》,并经许可转载。
编者注(8/2/23):本文在发布后进行了编辑,以更正拉斐尔·罗宾逊的名字和他的六片瓷砖组合的推出年份。