大多数人很少处理无理数——这样做是不理智的,因为它们会永远延续下去,并且准确地表示它们需要无限的空间。但是,诸如 π 和 √2 等无理常数(无法简化为简单分数的数字)经常出现在科学和工程领域。自古希腊以来,这些难以处理的数字一直困扰着数学家;事实上,传说希帕索斯因提出无理数的存在而被淹死。然而,现在,一个关于无理数可以被多好地近似的、近 80 年的难题已被解决。
许多人通过将无理数四舍五入为分数或小数来概念化它们:将 π 估计为 3.14,相当于 157/50,这导致了 3 月 14 日 Pi 节的广泛庆祝。然而,另一种近似值 22/7 更容易处理,也更接近 π。这就引出了一个问题:这些近似值的简单性和准确性是否会受到限制?我们是否可以以我们想要的任何形式选择分数?
1941 年,物理学家理查德·达芬和数学家阿尔伯特·谢弗提出了一个简单的规则来回答这些问题。考虑一个近似各种无理数的任务。首先,确定对于特定分母的分数,近似值应该有多接近。(记住,“分子”指的是分数的顶部,“分母”指的是底部。这里,所有的分数都已完全简化——例如,2/4 不算作分母为 4,因为它简化为 1/2。)你可能会决定,形式为 n/2 的简化分数可以近似任何无理数,其真值落在它们的 1/10 范围内——给近似值一个 1/10 的“误差”。分母为 10 的分数 n/10 在数轴上比分母为 2 的分数更接近,因此在这种情况下,你可能会将误差限制为仅 1/100——这些分数可以近似它们 1/100th 范围内的任何值。
支持科学新闻事业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您正在帮助确保有关塑造我们今天世界的发现和想法的具有影响力的故事的未来。
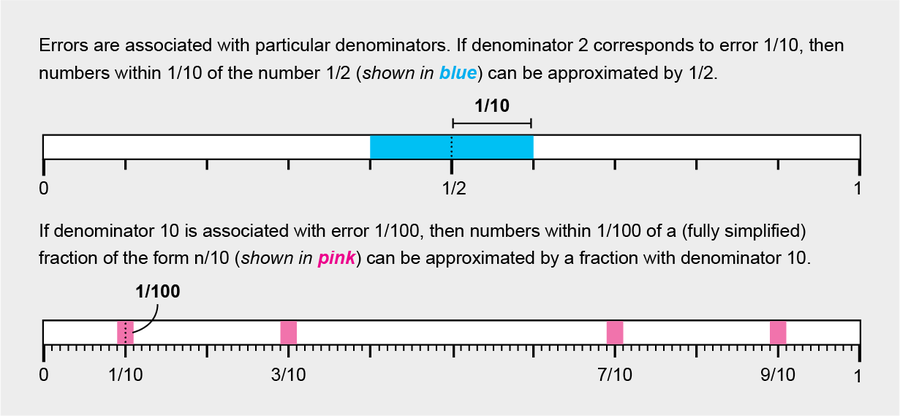
图片来源:Amanda Montañez
通常,较大的分母与较小的误差相关联。如果这是真的,并且有无限多的分母可以用来将一个数字近似到相应的误差范围内,那么通过增加分母,可以使近似值越来越好。达芬和谢弗的规则衡量了何时可以根据误差的大小来做到这一点。
如果选择的误差在总体上足够小,那么随机选择的无理数 x 将只有有限数量的良好近似值:它可能落在具有特定分母的近似值之间的间隙中。但是,如果误差足够大,那么将有无限多的分母可以创建一个良好的近似分数。在这种情况下,如果误差也随着分母的增大而缩小,那么您可以选择您想要的任何精度的近似值。
未证明
结论是,要么你可以任意好地近似几乎每个数字,要么几乎没有一个数字可以做到。蒙特利尔大学的数学家迪米特里斯·库库洛普洛斯说:“存在着鲜明的二分法。” 此外,您可以随意选择误差,只要它们在总体上足够大,大多数数字就可以通过无限多种方式近似。这意味着,通过将一些误差选择为零,您可以将近似值限制为特定类型的分数——例如,仅限分母为 10 的幂的分数。
尽管小误差似乎使近似数字变得更加困难,但达芬和谢弗无法证明他们的猜想——其他人也无法证明。奥地利格拉茨科技大学的数学家克里斯托夫·艾斯莱特纳说,该证明仍然是数论中的“里程碑式的未解决问题”,他研究过这个问题。直到今年夏天,库库洛普洛斯和他的合著者詹姆斯·梅纳德在发布到预印本服务器 arXiv.org 的论文中宣布了他们的解决方案。
达芬-谢弗猜想“在通常异常困难和复杂的数学领域中具有这种神奇的简单性,”牛津大学教授梅纳德说。他是偶然发现这个问题的——他是一位数论学家,但与大多数达芬-谢弗专家不在同一领域。(他通常研究素数——那些只能被自身和 1 整除的数。)约克大学的一位教授在梅纳德在那里的一次演讲后建议他解决达芬-谢弗猜想。“我认为他有一种直觉,即让稍微局外的人来做这件事可能会有好处,”梅纳德说。事实证明这种直觉是正确的,尽管它在几年后才结出果实。在最初的对话很久之后,梅纳德向库库洛普洛斯建议合作,因为他怀疑他的同事具有相关的专业知识。
梅纳德和库库洛普洛斯知道,该领域以前的工作已将问题简化为关于分母的素因数的问题——素因数是相乘在一起产生分母的素数。梅纳德建议将这个问题视为数字着色:“想象一下,在数轴上,将所有接近分母为 100 的分数的数字着色。” 达芬-谢弗猜想说,如果误差足够大,并且对每个可能的分母都这样做,那么几乎每个数字都将被无限多次着色。
对于任何特定的分母,只有部分数轴会被着色。如果数学家能够证明对于每个分母,着色的区域都足够不同,他们就可以确保几乎每个数字都被着色。如果他们还能证明这些区域是重叠的,他们就可以得出结论,这种情况发生了很多次。捕捉不同但重叠区域这一思想的一种方法是证明由不同分母着色的区域彼此无关——它们是独立的。
但这实际上并非如此,特别是当两个分母共享许多素因数时。例如,可能的分母 10 和 100 共享因数 2 和 5——并且可以被 n/10 形式的分数近似的数字与可以被 n/100 形式的分数近似的数字表现出令人沮丧的重叠。
绘制问题图
梅纳德和库库洛普洛斯通过将问题重新定义为数学家称为图的网络来解决这个难题——一组点,其中一些点通过线(称为边)连接。他们图中的点代表研究人员想要用于近似分数的可能分母,如果两个点有许多共同的素因数,则它们之间通过边连接。在允许的分母具有不需要的依赖性的情况下,这些图恰好有很多边。
使用图使两位数学家能够以新的方式可视化问题。“你需要获得的最大见解之一是忘记问题的所有不重要部分,而只专注于使 [它] 非常特殊的一个或两个因素,”梅纳德说。他说,使用图,“不仅可以让你证明结果,而且它真正告诉你一些关于问题中正在发生的结构性事情。” 梅纳德和库库洛普洛斯推断,具有许多边的图对应于一种特定的、高度结构化的数学情况,他们可以单独分析这种情况。
这对组合的解决方案让该领域的许多人感到惊讶。“普遍的感觉是这个问题离解决还很远,”艾斯莱特纳说。“使用 [图] 的技术是未来可能会被认为与——甚至可能比——实际的达芬-谢弗猜想更重要的东西,”德克萨斯大学奥斯汀分校的退休教授杰弗里·瓦勒说,他于 1978 年证明了该猜想的一个特例。
其他专家可能需要几个月的时间才能理解全部细节。“现在的证明是一个漫长而复杂的证明,”艾斯莱特纳说。“仅仅有一个引人注目的、辉煌的想法是不够的。有很多很多部分需要控制。” 这篇长达 44 页的密集技术数学论文,即使是顶级的数学头脑也需要时间来理解。然而,社区似乎很乐观。瓦勒说:“这是一篇很棒的论文。我认为它是正确的。”