关键概念
数学
几何学
分形
尺度
介绍
你有没有想过数学家研究什么——以及为什么?他们所做的大部分事情都复杂且难以理解,但分形艺术可能会让我们一窥究竟。数学家研究分形,这些是自然产生的图形,用于许多科学和技术领域。但你不必成为数学家也能欣赏它们的美丽。你知道你也可以创造一个吗?在这个活动中,你将拿出一些颜料来创作艺术品——并发现分形有多么常见。
背景
分形是几何图形。它们很难正式定义,但它们的特征和美丽使它们易于理解且引人入胜。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来有关塑造我们当今世界的发现和想法的具有影响力的故事。
一个特征是自相似性,它描述了分形如何在不同尺度上具有重复出现的模式。换句话说,当您放大时,您会发现最初看到的模式的较小版本。当您进一步放大时,您会发现该模式的更小版本,依此类推。这似乎会无限期地持续下去。
分形缩放的方式是另一个使其与传统几何图形(如直线、正方形和立方体)区分开来的特征。当您将线段的长度加倍时,原始线段将适合两次(或 21)其中,使线成为一维的。如果您将正方形边长加倍,则原始正方形将适合四次(或 22)在新、更大的正方形中,使正方形成为二维的。在立方体上执行相同的操作,原始立方体将适合八次(或 23)到新图形中,使立方体成为三维的。在分形上应用此操作,原始分形适合较大分形的次数可能是三、五或任何其他不是 2 的整数次幂的数字。这是分形的特征。它们具有分数维度,例如 8/5。
最后一个令人惊讶的事实:一些分形可以显示无限的周长,即使它们的面积是有限的。这是您可以在即将创作的艺术品中探索的内容。
材料
旧报纸(用于保护您的工作区域)
旧 CD 盒
指画颜料
纸巾或布
水
用于制作印花的纸张(手指画纸效果最佳。)
放大镜(可选)
准备
保护您的工作区。
拆卸 CD 盒,使您有两个松动的盖子。
将其中一个盖子平放面朝上放在您的工作区上,盖子的边缘在其下方。
步骤
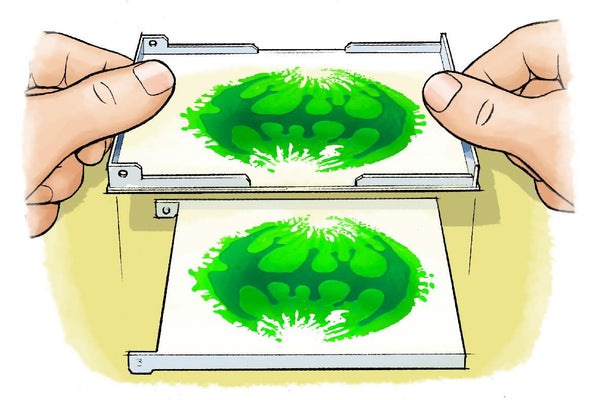
在盖子中心添加一滴葡萄大小的颜料。
将第二个盖子放在第一个盖子顶部,平面朝下,使颜料挤压在两个盖子的平面区域之间,并且盖子的边缘朝外。你注意到什么了?颜料会扩散吗?它形成什么类型的几何图形?
查看这个图形的周长。它比 CD 盒的周长长还是短得多?
当您轻轻地将两个盖子压在一起然后再次松开时会发生什么?几何图形会改变吗?会形成像悬崖或其他分支模式的图案吗?
您认为当您剥下顶盖时会发生什么?图形会改变吗?它会分支更多吗?您会得到两个图形,每个盖子上一个吗?如果是这样,它们会相同吗?
将盒子放回工作区,小心地提起顶盖。当您这样做时,尽量不要将盖子相互滑动,而是直接向上提起。
查看结果图形。您的预测正确吗?
选择一个图形并找到一个图案。然后,看看你是否能在你的图形中找到这个图案的更大或更小的版本。数学家将彼此的复制品——但其中一个可以比另一个更大或更小的图形或图案称为“相似”图形或图案。
将您的盖子平面朝下放在纸上以形成印花。您认为印刷的图形会是 CD 盒上图形的精确复制品吗?为什么是或为什么不是?
剥下盖子。再次,避免将盖子在纸上滑动。您的预测正确吗?您的印刷版本更详细还是更少?
分形是几何图形,其图案在多个放大级别上重复出现。您能在您的图形中找到图案的更小和更大的版本吗?如果可以,您就创造了分形!
如果您有放大镜,请使用它放大并查看是否可以在更小的尺度上找到相同的图案。在越来越小的尺度上重新出现的图案是分形的典型特征。
查看您分形的周长。想象一下在您的图形周围放置细绳,匹配其边缘的最小细节并切割细绳,使其刚好覆盖您图形的周长。然后想象一下拉伸这根细绳。它会比 CD 盒的周长长还是短得多?现在想象一下分形会分支成越来越小的细节。分形的周长会发生什么?它的面积会增长得那么快吗?这个分形还能放在 CD 盒上还是需要更大的表面?
制作和研究更多印花。完成印刷后,清洁盖子并通过添加新的颜料重复此过程。您的新图形与第一个图形有何相似之处,又有何不同?尝试组合不同的颜色,探索什么能产生最美丽的分形。
这些印花让您想到什么?它们像您知道的东西吗?
额外内容:仔细观察西兰花冠或罗马花椰菜。如果您在商店找不到,请在互联网上查找一些图片。您能看到相同的图案如何在不同尺寸下出现吗?
额外内容:环顾四周。你能在自然界中找到分形吗?看看树木、树叶、蕨类植物甚至云彩。这些也是分形吗?为什么是或为什么不是?
额外内容:一些分形由一个图形组成,该图形包含无限多个越来越小的自身版本。点击“更多探索”部分中列出的链接,了解谢尔宾斯基三角形。观看视频,因为它会放大。您看到图案如何在越来越小的尺度上无限重复自身吗?你能画一个谢尔宾斯基三角形吗?你能自己制作一个这种类型的分形吗?
额外内容:在互联网上查找一些计算机生成的分形和自然界中出现的分形的图像。有没有一些你觉得特别令人印象深刻的?
观察和结果
您是否在不同尺度上发现了重复出现的图案?您是否看到了分支图案的出现?
颜料喜欢粘在一起。当您首先将颜料挤压在盖子之间,然后释放或拉开盖子时,颜料内部以及颜料与塑料盖子之间的相互作用会产生令人印象深刻的分形。在光面纸上印刷可以让您重复此过程并创建显示更精细分支的图案。
虽然您的图形面积变化不大,但当添加越来越多的分支时,其周长增长很快。
分形在自然界中很常见。树木、树叶、蕨类植物、贝壳、闪电和云彩只是一些例子。分形不仅在我们周围,而且也在我们内部:我们的肺和血管显示出分形特征。分形数学可以帮助我们描述和量化这些结构。工程师也使用分形来创造新产品,例如手机天线。分形艺术是一种数字艺术形式,艺术家使用计算机生成的图像来创建复杂的物体。
清理
用肥皂水清洗所有设备。
更多探索 什么是分形?,来自分形基金会
地球上最令人惊叹的自然分形图案,来自《连线》 谢尔宾斯基三角形,来自莱斯大学
此活动与科学伙伴合作推出