你可能会惊讶地发现,你无法在不产生旋毛的情况下将椰子上的毛发梳平。 也许更令人惊讶的是,这个看似荒谬的主张,以及更滑稽的名字“毛球定理”,是数学分支——拓扑学中的一项重要发现。 抛开略显幼稚的幽默感不谈,这个定理在气象学、无线电传输和核能领域都有着深远的影响。
在这里,“旋毛”可以指秃斑,也可以指像《小捣蛋》角色阿尔法法头上的那种直立的绺。 当然,数学家在构建问题时不会提到椰子或旋毛。 用更专业的术语来说,可以将椰子想象成一个球体,而毛发则视为向量。 向量通常用箭头表示,它只是具有大小(或长度)和方向的东西。 将毛发贴着椰子表面梳平,就相当于形成切向量——即沿着其长度仅在一个点与球体相切的向量。 此外,我们想要一把光滑的梳子,因此不允许在任何地方分缝。 换句话说,球体上的向量排列必须是连续的,这意味着附近的毛发方向应该仅逐渐变化,而不是剧烈变化。 如果我们将这些标准结合在一起,该定理指出,无论你如何尝试将向量分配给球体上的每个点,都必然会发生一些“丑陋”的事情:会出现不连续性(分缝)、长度为零的向量(秃斑)或未能与球体相切的向量(阿尔法法)。 用完整的术语来说:球体上连续的非零切向量场是不可能存在的。
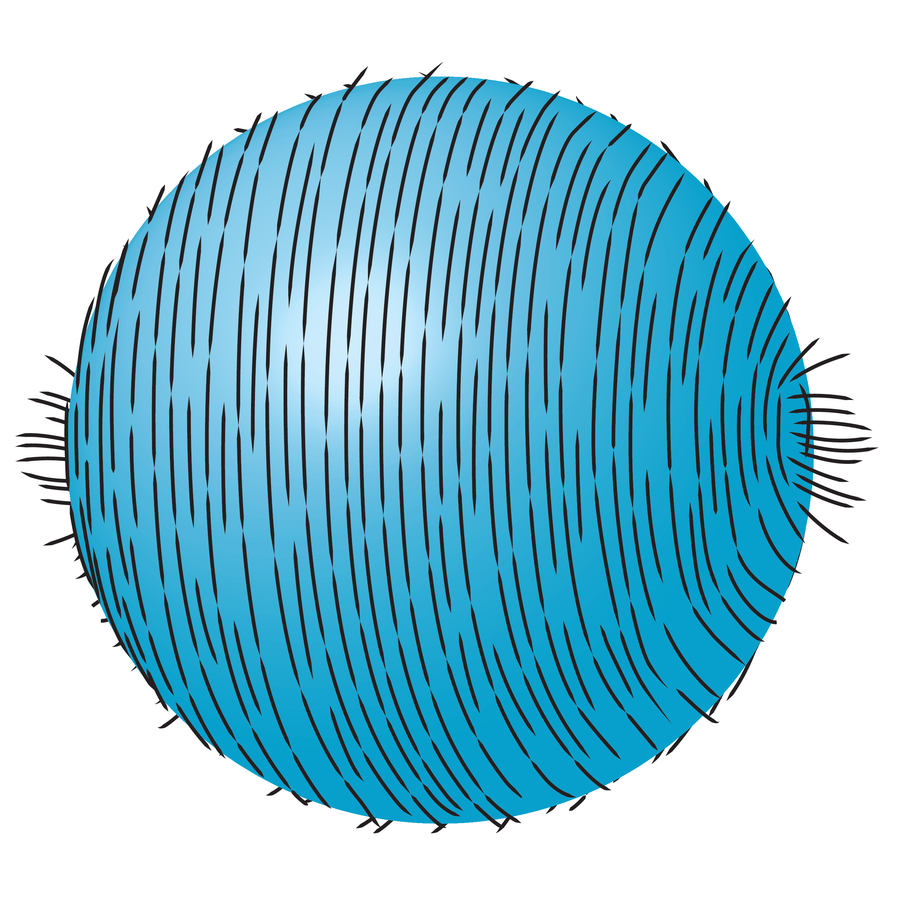
这个球体上布满了类似毛发的小线条,它们都朝同一方向梳理。两侧的簇状物演示了毛球定理。 图片来源:Buckyball Design
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。 通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和想法的、具有影响力的故事。
这一论断适用于各种毛茸茸的物体。 在拓扑学领域,数学家研究形状,就像在几何学中一样,但他们想象这些形状是由一种永恒的弹性橡胶制成的。 虽然这种橡胶能够塑造成其他形状,但它无法撕裂、融合或穿过自身。 如果一个形状可以平滑地变形为另一个形状而不做这些事情,那么对于拓扑学家而言,这些形状是等价的。 这意味着毛球定理自动适用于毛茸茸的立方体、毛茸茸的填充动物和毛茸茸的棒球棒,它们在拓扑学上都等价于球体。(你可以用一块橡皮泥将它们都捏出来,而不会违反橡胶规则。)
与球体不等价的东西是你的头皮。 头皮本身可以展平成一个表面,并像长毛地毯上的纤维一样朝一个方向梳理。 所以遗憾的是,数学不能为你的起床头开脱。 甜甜圈也与球体不同,因此一个毛茸茸的甜甜圈——毫无疑问,这是一个令人倒胃口的形象——可以被顺利地梳理平整。

这个甜甜圈形状上布满了类似毛发的小线条,它们都朝同一方向梳理,没有形成簇状物。 图片来源:Buckyball Design
这是毛球定理一个有趣的推论:地球上总会至少有一个点,那里的风不会沿着表面吹动。 风在全球范围内持续循环流动,其在地球表面每个位置的方向和大小都可以用与地球相切的向量来模拟。(向量的大小不需要表示物理长度,例如毛发的长度。) 这符合定理的前提,这意味着风必须在某处停止(形成旋毛)。 旋毛可能出现在气旋的中心或漩涡,或者可能是因为风直接向上吹向天空。 这个简洁的在线工具描绘了地球上最新的风流,你可以清楚地看到那些漩涡状的旋毛。
为了观察该定理的另一个奇特推论,可以随意旋转篮球。 球的表面上总会有一个点的速度为零。 同样,我们基于球上每个点的方向和速度,将一个切向量与该点关联起来。 旋转是一个连续的运动,因此毛球定理适用,并保证存在一个速度为零的点。 经过进一步思考,这似乎是显而易见的。 旋转的球体围绕着一条看不见的轴旋转,而该轴两端的点不会移动。 如果我们沿着该轴在球上钻一个小孔,以移除静止的点会怎样? 这样一来,似乎每个点都会移动。 这是否违反了毛球定理? 不,因为钻孔将球体变成了甜甜圈! 即使是孔异常细长的甜甜圈,也无视该定理的规则——矛盾得以避免。
从玩具场景转向实际应用——毛球定理实际上对无线电工程师施加了实际的限制。 天线根据设计选择在不同的方向上广播无线电波。 有些天线将其信号朝特定方向发射信号,而另一些天线则更广泛地辐射信号。 人们可能会倾向于简化问题,只制造在每个方向上同时发送等强度信号的天线,这些天线被称为各向同性天线。 但只有一个问题:拓扑学中的一个“毛茸茸”的事实表明,各向同性天线是不可能存在的。 想象一下从中心源发出的波球。 在离源足够远的地方,无线电波会表现出垂直于其传播方向的电场,这意味着该电场与波球相切。 毛球定理坚持认为,该电场必须在某处降至零,这意味着天线信号中存在干扰。 各向同性天线仅仅作为理论理想存在,我们用它来比较实际天线的性能。 有趣的是,声音传播的是另一种波,它不具有无线电波的垂直特性,因此可以制造出在每个方向上发出等强度声音的扬声器。
也许毛球定理最酷的应用与核聚变能有关。 核聚变能承载着巨大的希望——也许在未来的某一天——能够帮助缓解能源危机。 它有潜力产生大量的能量,而不会带来困扰化石燃料的环境问题,并且与传统的核裂变反应堆相比,放射性风险也大大降低。 简而言之,聚变反应堆首先使用氢等燃料,并将其置于高温高压下,这会将其分解成组成部分,形成等离子体。 等离子体是电子和其他带电粒子的云团,它们四处移动,偶尔融合在一起形成新的粒子,并在该过程中释放能量。
在建造聚变反应堆时,存在一个基本的工程障碍:如何容纳比太阳核心热 10 倍的等离子体? 没有任何材料能够承受如此高的温度而不分解成等离子体本身。 因此,科学家们设计了一个巧妙的解决方案:他们利用等离子体的磁性将其限制在强磁场中。 最自然的容器设计(想想盒子或罐子)在拓扑学上都等价于球体。 围绕任何这些结构的磁场都会形成连续的切向量场,而在这一点上,我们知道这种“毛茸茸”的结构会发生什么。 磁场中的零点意味着容器泄漏,这对整个反应堆来说是灾难性的。 这就是为什么领先的聚变反应堆设计——托卡马克装置——具有甜甜圈形状的腔室的原因。 国际热核聚变实验反应堆 (ITER) 大型项目计划在 2025 年前完成在法国建造新的托卡马克装置,相关人员声称他们的磁约束系统将是“有史以来建造的规模最大、集成度最高的超导磁体系统”。 这就是拓扑学在我们清洁能源未来中发挥的作用。
这是一篇观点和分析文章,作者或作者表达的观点不一定代表《大众科学》的观点。
