数学家在更高维度中重新发明轮子，解决数十年之久的几何难题

数学家们正在“重新发明轮子”，通过赋予它一种新的形状。他们新构想的轮子看起来像一个多维度的拨片，并且理论上可以以超出我们三维理解的方式滚动。这项突破通过展示如何在无法想象的维度中构建物体，解决了数十年之久的几何难题。

“这是一个令人惊叹的理论，”以色列爱因斯坦数学研究所的教授 Gil Kalai 说，他没有参与这项研究。结果证明，这些难以理解的物体可以在任何维度中构建，其尺寸仅为圆形或球体等更传统的滚动形状的一小部分。

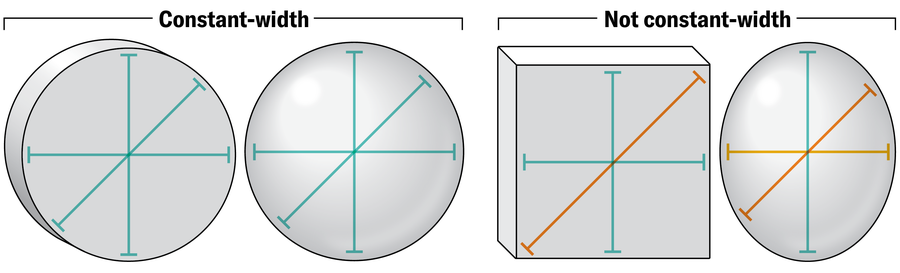
轮子之所以能滚动，是因为它们是具有“恒定宽度”的物体——从每个角度看，它们的宽度都相同。这种几何属性使轮子在移动时能够在两个平行平面（例如地面和汽车）之间保持恒定的距离。本质上，如果一个形状可以平稳滚动而不会晃动，那么它就具有恒定宽度。例如，将一个网球放在你平行的双手之间并旋转它——你会看到你的手永远不会更靠近或更远离，因为球具有恒定宽度的几何形状。像鸡蛋这样的椭圆形形状将无法通过该测试。

支持科学新闻报道

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅，您正在帮助确保未来能够继续报道关于塑造我们当今世界的发现和思想的具有影响力的故事。

圆形和球体是恒定宽度形状的简单、直观的例子，人类已经使用它们来促进运动数千年。这些是特殊类型的恒定宽度形状，称为“球体”——所有边界点与中心距离相同的形状。在二维中是圆形，在三维中是球体，并且这个概念延伸到我们无法轻易可视化的更高维度。

由于边界点都位于距中心点固定距离的位置，因此这些球体体积庞大：它们在任何维度中都具有恒定宽度形状的最大可能体积。但是，体积如此庞大并不总是理想的。在 20 世纪 80 年代，数学家 Oded Schramm 提出了一个问题：我们如何在任何维度中找到具有最小体积的恒定宽度形状？Kalai 说，这“是一个非常基本的问题”，数学家们一直有兴趣解决这个问题。“但没有人有任何探测它的方法。”

这个问题一直存在到今年 6 月，当时一个国际数学家团队提出了一种构建恒定宽度形状的新方法。研究人员的方法涉及无限数量的n维球体的交集，并在预印本服务器 arXiv.org 上以简洁的三页证明形式发布。“配方本身非常简单，”挪威科技大学数学教授、研究合著者 Andriy Bondarenko 说。虽然使用和分析这个配方相对简单，但研究人员花了数年时间才“[理解]为什么我们首先应该考虑这个配方。”

平面国里的轮子

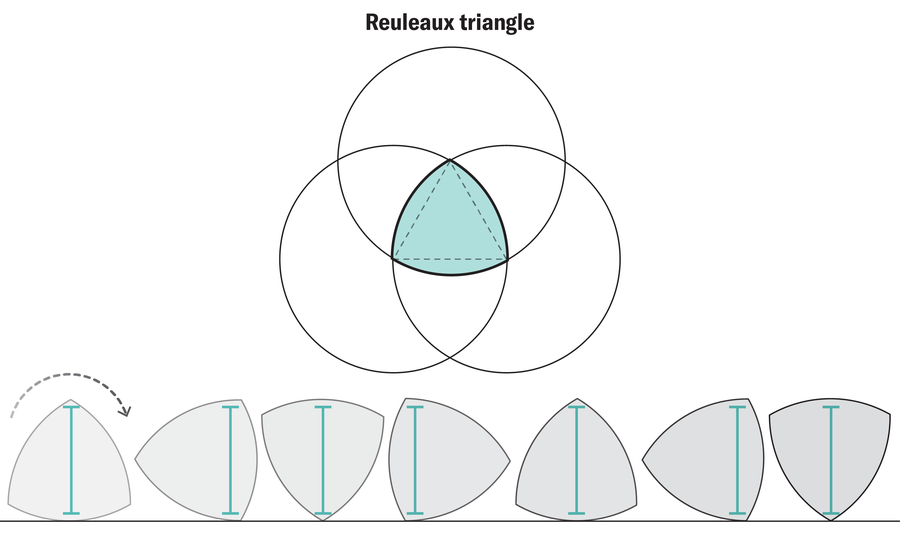
这项最新的工作率先研究了任何维度中的恒定宽度形状，但是在二维或三维中设计轮子本身并不是一个新问题。对于这些容易理解的较低维度，数学家们已经发现了许多体积更小的恒定宽度形状。在二维中，勒洛三角形具有恒定宽度形状的最小面积。您可以使用一种三向维恩图自行绘制此形状。首先，绘制一个等边三角形，然后在每个角周围添加三个半径相等的圆。在这些圆的中心，您会发现一个圆角形状，它像一个圆一样滚动，但尺寸只有圆形的一小部分。

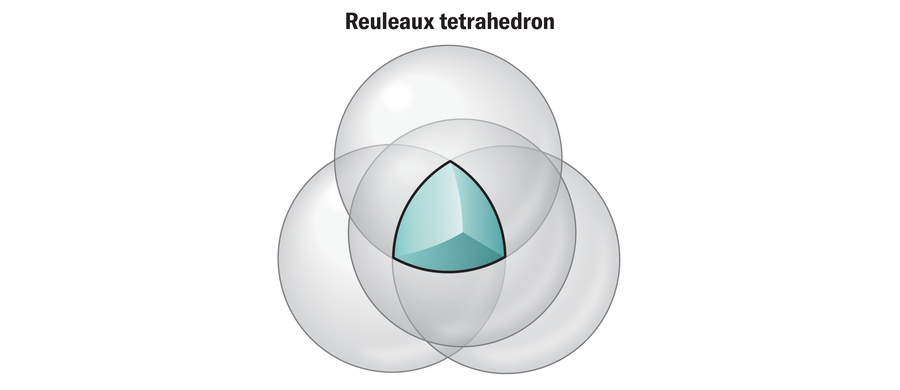
在三维中，您可以使用类似的方法：从正四面体（一种由四个等边三角形组成的形状）开始，并在其每个顶点添加一个球体。这些重叠球体中心形成的形状称为勒洛四面体。它并非完全恒定宽度——它很接近，但边缘伸出太多。但是，稍微打磨一下，就会产生恒定宽度的形状。这可以通过两种不同的方式完成，以形成两种略有不同的形状，称为迈斯纳体。

但是，这些形状背后的简单公式无法提供关于如何在四维或更高维度中构建的见解，这超出了人类的感知范围。“推广勒洛结构非常困难，”Bondarenko 说。“如果这很容易，以前就有人做过了。”

更高维度中的轮子

最新的工作通过扩展勒洛交集方法，提供了一种在任何维度中构建恒定宽度物体的通用算法。数学家团队使用了一种相关的类似维恩图的方法来产生所需的新形状——一个位于更高维度空间中心的几何异常小块。

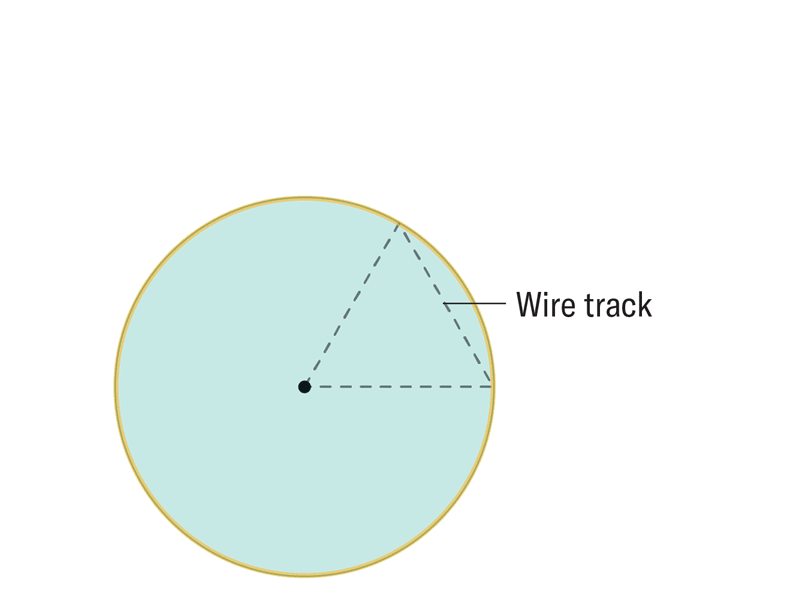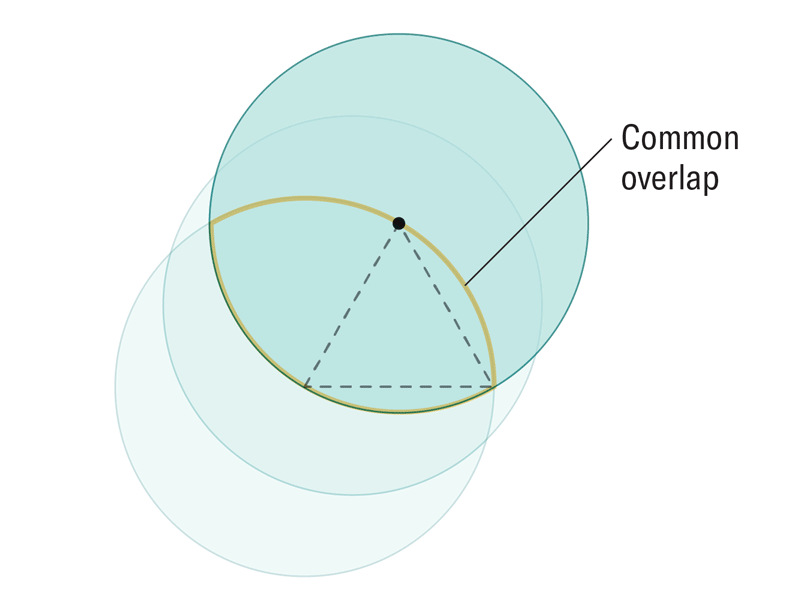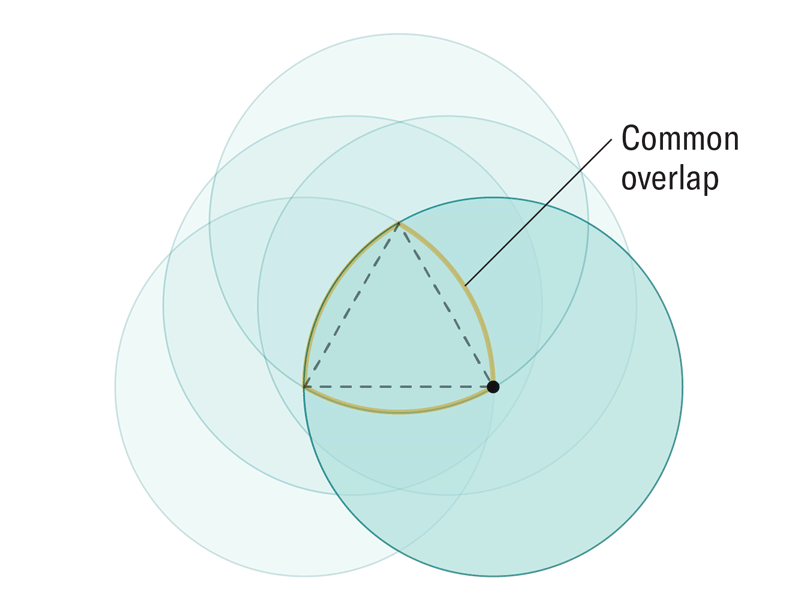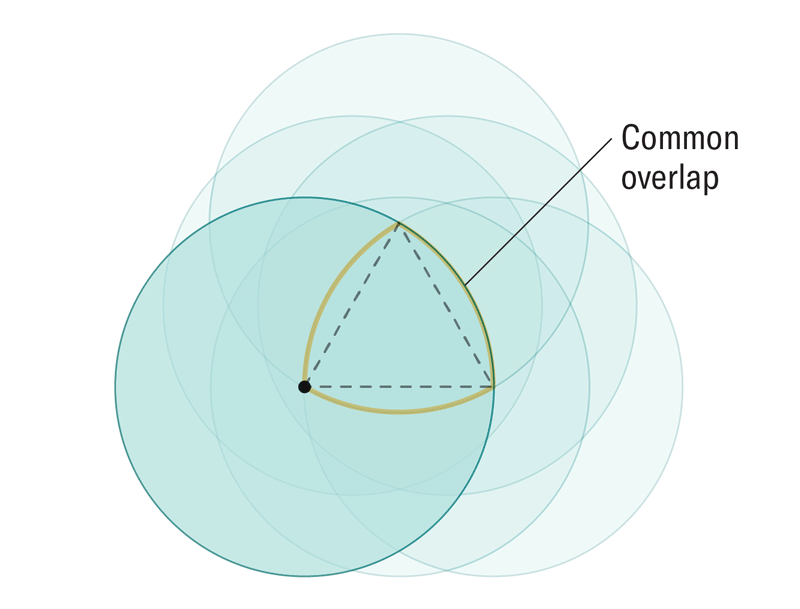
为了在二维中表示这一点，再次绘制一个等边三角形，然后在三角形的一个顶点周围绘制一个圆，半径与三角形的每条边一样长。然后想象移动该圆，使其中心点沿着三角形的轮廓移动，沿着每条边向上移动并经过每个顶点，然后再返回到起点。当圆移动时，有些位置它始终占据。移动圆的无限多个位置的交集形成了一个熟悉的形状：勒洛轮，它是勒洛三角形的推广。“通过这样做，您基本上得到了与勒洛三角形相同的结构，只是在这里我们取无限多个球体的交集，而不是仅仅三个或四个，”曼尼托巴大学的数学家和该研究的合著者 Andrii Arman 解释说。

这种简单、可计算的技术可以揭示任何维度中恒定宽度的物体，只要我们围绕其拖动圆的边界针对每个维度正确选择即可。根据这项新研究，在任何维度中选择这个边界都归结为一个基本配方。在二维中，我们围绕一个较小的四分之一圆而不是等边三角形来追踪圆。在三维中，我们将其进一步缩小，从球体的四分之一缩小到八分之一，并且这种模式通过增加 2 的幂扩展到更高的维度。在n维度中制作这样一个边界，并沿着它移动相应的n维球体，描绘出一个更高维度的维恩图，作者证明该维恩图的中心必须始终具有恰好为 2 的宽度，从而在任何维度中产生他们的新形状。

这种无限而非有限的构建形状的方法不仅确保了恒定宽度，而且还使得在更高维度空间中计算它们的体积变得简单明了。相比之下，先前的构造涉及估计多个变量的积分，而最新的工作仅涉及两个变量，而与形状的维度无关。“在高维度中估计体积真的很难，”Kalai 说，但“整个[证明]相当简单且非常优雅。”

新物体的体积比n维球体小 0.9ⁿ 倍，这意味着体积随着每个额外维度呈指数级减小。虽然当移动到更高维度空间时，形状的大小以越来越快的速度减小，但它们并不是保持恒定宽度的最小可能物体。Bondarenko 说，“据推测，迈斯纳体在三维中具有最小的可能体积”，并补充说，“我们的结果仅比此大 0.14%。”

Kalai 认为，使用无限级数在更高维度中创建这些形状“可能是[一个新]时代在恒定宽度集合研究中的曙光。”他总结说，随着最初的问题现在得到验证，“我们正处于未知的领域”，但凭借这些新方法，“我们有希望解决许多新问题。”