在过去的几年里,我搬了好几次家。一次又一次,我不得不测量房间或家具,然后检查我是否能像计划的那样安排好一切。当我们使用卷尺、折叠尺或直尺时,我们不会质疑我们测量的物体是否可测量。只要某物不是无限延伸的,我们就应该能够为其指定长度、面积或体积。这正是数学家们所假设的——直到 19 世纪末,一切都发生了变化。
长期以来,如果你想测量几何物体,你会像我搬家时那样做:拿出卷尺就开始测量。诚然,如果你想确定复杂曲线下的面积,任务就变得更加困难。随着 17 世纪微积分的发展,数学家艾萨克·牛顿和戈特弗里德·威廉·莱布尼茨以积分和导数的形式提供了新的测量工具,可以用来精确地确定几何图形的大小。但在 200 多年的时间里,没有人真正问过自己应该如何测量物体。
19 世纪末,当专家们试图将数学建立在稳定的基础上时,集合论成为了基石。该理论提出,一切事物——包括几何形状和复杂的微分方程——都可以追溯到基本集合。但是,如果几何形状只不过是集合,那么我们必须找到如何测量抽象集合的方法。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
让我们以数轴上 0 到 1 之间的区间为例,记为 [0, 1]。它包含无限多个实数,但是,为了我们的目的,我们假设它的长度对应于一厘米。数学家喜欢在没有单位的情况下进行计算,因此定义区间 [0, 1] 的长度为 1。类似地,区间 [0, 2] 的长度为 2,依此类推。
当然,专家们并没有简单地决定这一点,而是根据某些规则推导出来的。为了建立这些规则,他们试图总结长度、面积或体积等度量应具有的所有直观属性。即,空集的度量应为零;移动物体时,物体的度量不会改变;不重叠物体的度量等于各个物体度量的总和。从这三个简单的结论出发,可以定义各种维度,包括上述的长度维度,这符合我们的直觉。
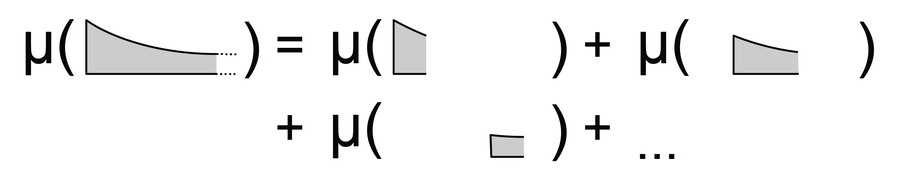
要计算不重叠集合的度量,您可以将各个集合的度量相加。
Stephan Kulla/Wikimedia Commons(CC BY-SA 3.0)
这个过程可能看起来相当繁琐:毕竟,您凭直觉就知道结果。然而,这种方法使得更广泛地测量量成为可能,即使是那些没有几何概念的量。
抽象量的度量
当数学家最初对度量感兴趣时,他们最初研究的是函数(即,定义两个变量x和y之间关系的表达式或规则)。您可能还记得中学时,可以通过积分来确定函数下方的面积。例如,您可以使用黎曼积分,其中您形成上限和下限和来确定曲线下的面积。例如,请参见下图中的蓝色条,它们表示如何将 x 轴划分为可以加在一起以计算总面积的小区间。
但是,如果函数极其复杂,会发生什么情况呢?例如,如果你看一下不连续的狄利克雷函数,那么用通常的积分概念就走不了多远。如果 x 是有理数,则狄利克雷函数 χ(x) 的值为 1。否则,该函数的值始终为零。绘制此函数的图形,您将看到 χ(x) 由沿直线 y = 1 和 y = 0 的无数个点组成。由于函数的图形仅由单独的、不相连的点组成,因此不可能使用黎曼积分。
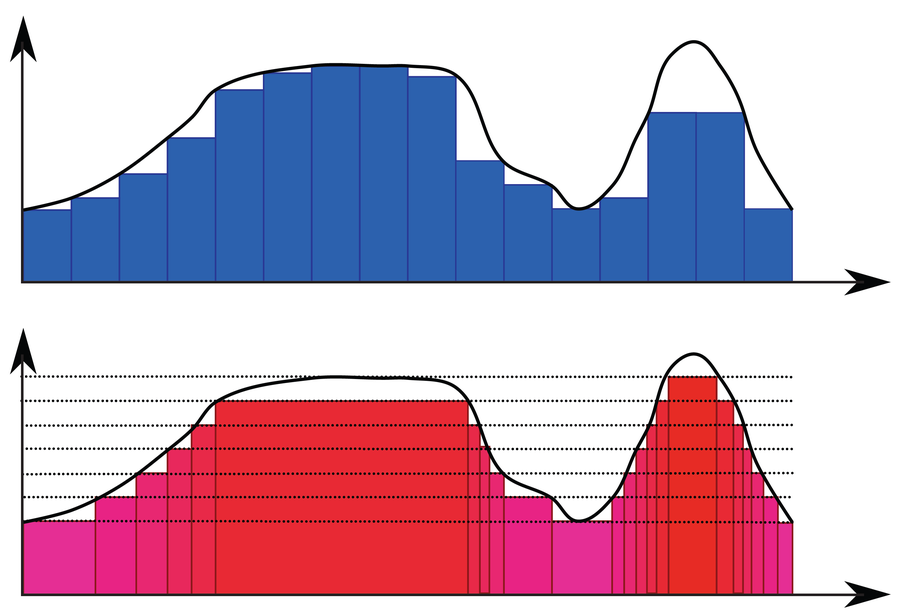
黎曼积分和勒贝格积分都通过分解来定义积分。黎曼积分垂直分解(蓝色),而勒贝格积分水平分解(红色)。
Svebert/Wikimedia Commons(CC0 1.0)
相反,您需要转向数学家亨利·勒贝格于 1902 年提出的勒贝格积分。在这种情况下,y 轴被划分为小区间——如上图中的红色条所示。要计算面积,您必须确定 x 轴上相应区间的宽度。
对于所有不像狄利克雷函数那样不连续的普通函数,勒贝格积分和黎曼积分提供完全相同的结果。勒贝格积分的优点在于它还可以为更复杂的情况指定面积。
因此,回到狄利克雷函数,在区间 [0, 1] 中,让我们使用勒贝格积分并将 y 轴划分为小段。函数的点仅位于 y = 0(对于无理数 x 值)或 y = 1(对于有理数 x 值),因此结果是 0 乘以范围 [0, 1] 中所有无理数的长度,加上 1 乘以 [0, 1] 中所有有理数的长度。此时,我们需要度量理论来为抽象集合指定长度:[0, 1] 之间的无理数和 [0, 1] 之间的有理数。由于只有可数个有理数(有关该陈述的证明,请参见下图和说明),因此它们的度量为零。[0, 1] 之间剩余无理数的度量因此必须为 1(因为 [0, 1] 中的所有实数加起来的度量为 1)。因此,狄利克雷函数在零和一之间的下方面积为 1 x 0 + 0 x 1 = 0。
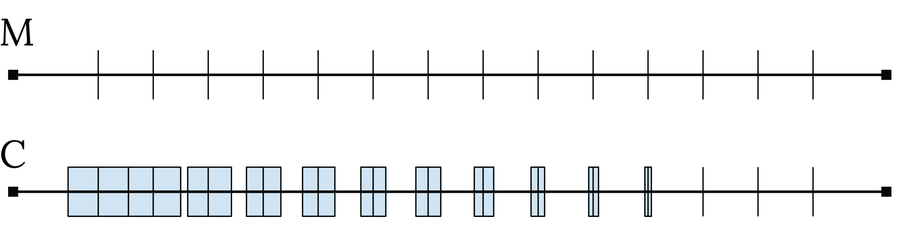
考虑集合 M = {m1, m2, m3, ..., mi, ...}。由于 M 包含可数个元素,因此可以用整数索引 i 对它们进行编号。要确定维度 μ(M),可以进行估计。为此,在每个 mi 周围形成一个小区间 Ii,其宽度 ε/(2i) 逐渐减小且任意小:Ii = [mi − ε⁄(2i+1), mi + ε⁄(2i+1)],并从中形成一个新集合 C = {I1, I2, I3,..., Ii, ...}。因此,C 类似于原始集合,只是它不包含单个点 m,而是包含小区间。总的来说,C 的度量必须至少与 M 的度量一样大:μ(M) ≤ μ(C)。现在可以通过假设 ε 选择得足够小以至于区间 Ii 永不重叠来计算 C 的度量。然后,该度量对应于区间的加法长度:μ(C) = ∑i∞ε/(2i) = ε。这意味着 M 的度量必须小于或等于 ε:μ(M) ≤ ε。由于 ε 可以选择为任意小,因此 M 的度量必须为零。这证明对于每个可数集,μ(M) = 0 成立。
马农·比肖夫/光谱科学
测量问题出现
勒贝格积分在 1902 年引发了所谓的测量问题。专家们想知道是否有可能为每个量指定一个度量。仅仅三年后,数学家朱塞佩·维塔利给出了一个令人沮丧的答案:不,有些集合非常不规则,无法测量。
当维塔利构造了一个具体的集合,任何类型的度量都失败时,他意识到了这一点:维塔利集,以他的名字命名。他从简单的开始,考虑了 0 到 1 之间的所有数字的集合。然后,他将这个集合划分为不同的区域:如果 a – b 的结果是有理数,则两个数字 a 和 b 最终会落在同一范围内。例如,所有自然数和所有有理数都在同一区域。在另一个区域中,有 0.2 + √0.2 和 0.3 + √0.2,依此类推。因此,维塔利将区间 [0, 1] 划分为(不可数)无限多个小部分。
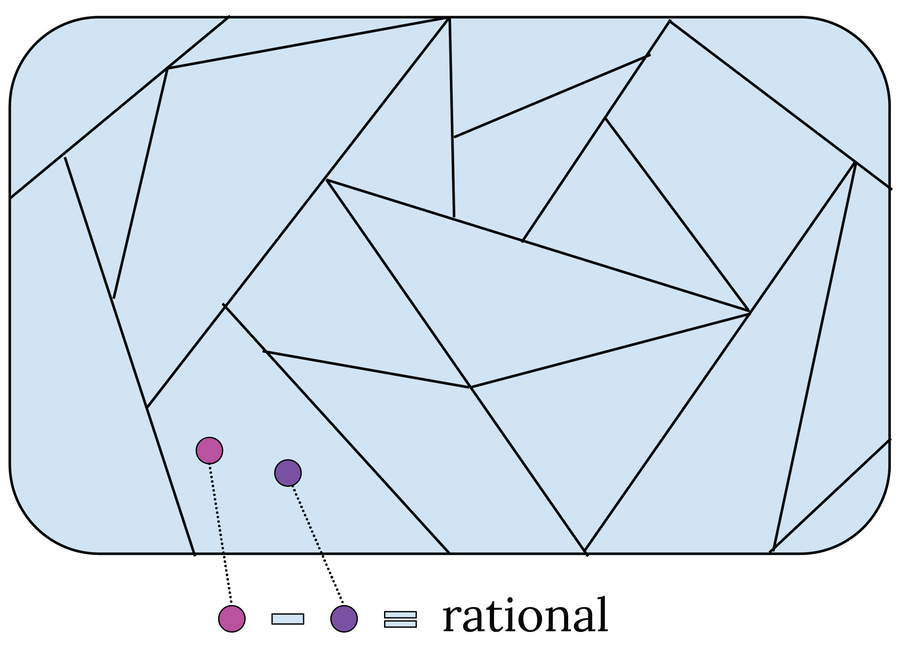
为了构造维塔利集,将区间 [0, 1] 分解为各个区域。如果两个数字(粉红色和紫色圆圈)的差是有理数,则它们在同一范围内。
马农·比肖夫/光谱科学
下一步,他从每个范围中精确选择一个代表 r,并将所有这些代表插入到一个新集合 V 中。因此,集合 V 包含不可数个元素,因为区间 [0, 1] 有不可数个无限个细分。然后,维塔利转向了一个技巧:他研究了如果集合 V 被有理数 p 移动会发生什么,p 的值介于 [–1, 1] 之间:Vp = V + p。结果,有理数 p 被添加到 V 中的每个元素 r 中。通过这种方式,维塔利生成了可数无限个集合 Vp,这些集合包含 [–1, 2] 之间的数字。原因是 V 包含 [0, 1] 之间的数字,而 p 添加了来自区间 [–1, 1] 的值。
这一切都非常技术性,但别担心;我们快到了!维塔利集 V* 包含所有 Vp,正如我们将看到的,它超出了度量理论的概念。我们知道 V* 的度量至少与区间 [0, 1] 的度量一样大(因为 V* 至少与 V 一样大,V 的范围为 0 到 1)。另一方面,维塔利集小于或等于区间 [–1, 2]。这意味着 μ ([0, 1]) = 1 ≤ μ(V*) ≤ μ([–1, 2]) = 3。因此,维塔利集的度量必须介于 1 和 3 之间。
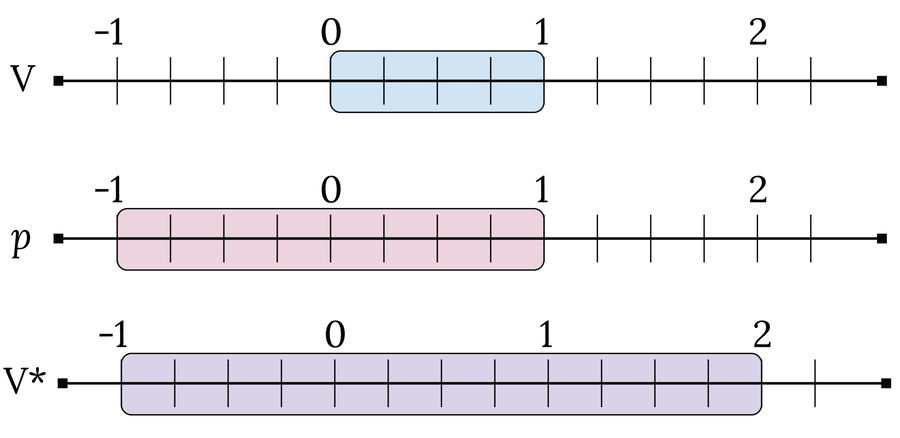
集合 V 的范围从 0 到 1,而值 p 的范围从 –1 到 1。因此,维塔利集 V* 的范围从 –1 到 2。
马农·比肖夫/光谱科学
现在您也可以直接计算维塔利集的度量:μ(V*) = ∑pμ(Vp),因为只有可数个 p。集合 Vp 包含 [p, 1 + p] 之间不可数个元素,因此 μ(Vp) 是一个大于零的有限数。事实上,所有 Vp 的大小都相同——p 的不同值仅表示平移,这与集合的大小无关。这意味着 μ(Vp) = μ(V)。因此,维塔利集的度量为 μ(V*) = ∑pμ(V),即一个常数 μ(V) 被无限次求和。这种计算的结果始终是无穷大——无论常数 μ(V) 有多小。这意味着:μ(V*) = ∞,这与上述不等式 1 ≤ μ(V*) ≤ 3 相矛盾。
总会存在不可测量的量
令人惊讶的结果并不意味着我们的数学运算有误。相反,维塔利集非常复杂,无法为其指定度量。因此,维塔利证明并非所有量都是可测量的;也存在“不可测量”的量。
这个结果本身就令人震惊。毕竟,维塔利集是有限的,并且仅包含实数值。如果将此结果转移到二维集合,您会得到更奇怪的结果:例如,您可以通过将球体分解为不可测量的集合来使球体的表面积翻倍。
幸运的是,不可测量的量极其罕见。例如,在物理学中,它们不会出现——毕竟,物体的分解受到原子大小的限制。您必须构造不可测量的量才能遇到它们。然而,它们又无处不在:即使在简单的数值区间中,也潜伏着不可测量的部分。事实证明,摆脱此类量并非易事。人们将不得不改变数学的公理——以及基础——以防止不可测量量的出现。
本文最初发表于《光谱科学》,经许可转载。
