“一个形状最少可以有多少个角才能铺满平面?” 数学家加博尔·多莫科斯在吃披萨时问我。他这个看似简单的问题是关于平铺的几何形状,也称为镶嵌——形状(称为瓦片或单元)的排列,这些形状填充表面,没有间隙或重叠。人类对镶嵌的痴迷至少可以追溯到古代苏美尔,在苏美尔,镶嵌在建筑和艺术中占据着突出的地位。但在思想家们摆弄瓦片的几个世纪里,似乎没有人认真思考过镶嵌的瓦片的最少顶点(线条相交的尖角)数量是否有限制。直到多莫科斯出现。追逐角越来越少的瓦片最终使他和他的小团队发现了一种全新的形状。
那是 2023 年的夏天,多莫科斯和我坐在黑狗餐厅的木制野餐桌旁,这是一个舒适的披萨和葡萄酒场所,离布达佩斯技术与经济大学只有几个街区,多莫科斯在那里担任教授。他穿过桌子,拿起一张纸质披萨菜单,翻过来,露出了空白的背面,并示意我拿一支笔。仲夏的天空呈现出橙色和靛蓝的色调,我用三角形填满了菜单。多莫科斯期待地看着。“你可以使用曲线,”他终于说道。我开始用圆形填满页面,当然,圆形本身无法填充空间。但多莫科斯眼前一亮。“哦,这很有趣!”他说。“继续,你可以混合形状。尽量保持平均角数尽可能低。”
我继续画下去。我的圆形页面充满了越来越绝望的、弯弯曲曲的形状。多莫科斯的玛格丽塔披萨早已消失,但他还没有完全准备好离开。快速浏览一下我粗略的图画还不足以确定其平均角数,更不用说可能的最小值了。但正确的答案一定比三角形的三个角要少——否则,这个问题就太无聊了。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于发现和塑造我们当今世界的想法的具有影响力的故事。
这个观察似乎让这位数学家感到满意,他透露真正的答案是二。“这是一个简单的问题,”他说。“但是 3D 呢?”
“对我来说,这是一种工具,可以合理地描述比简单地将多面体粘合在一起更广泛的物理相关事物。”——数学家海姆·古德曼-施特劳斯
现在,在披萨店的那个晚上过去一年多之后,多莫科斯有了答案。找到答案是一个激动人心、令人沮丧的挑战,最终促使他和三位同事发现了“软细胞”,这种形状可以组合在一起,完全填充平面或三维空间,并且角尽可能少。在二维中,软细胞有两个角,由曲线桥接。但在 3D 中,这些弯曲的、几乎有机的形状根本没有角。一旦研究人员确定了新的形状,他们就开始在各处看到它们——在自然界、艺术和建筑中。这些结果现已发表在期刊PNAS Nexus上。
尽管软细胞以前没有被数学家分类——没有人注意到或在学术论文中命名它们——但它们在艺术和自然界中比比皆是,从扎哈·哈迪德“曲线女王”的建筑,到斑马条纹的形状。多莫科斯的研究生克里斯蒂娜·雷戈斯在鹦鹉螺壳的腔室中发现了第一个天然 3D 软细胞,鹦鹉螺壳已成为展示数学和生物学融合的标志性物体。“它们一直就在我们眼前,”雷戈斯说。与如此著名的形状的联系让多莫科斯担心他的团队会被抢先。他发誓让他的合作者保密,直到他们的发现准备好发表。(它在九月发布。)在披萨课结束时,他甚至拿走了纸质菜单,将其折叠起来并放入口袋。只是为了安全起见。
史密斯学院的数学家约瑟夫·奥鲁尔克(未参与这项研究)表示,事后看来,软细胞的存在应该是显而易见的。但是,他说,想到提出这样的问题,“甚至想象你可以用没有顶点的物体来铺满空间”,这才是原创。“我发现这非常令人惊讶和非常聪明。”
阿肯色大学的数学家海姆·古德曼-施特劳斯是平铺方面的专家,他说:“对我来说,这是一种工具,可以合理地描述比简单地将多面体粘合在一起更广泛的物理相关事物。” “只要看看一杯啤酒中的泡沫,你就会知道他们正在研究一些东西。”
多年前,多莫科斯开发了一种数学工具,用于根据镶嵌的平均属性而不是单个单元的形状来描述镶嵌。这个想法源于对天然马赛克(如破裂的岩石表面)的研究。使用平均值可以捕捉镶嵌的本质,而不会施加不自然的刚性。
当多莫科斯和雷戈斯探索控制马赛克平均属性的规则时,他们意识到了一件事:似乎不可能将每个瓦片的平均顶点(角)数降到两个以下。由此,人们很容易意识到,单瓦片——仅用自身副本填充平面的瓦片,例如蜂巢的规则六边形或棋盘的方块——不可能少于两个顶点。以前没有人认识到这条规则。
当多莫科斯和雷戈斯找不到任何关于该主题的先前工作时,两人意识到他们手头有一些有趣的东西。但是,当涉及到将他们的发现转化为正式的数学规则时,他们感到几何学知识不足。他们招募了同样在布达佩斯技术与经济大学工作的几何学家阿科斯·G·霍瓦特来帮助他们。
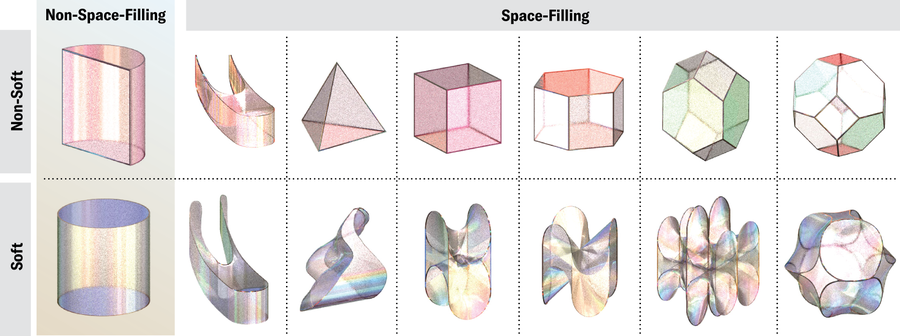
霍瓦特很快设计出一种算法,可以将平面的多边形平铺变形为仅具有两个顶点的形状的平铺。利用它,该团队从三角形、六边形和矩形的规则平铺中设计出圆形、柔软的双顶点瓦片。他们使用的六边形瓦片看起来像六边形,其中两个角被拉伸出来,其余部分被磨成圆形的小突起。从正方形衍生的瓦片更加多样化。一种看起来像变形的正方形,但其他瓦片类似于木瓦、鱼鳞、扁豆和鲸鱼的尾叶。从三角形衍生的两种类型的瓦片看起来有点像小山和船帆。
然后,多莫科斯说,“我们开始幻想 3D 中会是什么样子。”
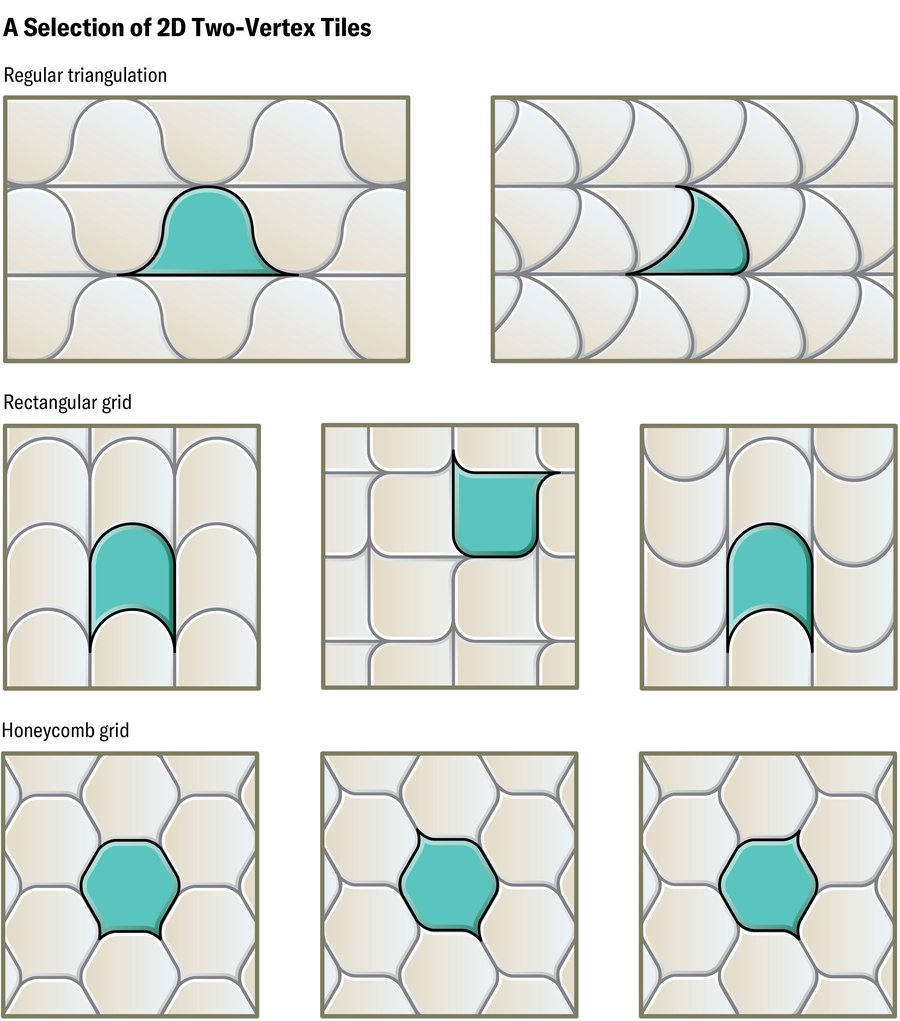
Jen Christiansen;资料来源:“软细胞和贝壳的几何形状”,作者:加博尔·多莫科斯、阿兰·戈里利、阿科斯·G·霍瓦特和克里斯蒂娜·雷戈斯;2024 年 2 月 6 日;arXiv:2402.04190(瓦片参考)
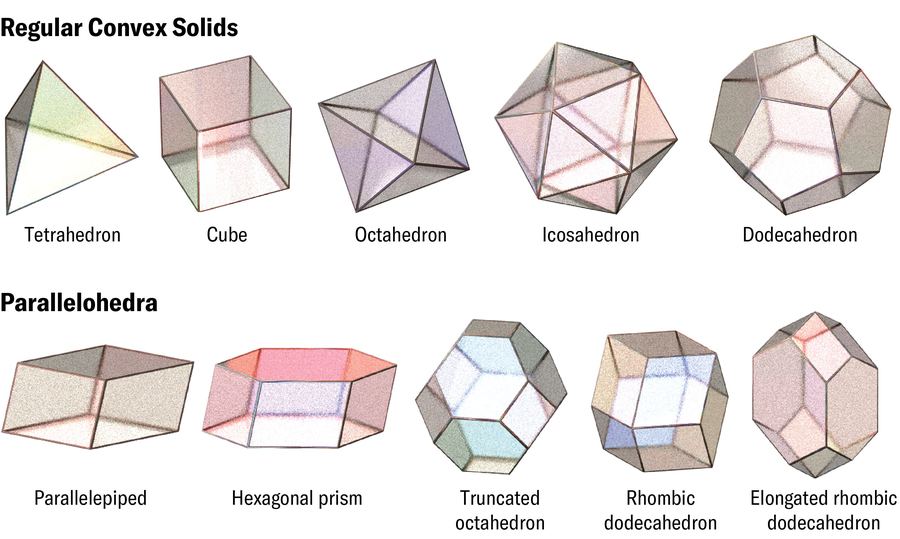
至少从柏拉图时代起,人们就一直在想象 3D 镶嵌。他围绕五个正凸多面体(四面体、立方体、八面体、二十面体和十二面体)的镶嵌构建了他的宇宙模型。柏拉图认为,前四种形状的镶嵌应该构成土、气、水和火的古典元素。十二面体是宇宙的物质。柏拉图的错误不仅仅在于这种深奥的宇宙学。只有立方体实际上可以作为单瓦片填充 3D 空间——用一个形状的精确副本——而没有间隙和重叠(除非空间本身是弯曲的)。但是,挤压和拉伸成立方体的平行六面体(面为六个平行四边形的形状)也可以填充空间。1885 年,俄罗斯晶体学家叶夫格拉夫·费多罗夫编目了一组五种形状,称为平行多面体——可以无任何旋转地堆叠在一起的 3D 形状。这些形状包括立方体和蜂巢中常见的六棱柱,以及更深奥的菱形十二面体、拉长十二面体和截角八面体。
所有这些形状都是具有平面和直边的多面体。但是,具有曲线的 3D 形状也可以填充空间——尽管现成的例子只是稍微弯曲并且具有明显的角。具有启发意义的是,已知的例子都源于对自然的疑问,而不是抽象数学。1887 年,英国数学家威廉·汤姆森(也称为开尔文勋爵)提出了一个难题:体积相等的细胞或气泡的什么排列方式可以最大限度地减少它们之间界面的表面积?换句话说,什么是最佳泡沫?
Violet Frances
开尔文的第一个解决方案是略微变形的截角八面体的镶嵌。在 1994 年的一篇论文中,当时都在都柏林圣三一学院的物理学家丹尼斯·韦尔和罗伯特·费兰用两种不同的变形多面体的镶嵌击败了开尔文的结构。2018 年,由塞维利亚大学的路易斯·M·埃斯库德罗和西班牙综合系统生物学研究所的哈维尔·布塞塔领导的一个生物物理学家团队发现了一种名为盾片的形状,类似于变形的蜂巢,人体的上皮细胞会呈现这种形状,以便在需要弯曲和弯曲的组织中进行最佳堆积。尽管如此,似乎没有人问过空间填充固体可以有多少个角。匈牙利团队向 3D 的飞跃最初是一种信念的飞跃。“我们一点头绪都没有。甚至没有预感,”多莫科斯说。

Violet Frances
当三人最终确定了一个只有两个角的空间填充 3D 形状时,多莫科斯认为他们找到了答案。“我完全痴迷于这件事,”他说。“我写了一篇论文,证明三维空间中的最小角数是两个。” 这个证明源于多莫科斯认为微不足道的一个简单假设。但是,随着几个月过去了,他慢慢开始意识到这个假设并非那么微不足道——甚至可能是错误的。“他想在圣诞节、新年夜,以及之后更晚的时候把这篇文章发给我和阿科斯,”雷戈斯回忆说,忍俊不禁。“然后他找到了一个零角的例子。就是这样。” 这种形状本身就是一个证明:在三维空间中,可以用根本没有角的物体来镶嵌空间。
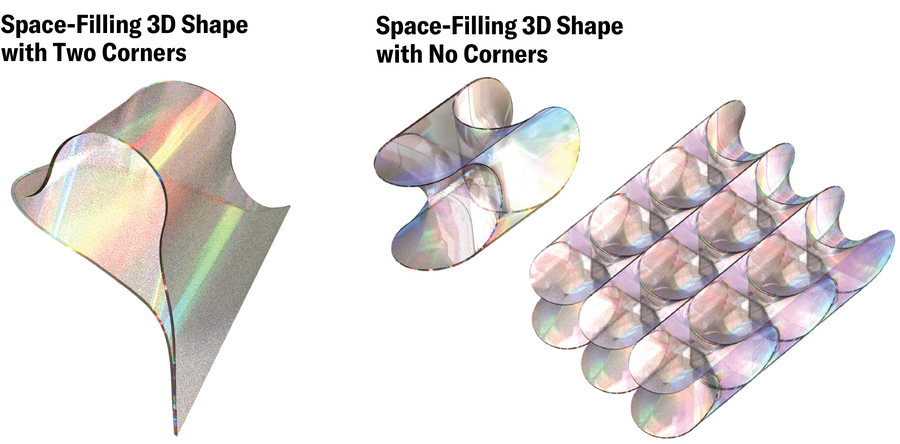
Violet Frances;资料来源:“软细胞和贝壳的几何形状”,作者:加博尔·多莫科斯、阿兰·戈里利、阿科斯·G·霍瓦特和克里斯蒂娜·雷戈斯;2024 年 2 月 6 日;arXiv:2402.04190(参考)
找到第一个软细胞解决了一个问题,并开启了无数个问题。例如,研究人员想知道是否可能存在只有一个角的空间填充形状。多莫科斯最终找到了一种。当他在黑板上为雷戈斯和霍瓦特画出草图时,他们“感到厌恶”,他说。这是一个丑陋的形状——一个没有对称性的变形形状,看起来像是外星人梦寐以求的东西。但在某种程度上,雷戈斯从这种丑陋中瞥见了可能性。“我有一天看到了它,然后意识到,”她说。“我们可以做这种边缘弯曲的事情,并创造柔软感。”
雷戈斯的直觉是,她可以通过弯曲普通尖角多面体的边缘来创建软细胞。在三个边缘相交的每个顶点处,她会抓住两个边缘,并将它们强制弯曲成平行于顶点之前剩余边缘的曲线。3D 空间中的封闭实体必须包围 4π 度的曲率,曲率通常集中在顶点处。雷戈斯正在将曲率涂抹在边缘上。“我花了几天几夜才相信她所做的事情并非完全是垃圾,”多莫科斯说。
雷戈斯在用数学语言描述她的弯曲边缘方法时遇到了困难。但随后她意识到,这个过程可以归结为图论中一个容易解决的二维问题。每个多面体都有一个对偶——另一个多面体,其面对应于其边,反之亦然。该团队表明,如果可以沿着多面体对偶的边缘找到一条恰好访问其每个顶点一次的路径(称为哈密顿回路),那么也可以将该形状变形为无角的空间填充软细胞。
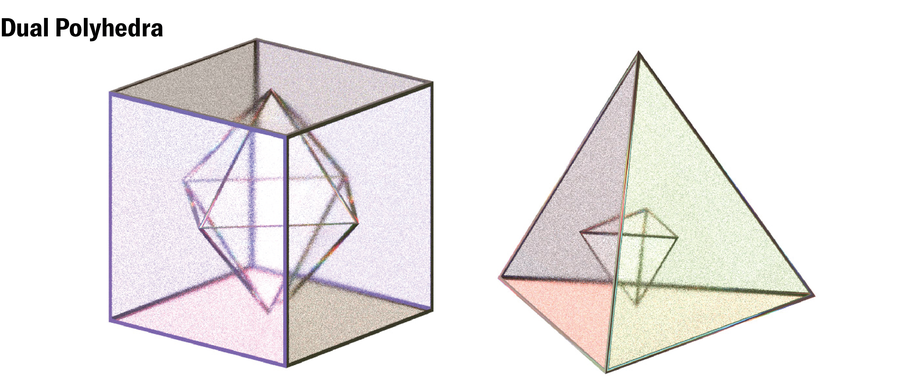
Violet Frances
有了这个条件,霍瓦特终于可以编写一个数学 3D 边缘弯曲算法。通过将无限类别的多面体平铺映射到软平铺,他证明了无限类别的软细胞的存在。换句话说,对于每个可以用自身填充空间的多面体(具有平面多边形面的 3D 形状),也必须存在弯曲的软细胞。
对于奥鲁尔克来说,边缘弯曲算法是论文中最美妙和最重要的部分。这种优雅来自于将两个完全不同的数学领域结合在一起。哈密顿回路纯粹是组合的(与计数的数学有关)——它们“与几何无关”,奥鲁尔克解释说。“但是在这里,你非常专注于几何。然而,你需要这个组合条件。所以我发现这非常好。”
Violet Frances;资料来源:“软细胞和贝壳的几何形状”,作者:加博尔·多莫科斯、阿兰·戈里利、阿科斯·G·霍瓦特和克里斯蒂娜·雷戈斯;2024 年 2 月 6 日;arXiv:2402.04190(参考)
当数学家们开始理解二维软细胞的数学原理时,他们开始意识到这些形状不仅仅存在于他们的草图和笔记中。“它们就在我们眼皮底下,”多莫科斯说。该团队开始在各处看到双顶点瓦片的平面马赛克,从肌肉组织到斑马条纹。有一次,在布达佩斯的一次散步中,雷戈斯甚至在金属安全格栅的弯曲交叉处看到了它们。
与此同时,三人组发现了越来越多的 3D 软细胞——雷戈斯在多莫科斯的第一个形状(变形的立方体)的基础上添加了四个平行多面体和四面体的变形版本。但是,研究人员很难在现实世界中识别出这些 3D 软细胞。这种情况在多莫科斯第一次发现边缘弯曲的立方体大约一年后发生了变化,他意识到他以前在某个地方见过它——不是在自然界中,而是在建筑中。
大约十年前,建筑师维基·桑多尔和维也纳大学的一群学生为太阳马戏团表演中心构思了一个 необычный 设计。这座建筑从未建成,但在建筑界引起了一些关注。它的基本构建模块是一个形状,看起来几乎与多莫科斯的立方软细胞完全相同。
桑多尔的项目最初是围绕“平衡”主题的热身练习,这位现任奥地利技术研究所的建筑师说。这座建筑必须是模块化的,因此他们将其划分为立方体模块,每个模块由不同的人设计。巧合的是,该设计的灵感来自一种名为 gömböc 的自平衡形状,该形状由多莫科斯和结构力学研究员彼得·瓦尔科尼在 2006 年发现。桑多尔和她的队友喜欢 gömböc 的细而肥的对比,并希望找到一种类似的形状,可以将不同的模块组合在一起。他们在网球的 C 形曲线中找到了答案。“如果你沿着 C 形切割,那么你会得到一个非常薄和一个非常肥的元素。而 gömböc 遵循了这个原则,”桑多尔说。事实证明,将弯曲表面切割成管状或棱柱状是构建软细胞的好方法——不仅在理论或设计中,而且在自然界中也是如此。
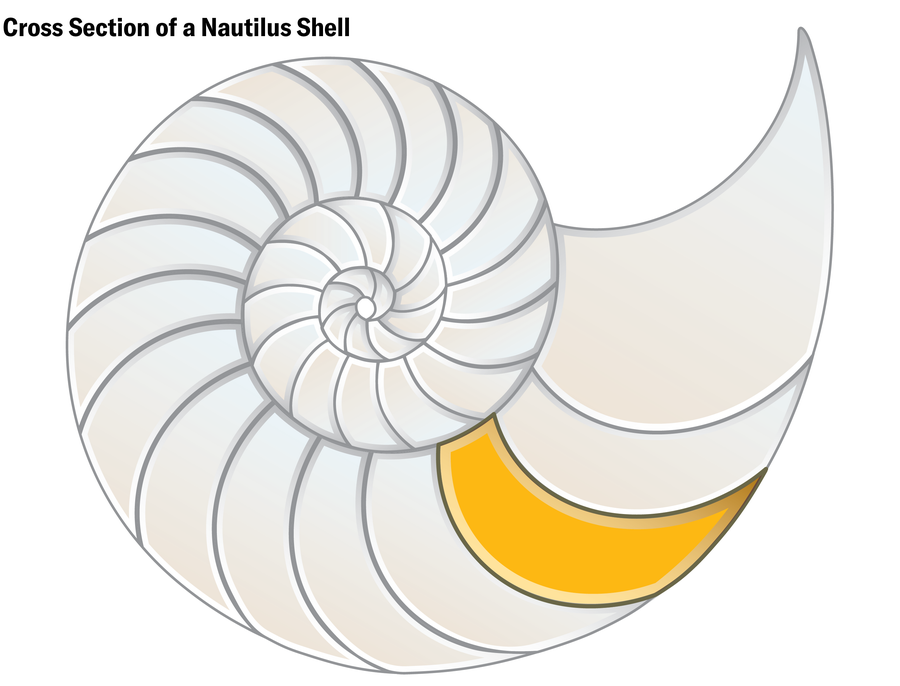
雷戈斯凭直觉发现了第一个天然 3D 软细胞。有一天,她突然给多莫科斯发了一张鹦鹉螺壳横截面的照片。多莫科斯回复说,这是一个二维软细胞的很好的例子。雷戈斯回复说:不,它们是 3D 软细胞。“它看起来一点都不软,”多莫科斯心想。“我的意思是,它有角。” 但雷戈斯坚持己见。因此,多莫科斯买了两个鹦鹉螺壳,并将它们交给雷戈斯和霍瓦特进行检查。他们玩弄贝壳大约 30 分钟后放弃了。多莫科斯说,即使他们可以通过观察贝壳来说服自己,“你也不能将贝壳作为附件发送给论文。”
Jen Christiansen;资料来源:“软细胞和贝壳的几何形状”,作者:加博尔·多莫科斯、阿兰·戈里利、阿科斯·G·霍瓦特和克里斯蒂娜·雷戈斯;2024 年 2 月 6 日;arXiv:2402.04190(参考)
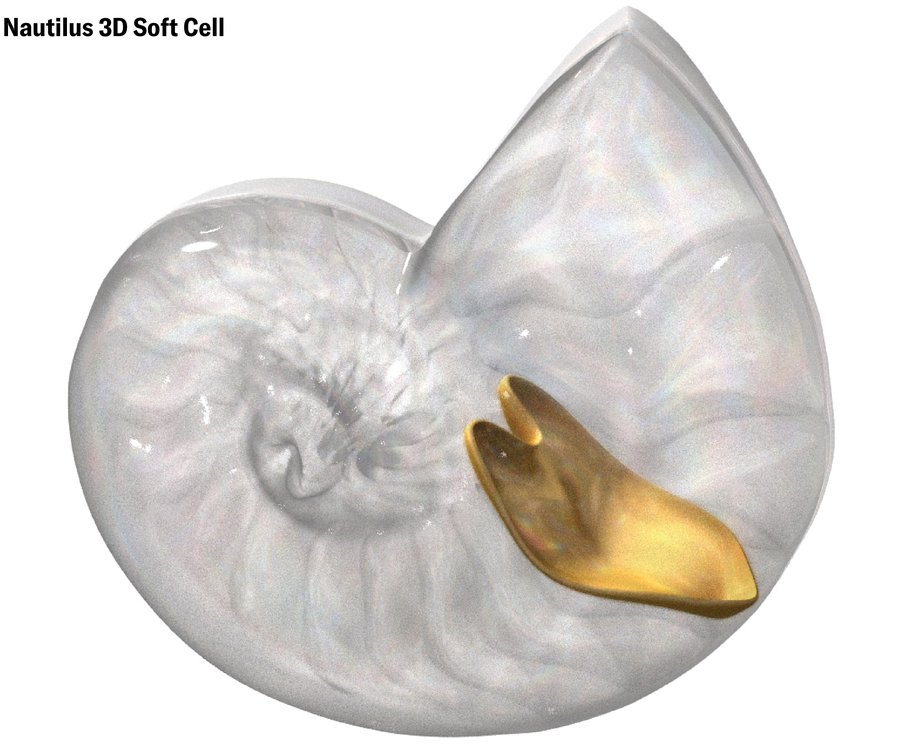
如果不是苏格兰邓迪大学的达西·汤普森动物学博物馆发布了一组免费提供的微型 CT 扫描,这个想法可能就此作罢。多莫科斯在网上找到了扫描结果,并花费数小时“在贝壳内部爬行”,寻找角。他找不到任何角。
Violet Frances;资料来源:“软细胞和贝壳的几何形状”,作者:加博尔·多莫科斯、阿兰·戈里利、阿科斯·G·霍瓦特和克里斯蒂娜·雷戈斯;2024 年 2 月 6 日;arXiv:2402.04190(参考)
团队中没有人对贝壳一窍不通。但多莫科斯认识一个懂行的人:阿兰·戈里利,牛津大学的物理学家和应用数学家,他研究过有腔室的贝壳。多莫科斯很紧张地告诉小组外的人这个项目,尤其是现在他们已经在鹦鹉螺壳内发现了软细胞——鹦鹉螺壳是喜欢自然形状的数学家最喜欢的形状。很容易抢先他们的想法并先发表。但多莫科斯认识戈里利几十年了,所以他决定冒险给他打电话。不久之后,他和雷戈斯登上了一架飞往牛津的飞机。
戈里利立即被鹦鹉螺壳内软细胞的发现所吸引。“我发现自然界中的形状以这种方式发展是很自然的,因为形成尖角代价很高,”戈里利说。生物细胞是柔软的,表面张力自然会使它们变圆,除非生物体消耗能量来构建可以保持更尖形状的刚性结构。而且,生物体内的细胞希望以少量间隙有效地填充空间。
在他们在牛津疯狂的三天以及随后的几个月中,戈里利和匈牙利人发现了越来越多的自然和艺术界的软细胞例子。斑马条纹、河流入海口、洋葱横截面、贝壳、麦穗、红细胞、植物和真菌都类似于二维软细胞。在建筑方面,二维软细胞为建筑师扎哈·哈迪德的许多建筑物赋予了未来主义的有机形式。它们也出现在日本艺术家葛饰北斋的榻榻米和服装草图中,葛饰北斋创作了著名的 1831 年画作《神奈川冲浪里》,以及光学艺术运动的“祖父”维克多·瓦萨雷里的艺术作品中。
戈里利还帮助该团队找到了另一个 3D 软细胞的例子:菊石壳的腔室。然后,雷戈斯设计了一个几何模型,该模型从第一性原理产生了类似于贝壳示例的形状。像鹦鹉螺壳中的软细胞那样,通过将棱柱与弯曲表面相交,可以轻松地制造出软细胞——这与桑多尔和她的团队用于设计太阳马戏团建筑的过程相呼应。“令人高兴的是,建筑师也凭直觉达到了 [这个过程],”戈里利说。“根据我们的理解,他们是出于同样类型的要求而达到这个目标的:他们想软化结构。”
古德曼-施特劳斯说,这项工作建立了一个探索软形状的“有用词汇”——这个词汇开启了新的数学问题。存在哪些类别的软单瓦片?哪些软形状组可以和不可以平铺空间?多莫科斯想知道柔软度与非周期性(在不创建重复图案的情况下平铺平面的能力)有何关系。去年,第一个非周期性单瓦片(用自身副本填充空间但从不重复图案的单个形状)的发现成为头条新闻。多莫科斯和雷戈斯很好奇如果他们将边缘软化算法应用于 “幽灵”平铺(第一个真正的非周期性单瓦片)会发生什么。但他们惊讶地发现,其软化版本无法单独平铺平面。

Jen Christiansen;资料来源:“手性非周期性单瓦片”,作者:大卫·史密斯、约瑟夫·塞缪尔·迈尔斯、克雷格·S·卡普兰和海姆·古德曼-施特劳斯;2023 年 5 月 28 日;arXiv:2305.17743(参考)
阿肯色大学的古德曼-施特劳斯和安大略省滑铁卢大学的克雷格·S·卡普兰(他们都为第一个非周期性单瓦片的发现做出了贡献)一点也不感到惊讶。卡普兰说,数学家们才刚刚开始探索非周期性单瓦片,还有许多问题有待解答。
尽管软细胞在自然界中似乎无处不在,但这些形状的数学与生物学之间的联系目前只是一种视觉观察。多莫科斯承认这是这项工作的一个弱点,并希望确定它们在自然界中如此普遍的原因。“论文的很大一部分是关于视觉相似性,这非常不寻常,”他说。卡普兰说,进一步探索这种联系似乎很有希望。“我确实喜欢这种动机:只是简单地声称自然不喜欢尖锐的特征,所以让我们从数学的角度来研究它。这是一个很好的开场白,你可以从中发展出丰富的理论。”
古德曼-施特劳斯说,软细胞的概念最终可能会被证明是有用的——“不一定是今天的生物学家,而是 30 年后的生物学家”。也许软细胞的数学最终将捕捉到一些关于软物质的真实信息——软物质构成了我们世界的大部分,从我们血管中的血液到你现在可能正在阅读的液晶显示器。
关于软几何的问题特别棘手,因为它们往往会跨越学科界限。多莫科斯挣扎了几个月才找到一家愿意发表该团队“古怪”手稿的期刊,该手稿混合了数学、艺术和生物学。古德曼-施特劳斯对此并不感到惊讶。当被问及他认为软细胞在科学领域中属于哪里时,他不假思索地说。“我认为,”他说,“唯一的答案是它属于未来。”
