编者注:本文发表于 1957 年,摘自马丁·加德纳的传奇《大众科学》专栏“数学游戏”。在我们的特别数字期刊《趣味游戏》中阅读更多内容。
正如本杂志的许多读者所知,莫比乌斯带是一种几何奇观,它只有一个面和一个边缘。这种图形是称为拓扑学的数学分支所关注的。对数学有粗浅兴趣的人可能会认为,拓扑学家是一个数学花花公子,他把时间花在制作莫比乌斯带和其他有趣的拓扑模型上。如果他们打开任何最近的拓扑学教科书,他们会感到惊讶。他们会发现一页又一页的符号,很少有图片或图表来缓解这种枯燥。诚然,拓扑学起源于对几何谜题的思考,但今天它已成为抽象理论的丛林。拓扑学家怀疑那些必须通过可视化才能理解的定理。
尽管如此,严肃的拓扑学研究仍然不断产生怪异而有趣的模型。例如,考虑一下双莫比乌斯带。它是通过将两条纸条放在一起形成的,像一条纸条一样给它们一个半扭,并将它们的末端连接起来,如下面的插图所示。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
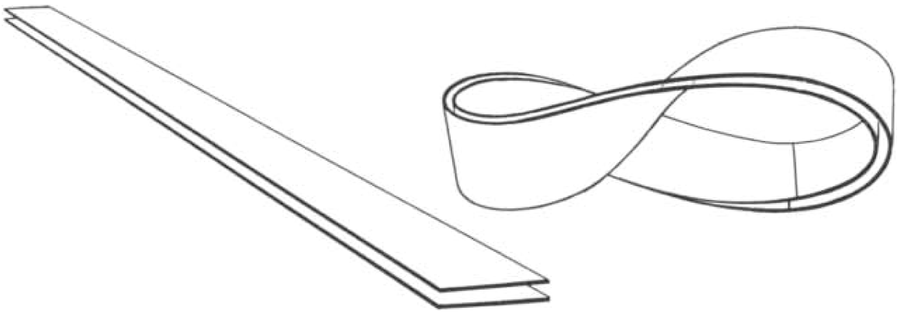
双莫比乌斯带是通过将两条纸条放在一起(左),给它们都扭转半圈,然后按照右侧直线指示的方式连接起来制成的。
詹姆斯·埃格尔森
我们现在拥有看起来像是两个嵌套的莫比乌斯带。事实上,您可以通过将手指放在带子之间并绕着它们一直移动,直到回到您开始的点来“证明”有两个独立的带子。一只在带子之间爬行的虫子可以无限期地绕着它们转圈,始终在一个带子上行走,而另一个带子沿着它的背部滑动。它永远不会发现“地板”与“天花板”相遇。一只聪明的虫子会得出结论,它正在两条独立带子的表面之间行走。
然而,假设这只虫子在地板上做了一个标记,并绕着带子转圈直到再次到达标记。它会发现标记不在地板上,而是在天花板上,并且需要第二次绕着带子转圈才能在地板上找到它!这只虫子需要相当的想象力才能理解地板和天花板都是同一条带子的一个面。看起来像是两条嵌套的带子实际上是一条大的带子!当您将模型展开成大的带子时,您会发现很难将其恢复到原来的形状。
当带子呈双重形式时,它的两个独立的边缘彼此平行运行;它们绕着模型转两圈。想象一下,这些边缘被连接起来,并且带子是由薄橡胶制成的。那么您将得到一个管子,可以充气使其成为环面(拓扑学家对甜甜圈表面的术语)。连接的边缘将形成一条围绕环面盘绕两圈的闭合曲线。这意味着可以沿着这样一条曲线切割环面,从而形成双莫比乌斯带。
事实上,双带与一条在末端连接之前被给予四个半扭的单带相同。可以将环面切割成具有任何期望的偶数个半扭的带子,但不可能切割它以产生具有奇数个这种扭转的带子。这是因为环面是一个双面表面,只有具有偶数个半扭的带子才是双面的。虽然双面表面可以通过切割单面表面来制成,但反之则不可能。如果我们希望通过切割没有边缘的表面来获得单面带(具有奇数个半扭的带子),我们必须求助于切割克莱因瓶。艾尔伯特·W·塔克和赫伯特·S·贝利在《拓扑学》中描述了这个非凡的单面瓶。[大众科学; 1950 年 1 月]。
简单的莫比乌斯带是通过在连接末端之前给纸条扭转半圈制成的。能否以某种方式拉伸带子,直到这个边缘变成三角形?答案是肯定的。第一个设计出这种模型的人是布莱恩特·塔克曼,他是折叠弹性多面体艺术的四位先驱之一 [“数学游戏”;1956 年 12 月]。下面的插图展示了如何切割、折叠和粘贴一张纸来创建塔克曼的模型。
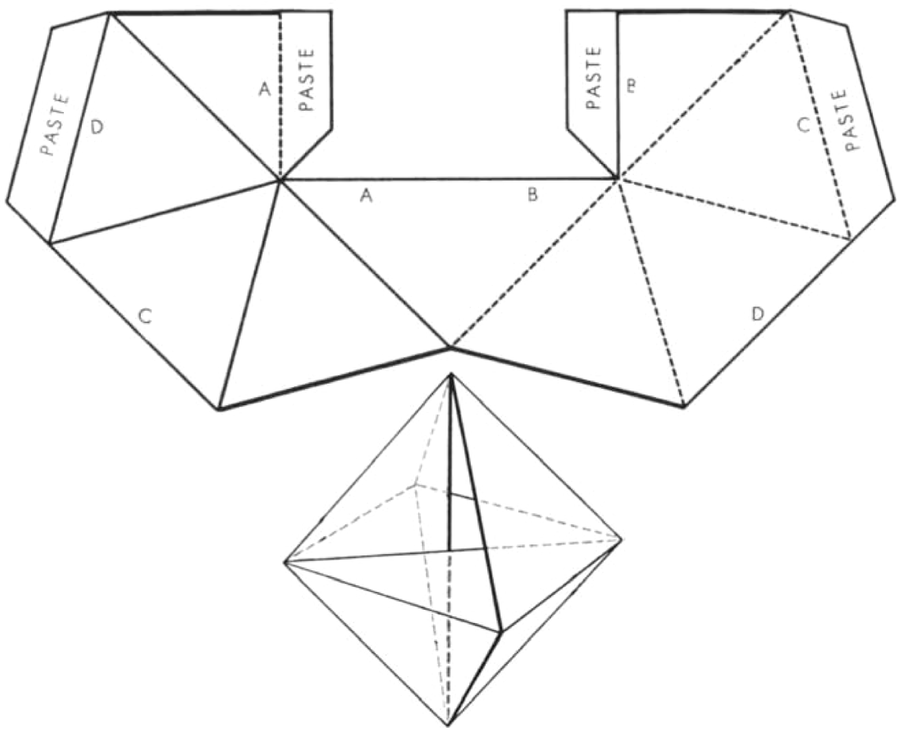
带有三角形边缘的莫比乌斯带是由布莱恩特·塔克曼设计的。如果将平面图形重新绘制,最好按比例放大,则可以按如下方式组装尺寸多面体模型。首先,剪下图形。其次,沿着实线“向下”折叠。第三,沿着虚线向相反方向折叠。第四,通过将胶水涂在四个标签上,连接边缘 A 和 A、B 和 B、C 和 C 以及 D 和 D。完成的多面体中的粗线描绘了莫比乌斯曲面的三角形边界。
詹姆斯·埃格尔森
表面不仅可以有一个或两个面;它们的拓扑结构也可能因边缘的数量和结构而异。这些特征不能通过扭曲表面来改变;因此,它们被称为拓扑不变量。让我们考虑边缘不超过两个的表面,以及边缘是简单的闭合曲线或普通单结形式的表面。如果表面有两个边缘,它们可以是彼此独立的或链接的。在这些限制范围内,我们可以列出以下 16 种表面(不包括无边缘表面,如球体、环面和克莱因瓶):
单面,单边缘
1. 边缘是简单的闭合曲线。
2. 边缘是打结的。
双面,单边缘
3. 边缘是简单的闭合曲线。
4. 边缘是打结的。
单面,双边缘
5. 两个边缘都是简单的闭合曲线,未链接。
6. 两个边缘都是简单的闭合曲线,已链接。
7. 两个边缘都是打结的,未链接。
8. 两个边缘都是打结的,已链接。
9. 一个边缘是简单的;一个是打结的,未链接。
10. 一个边缘是简单的;一个是打结的,已链接。
双面,双边缘
11. 两个边缘都是简单的闭合曲线,未链接。
12. 两个边缘都是简单的闭合曲线,已链接。
13. 两个边缘都是打结的,未链接。
14. 两个边缘都是打结的,已链接。
15. 一个边缘是简单的;一个是打结的,未链接。
16. 一个边缘是简单的;一个是打结的,已链接。
纸模型很容易构建,以说明这 16 种表面中的每一种的示例。下面描绘了表面 1 到 12 的模型。读者可能会喜欢尝试构建剩余四个表面的模型,其图纸将在下个月的专栏中出现。
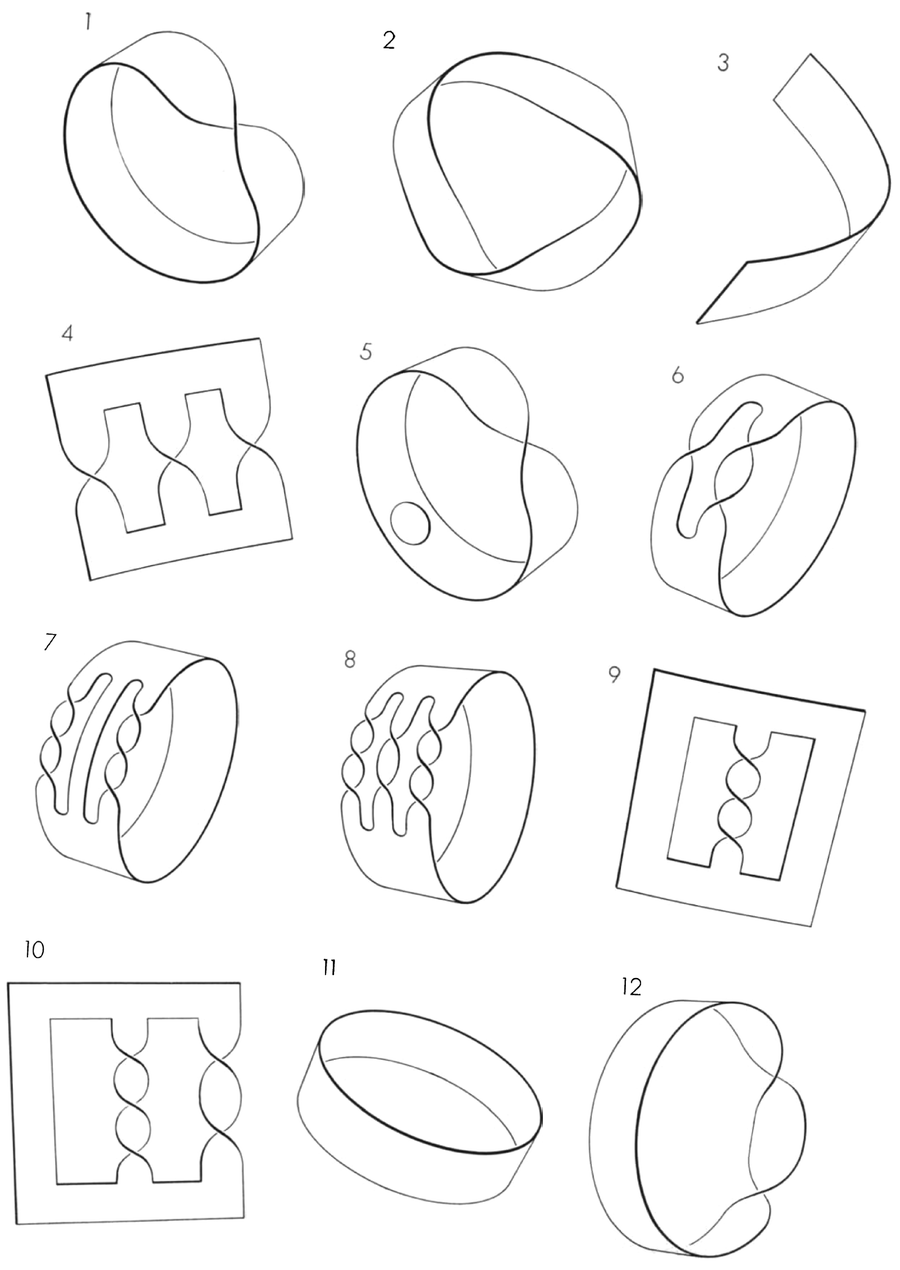
拓扑模型是 16 个模型中的 12 个,这些模型可以用边缘不超过两个的表面以及简单闭合曲线或单结的边缘制成。简单的莫比乌斯带是 1。
詹姆斯·埃格尔森
当用剪刀以某种方式切割其中一些模型时,结果令人震惊。正如几乎所有玩过莫比乌斯带的人都知道的那样,纵向将带子对半切割并不会像人们可能预期的那样产生两条独立的带子,而是一条大的带子。(这条大的带子有四个半扭;因此它可以制成前面描述的双莫比乌斯带。)不太为人所知的是,如果您从一个边缘和另一个边缘之间三分之一的位置开始切割,并一直切割到回到起点,则莫比乌斯带会展开成一条大的带子,并与一条小的带子链接在一起。
将表面 12 对半切割会产生两条相同大小的互锁带子,每条都与原始带子完全相同。将表面 2 对半切割会产生一条大的带子,带子上有一个结。后一种特技是一本小册子的主题,该小册子在 1880 年代在维也纳广为销售。这本小册子揭示了在布带上打结而无需借助魔术的秘密。
在说两个边缘“链接”时,我们指的是像链条中两个链环一样链接的方式。要分离这些链接,必须打开一个链环并将另一个链环穿过开口。然而,有可能以这样一种方式将两条闭合曲线互锁,以至于为了分离它们,不需要将一条穿过另一条的开口。最简单的方法如下面的插图中的上部曲线所示。这些曲线可以通过在 A 点将黑色曲线穿过自身来分离。

互锁的曲线可以分离,而无需将一条穿过另一条的开口。顶部的曲线可以通过在 A 点将黑色曲线穿过自身来分离。
詹姆斯·埃格尔森
插图底部的三条闭合曲线也是不可分离的,但没有链接。如果您移除任何一条曲线,其他两条曲线是自由的;如果您链接任何一对曲线,它会释放第三条曲线。顺便说一句,这种结构在拓扑学上与著名啤酒品牌的熟悉的三环商标相同。这些被称为博罗梅安环,因为它们构成了文艺复兴时期意大利博罗梅奥家族的纹章。
