2024年10月12日

数学谜题：用纸牌屋玩建筑师

作者：汉斯-卡尔·埃德尔

乔万用总共 90 张扑克牌搭建了这五座纸牌屋。现在他想用正好 100 张牌搭建一座大型纸牌屋。这样的纸牌屋存在吗？

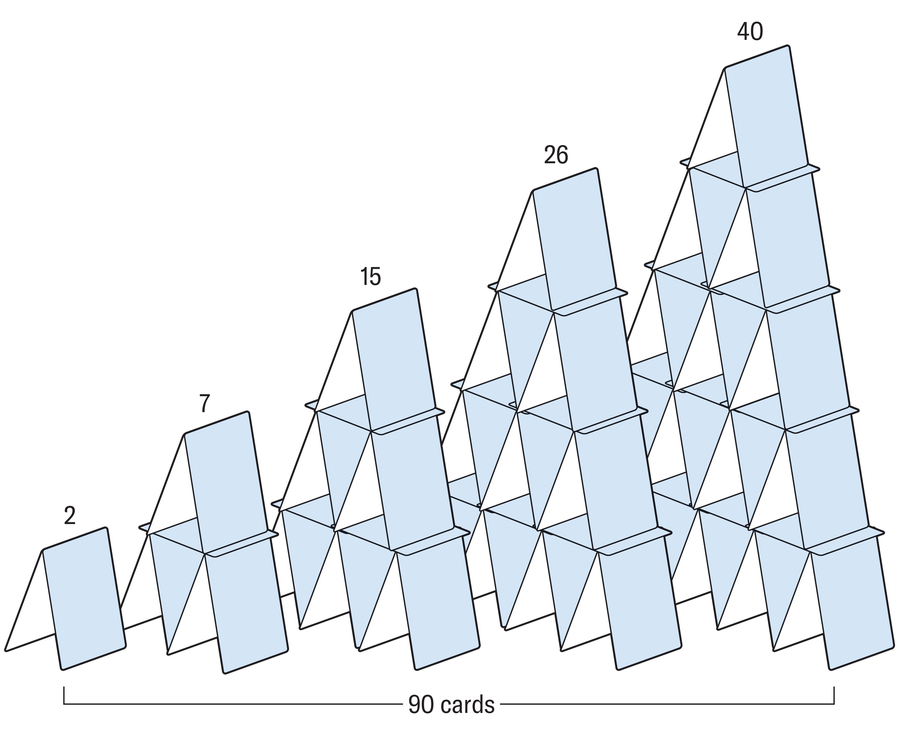
Graphic shows five triangle-shaped houses of cards composed of the following numbers of cards: 2, 7, 15, 26 and 40. The total number of cards shown is 90.

阿曼达·蒙塔涅斯；来源：汉斯-卡尔·埃德尔/《科学光谱》(参考文献)

你可以用正好 100 张牌搭建一座纸牌屋；它将有八层。

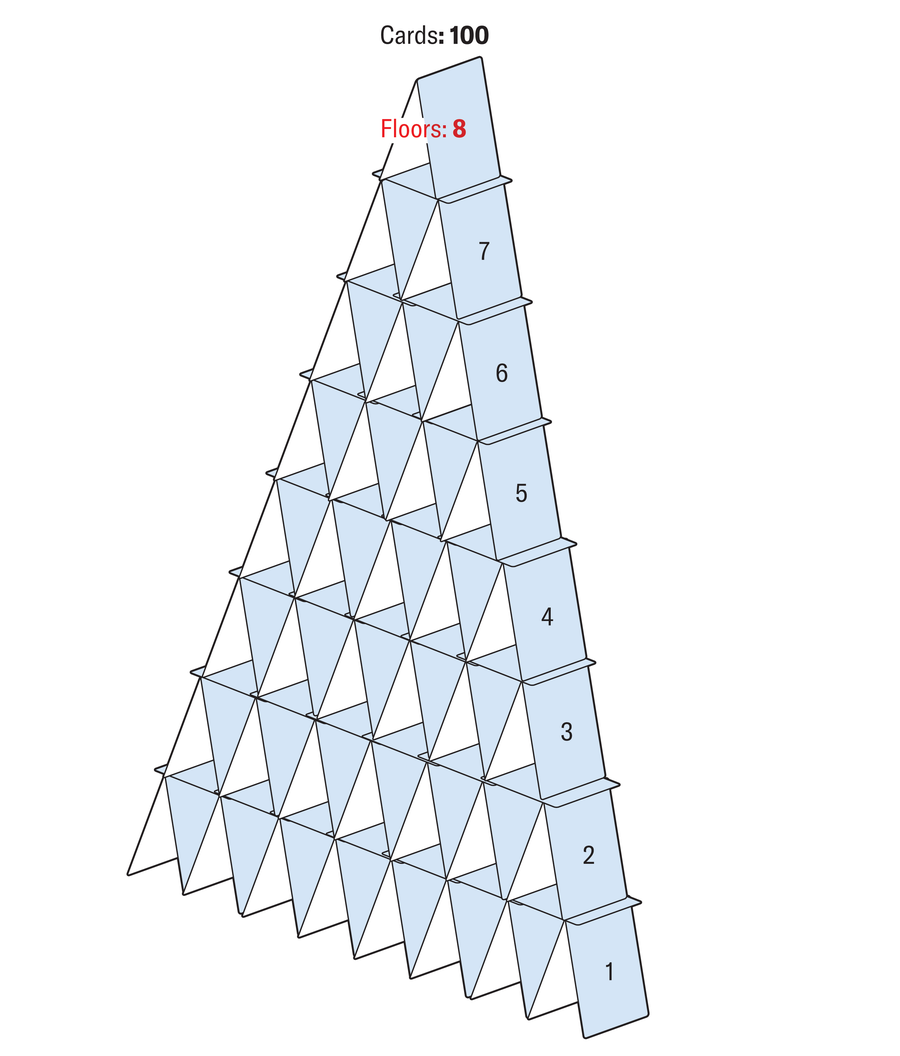
Graphic shows a triangle-shaped house of cards that has eight floors and is composed of 100 cards.

阿曼达·蒙塔涅斯；来源：汉斯-卡尔·埃德尔/《科学光谱》(参考文献)

纸牌的数量逐层以恒定序列增加。如果你想证明谜题的答案，你必须证明 100 是这个序列中的一项。

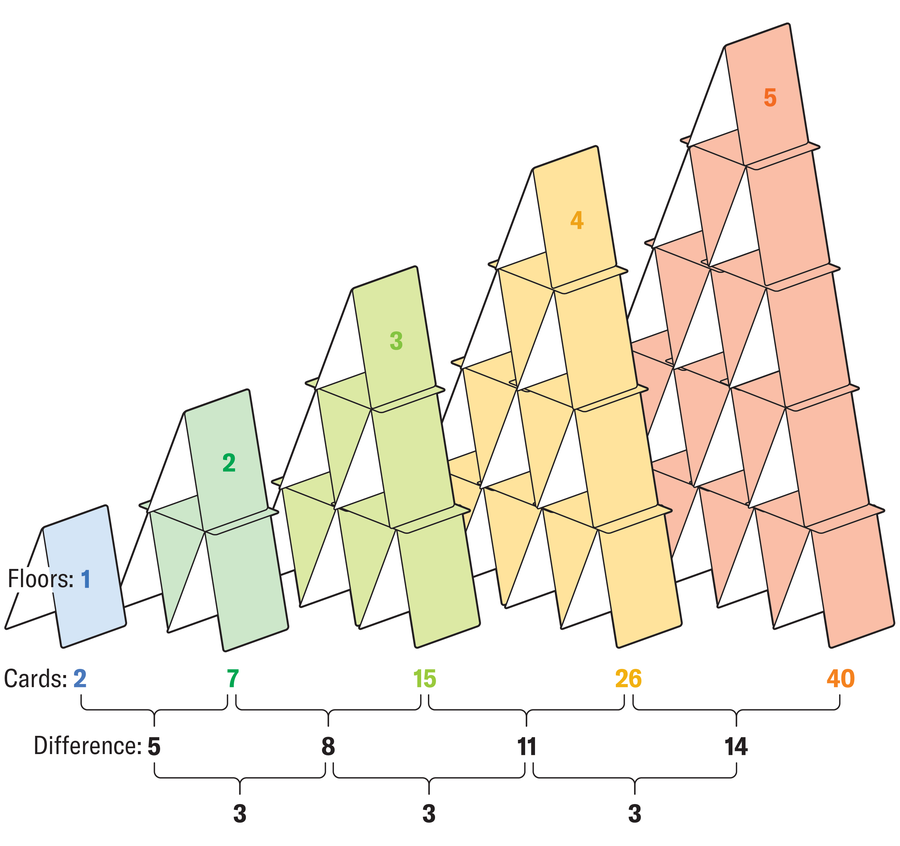
Graphic shows five triangle-shaped houses of cards composed of 2, 7, 15, 26 and 40 cards. The number of floors in each house is highlighted: 1, 2, 3, 4 and 5. The increase in the number of cards at each step is shown (7 minus 2, 15 minus 7, and so on), followed by the difference between each of those increases (8 minus 5, 11 minus 8, and so on), which equals 3.

阿曼达·蒙塔涅斯；来源：汉斯-卡尔·埃德尔/《科学光谱》(参考文献)

这是一种方法。因为项之间的差值始终变化相同的量——“二阶差分”是恒定的——你可以得出结论，纸牌数量 K 和层数 x 的序列可以用 K = ax2 + bx + c 形式的二次方程表示。

首先，确定 a、b 和 c 的值。这可以使用三个方程组来实现

A system of three equations is created from the first three terms in the house of cards sequence: 2 equals a times 1 squared plus b times 1 plus c; 7equals a times 2 squared plus b times 2 plus c; 15 equals a times 3 squared plus b times 3 plus c. Subtracting the first equation from the second one gives an equation designated capital A: 5 equals 3a + b. And subtracting the second equation from the third one gives an equation designated capital B: 8 equals 5a plus b. Subtracting equation capital A from equation capital B allows you to calculate that a equals 1.5. And inserting that into equation capital B lets you find that b equals 0.5. Combining those values for a and b with your original first equation, 2 equals a plus b plus c, reveals that c equals 0.

阿曼达·蒙塔涅斯；来源：汉斯-卡尔·埃德尔/《科学光谱》(参考文献)

有了 a、b 和 c 的值以及计算出的 K = 100 值，你现在可以解二次方程。

Graphic 5 alt text: Now you can insert the number of cards K equals 100 into the quadratic equation K equals a times x squared plus b times x plus c. Using the values you found earlier, you get the equation 100 equals 1.5 times x squared plus 0.5 times x plus 0. Divide both sides by 1.5 and move all terms to one side to find x squared plus one third times x minus 200 thirds equals 0, which is equivalent to x minus 8 times x plus 25 thirds equals 0. Therefore, x equals 8 or negative 25 thirds.

阿曼达·蒙塔涅斯；来源：汉斯-卡尔·埃德尔/《科学光谱》(参考文献)

x 的值之一是自然数，它让你可以用正好 100 张牌搭建一座纸牌屋。

我们很乐意听到你的来信！请发送电子邮件至 games@sciam.com 分享你的体验。

这个谜题最初出现在《科学光谱》中，经许可转载。

0
© . All rights reserved.