核心概念
数学
加法
计数
谜题
引言
你是否曾经使用数学作为工具来解决有趣的问题?在 20 世纪 70 年代,数学通常是通过简单的练习册来教授的。一位老师正在寻找一种方法来帮助他的学生在数学和逻辑中获得更多乐趣。因此,他开发了现在被称为周长幻方三角形谜题的东西。尝试一下——并开始以全新的方式思考计数,享受一些乐趣!
背景
计数是如此普遍,以至于我们忘记了它与更广泛的数字研究领域(称为算术)的联系。我们可以将计数视为重复加一:当你将一个物体添加到另一个物体时,你有两个物体。再加一个,你就有了三个,以此类推。加法是加数字的过程。加法的结果称为和。对于较小的数字,你可能会使用计数来找到和。例如,当你得到三,想加上二时,你可以从三开始数两个数字,得到五。经过大量的练习,你通常可以记住 1 到 10 的数字之和——此时,玩数字,找到构成特定和的所有方法会很有趣。
关于支持科学新闻
如果你喜欢这篇文章,请考虑订阅以支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,你正在帮助确保关于塑造我们当今世界的发现和想法的具有影响力的故事的未来。
数学谜题和游戏可以是一种练习使用数字的有趣方式。谜题还提供了有趣的途径来培养战略性和逻辑性思维。通过一些试错,你通常可以开始找到新的策略来更快地完成谜题。这些正是数学家使用的技术:从小处着手,并尝试在答案序列中找到模式。然后,这些模式用于预测更大谜题的答案。
如果这一切都太抽象,请尝试此活动中提供的谜题!它可能会使学习算术的过程变得清晰。
材料
两张 9 英寸 x 12 英寸的纸,例如结构纸或工艺纸(如果可能,请选择对比色)
铅笔或记号笔
尺子
剪刀
四分之一硬币或其他类似大小的圆形物体
21 个硬币、小方块或其他小型可堆叠物体
更多纸张(可选)
准备工作
在纸上画一个大三角形(你可以使用尺子来帮助画直线)。
在三角形的每个角上用四分之一硬币描出一个圆。现在在三角形的每条边的中间描出一个圆。你应该有六个圆。
在第二张纸的底部画六个大小与三角形上绘制的圆相似的圆。
剪下这些圆,并将其编号为 1 到 6。这些圆将被称为数字盘。
保留第二张纸的顶部。你将用它来写下你的结果。
步骤
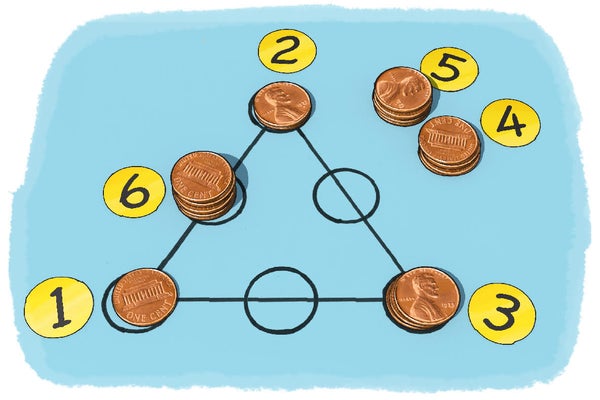
在画有三角形的纸上,使用 21 个硬币在每个圆上建造塔。每个圆必须至少有 1 个硬币,但没有两个塔的高度相同。你能做到吗?
不断尝试,直到找到解决方案!
数数每个塔中的硬币数量。按从小到大的顺序写下每个总和。你对这组数字有什么看法?
移动塔或重建塔,直到你能满足另一个要求:用于在三角形的每一边上建造三个塔的硬币总数必须相同。例如,如果在三角形的一侧排列的圆中建造 1、5 和 3 个硬币的塔,则在该侧使用了 1 + 5 + 3 = 9 个硬币。在相邻侧排列 1、2 和 4 个硬币的塔将不起作用,因为 1+ 2 + 4 = 7——不像第一侧那样是 9。(请注意,1 个硬币的塔位于此三角形的角上,因此它对两条边都有贡献。)如果你尝试用 1、2 和 6 作为相邻侧,那将起作用,因为 1 + 2 + 6 = 9。现在你可以放置剩下的一个塔,并检查此三角形的第三侧的三个塔中是否使用了 9 个硬币。尝试一下!你找到解决方案了吗?
如果这不是一个解决方案,请思考。你能重新排列几个塔并得到一个解决方案吗?
如果使用抽象数字对你来说更容易,请用数字盘替换塔。然后,每个数字盘代表一个硬币塔。数字盘上写的数字会告知你该塔中的硬币数量。
每边使用 9 个硬币是可能的!你找到解决方案了吗?是否可以通过几种方式排列塔,使每边都使用 9 个硬币?
你能否排列硬币,使每边使用 10 个、11 个甚至 12 个硬币?
附加题:证明没有每边使用 8 个或更少硬币的解决方案,或者证明没有每边总共使用 13 个或更多硬币的解决方案。
附加题:此活动中提出的谜题称为“三阶周长幻方三角形”。要将其扩展到更高阶的周长幻方三角形,首先画一个新的三角形。像第一次一样在角落上添加圆,但这次在角落之间的每一侧添加两个圆。对于这个谜题,你将需要九个数字盘。将其编号为 1 到 9。就像在之前的谜题中一样,你需要找到将数字盘放在圆上的方法,以便此三角形每侧的数字之和都相同。数学家称此三角形为四阶三角形,因为它每侧有四个数字。解决此谜题后,继续使用五阶三角形(在角落之间添加三个圆并剪下 12 个数字盘),然后使用六阶三角形,以此类推。
附加题:你能否创建一种策略来快速找到此类谜题的解决方案?
观察和结果
你是否发现,如果需要制作六个高度不同的塔,你只能将 21 个硬币排列成 1、2、3、4、5 和 6 个硬币的塔?你是否能想出排列塔的方法,使三角形每边使用的硬币之和对于所有三边都相同?每边总共可以使用 9、10、11 和 12 个硬币。
为了在每边使用总共 9 个硬币,你将 1、2 和 3 个硬币的塔放在三角形的角上。6 个硬币的塔放在 1 和 2 个硬币的塔之间,因为 1 + 2 + 6 = 9。5 个硬币的塔位于 1 个硬币的塔和 3 个硬币的塔之间,因为 1 + 3 + 5 也等于 9。2、4 和 3 个硬币的塔填满了第三行。请注意,对于此解决方案,最小的塔放在角落里。
要排列塔,使每边使用 12 个硬币,首先在三角形的角上排列最高的塔(那些有 6、5 和 4 个硬币的塔),并在中间的圆中填充。将你剩下的最小的塔(高 1 个硬币)放在两个最高的塔(每个 5 和 6 个硬币)之间。你是否看到剩下的最小的塔(高 2 个硬币)位于需要中间塔的最高的塔之间(每个塔有 6 和 4 个硬币)?
你可以用来找到每边都有 10 个硬币的解决方案的策略是列出所有可以通过添加三个不同数字得到 10 的方法。你会发现 3 + 2 + 5 = 10、5 + 4 + 1 = 10 和 1 + 6 + 3 = 10。你能看到 3、5 和 1 是这些总和中的两个的一部分吗?这意味着这些位于三角形的角上。你可以使用相同的策略来找出如何放置硬币,以便每边使用 11 或 12 个硬币。
你是否想知道你怎么知道每边使用 8 个硬币是不可能的?每边使用 8 个硬币,你将在三角形上使用 3 X 8,即 24 个硬币。因为你重复使用角塔上的硬币,所以你最多使用 1 + 2 + 3(三个最小塔的总和)或少用 6 个硬币。换句话说,你最多可以使用 18 个硬币。该谜题要求你使用 21 个硬币。
更多探索 来自幻方网的周长幻方三角形
《汉诺塔》,来自《大众科学》 统计科学:入口即化的数学,来自《大众科学》 儿童 STEM 活动,来自科学伙伴
此活动由 科学伙伴 合作提供