大型强子对撞机(LHC)是人类有史以来建造的最大机器。它汇集了100多个国家的资源,将质子加速到接近光速百万分之一的速度。当它们碰撞时,质子会分解成其组成部分(夸克和将它们粘合在一起的胶子粒子),并产生以前不存在的粒子。2012年,LHC就是通过这种方式首次探测到希格斯玻色子,这是粒子物理学标准模型预测的最后一个缺失粒子。现在物理学家们希望LHC能发现真正的新事物:他们现有理论中尚未包含的粒子——例如,解释暗物质之谜或为其他长期存在的问题提供解决方案的粒子。为了实现这样的发现,科学家们必须仔细研究该机器每年产生的30拍字节数据,以识别结果与标准模型略有不符的微小偏差。
当然,如果我们不知道标准模型预测什么,所有这些努力都将是徒劳的。
这就是我的工作所在。我们想提出的关于LHC的问题以概率的形式出现。“两个质子相互反弹的几率是多少?”“我们多久会产生一个希格斯玻色子?”科学家们用“散射振幅”来计算这些概率,散射振幅是一些公式,告诉我们粒子以特定方式“散射”(本质上是反弹)的概率有多大。我是一个物理学家和数学家小组的成员,我们致力于加速这些计算,并找到比我们科学前辈遗留下来的旧的、笨拙的方法更好的技巧。我们称自己为“振幅学家”。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
振幅学家将我们的领域追溯到两位物理学家斯蒂芬·帕克和托马兹·泰勒的研究。1986年,他们发现了一个单一公式,描述了任意数量的胶子之间的碰撞,简化了通常需要数页纸仔细逐案计算的内容。这个领域实际上是在1990年代和2000年代初期开始兴起的,当时大量新方法有望简化各种粒子物理计算。如今,振幅学蓬勃发展:“2018年振幅”会议有160名参与者,前一周的暑期学校有100人参加,旨在培训年轻研究人员掌握该领域的技巧。我们也获得了一些公众的关注:物理学家尼玛·阿卡尼-哈米德和雅罗斯拉夫·特恩卡的振幅体(一种用几何语言描述某些振幅的方法)在2013年登上了新闻,在电视节目《生活大爆炸》中,谢尔顿·库珀也以涉猎振幅学而闻名。
最近,我们向前迈进了一大步,从我们已经开发的基本工具转向更复杂的技术。我们正在进入一个计算领域,其灵敏度足以匹配LHC日益提高的精度。借助这些新工具,我们准备好检测标准模型预测与LHC内部现实之间哪怕是微小的差异,从而有可能最终揭示物理学家梦寐以求的未被发现的粒子。
圈和线
为了组织我们的计算,科学家们长期以来一直使用名为费曼图的图片。这些图由物理学家理查德·费曼于1948年发明,描绘了粒子行进的路径。假设我们想知道两个胶子合并形成希格斯玻色子的几率。我们首先绘制代表我们已知粒子的线条:两个入射胶子和一个出射希格斯玻色子。然后,我们必须根据标准模型的规则,通过在图的中间绘制更多的粒子线来连接这些线。这些额外的粒子可能是“虚粒子”:也就是说,它们并非字面意义上的粒子,就像我们图中的胶子和希格斯玻色子那样。相反,它们是一种简写,一种跟踪不同量子场如何相互作用的方式。
费曼图不仅仅是漂亮的图片——它们是指令,告诉我们使用关于我们绘制的粒子的信息来计算概率。如果我们知道图中的胶子和希格斯玻色子的速度和能量,我们可以尝试计算出中间虚粒子的性质。然而,有时答案是不确定的。沿着粒子路径追踪你的手指,你可能会发现一个闭环:一条最终回到你起点的路径。像那样在环路中行进的粒子不是“输入”或“输出”:它的性质永远不会被测量。我们不知道它的速度有多快或能量有多大。尽管这违反直觉,但这是量子力学基本不确定性的结果,量子力学阻止我们同时测量粒子的两个特征,例如速度和位置。量子力学告诉我们如何处理这种不确定性——我们必须将每种可能性相加,将虚粒子可能具有的任何速度和能量的概率相加,使用一种你可能还记得高中微积分的技术:积分。
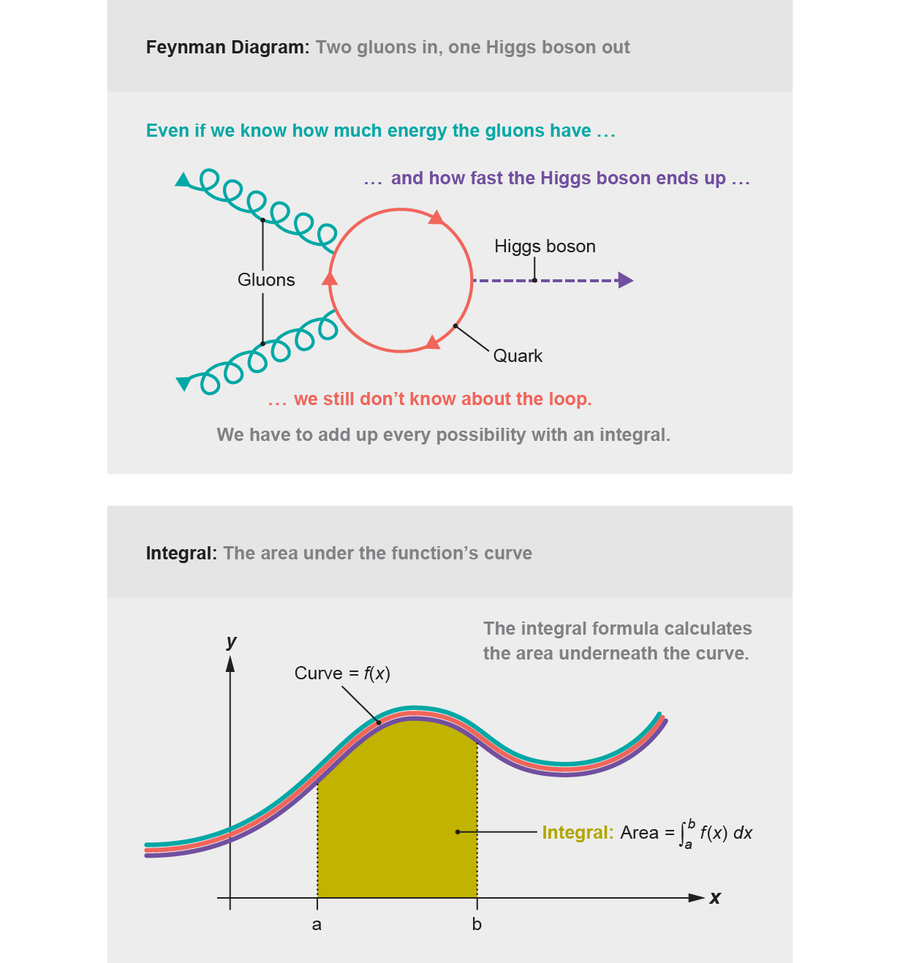
来源:珍·克里斯蒂安森
原则上,要计算散射振幅,我们必须绘制每个可能连接我们粒子的图,即起始成分可能变成最终产品的每种方式(这里是一对胶子和一个希格斯玻色子)。那有很多图,实际上是无限多的图:我们可以随意地在环路内不断绘制环路,每次都需要我们计算越来越复杂的积分。
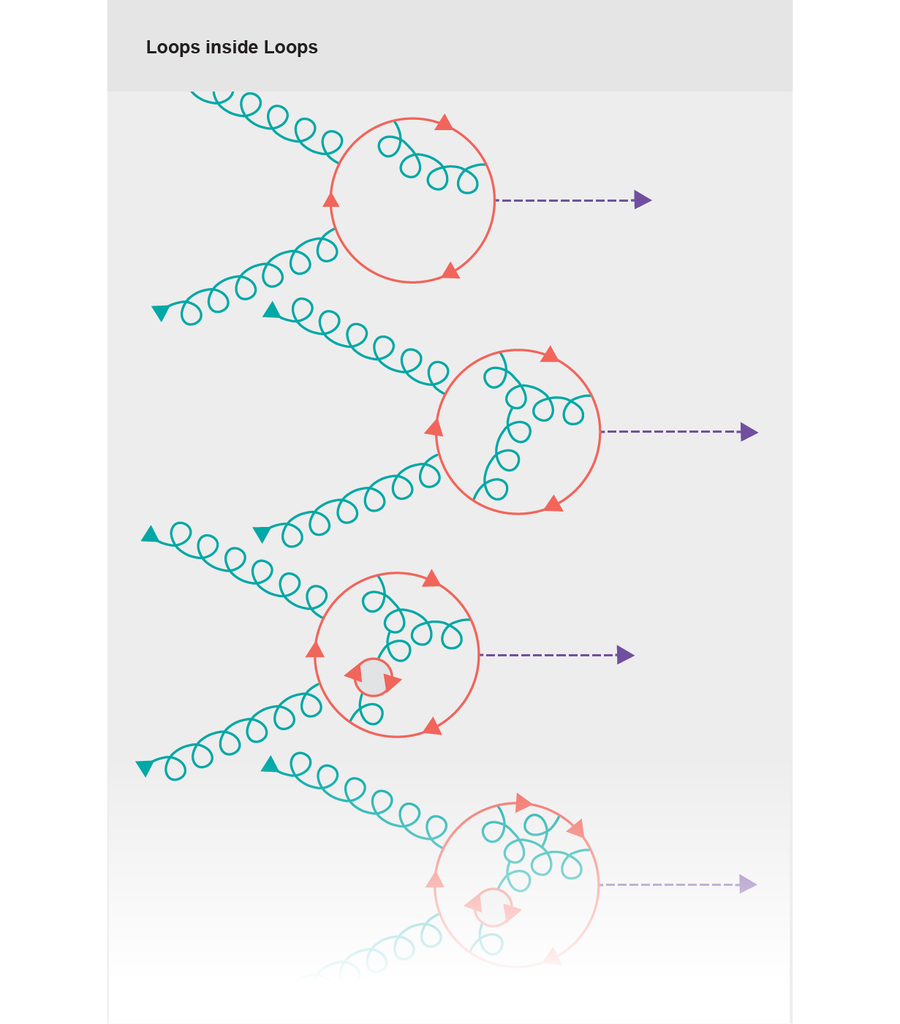
来源:珍·克里斯蒂安森
实际上,我们得救于大多数量子力的低强度。当图中的一组线连接时,它描绘了不同类型粒子之间的“相互作用”。每次发生这种情况时,我们都必须乘以一个常数,该常数与使粒子相互作用的力强度有关。如果我们想绘制一个带有更多闭环的图,我们必须连接更多的线,并乘以更多的这些常数。对于电和磁,相关常数很小:对于你添加的每个环路,你大约除以137。这意味着环路越来越多的图在你最终答案中所占的比例越来越小,最终这一部分变得非常小,以至于实验无法检测到它。关于电和磁的最仔细的实验精确到惊人的小数点后10位,这是科学界最精确的测量之一。达到这个程度“仅”需要四个环路,四个1/137的因子,之后你计算的数字就太小而无法测量了。在许多情况下,这些数字实际上已被计算出来,并且小数点后10位都与实验结果一致。
强核力是一种更难对付的野兽。它是将质子和中子以及它们内部的夸克粘合在一起的力。它比电和磁强得多:对于LHC的计算,每个环路意味着不是除以137而是除以10。要达到10位数字的精度,将意味着绘制10个环路。
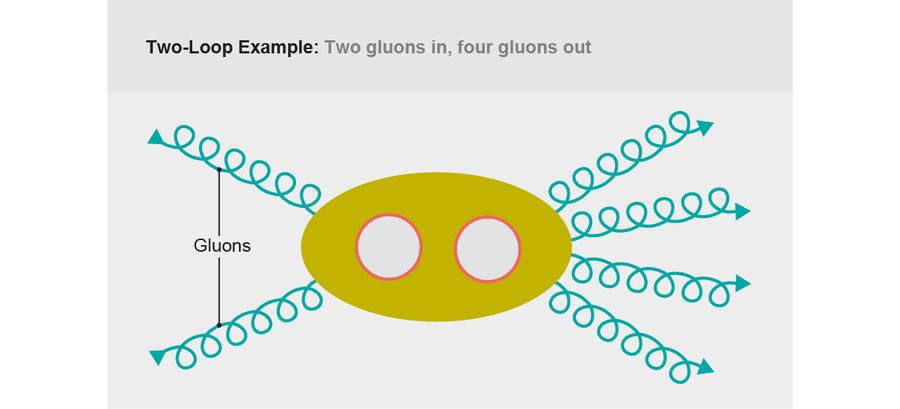
来源:珍·克里斯蒂安森
LHC的精度不如那些电和磁实验。目前,该机器的测量结果刚刚开始与双环路计算的精度相匹配。尽管如此,这些结果已经相当混乱。例如,2010年物理学家维托里奥·德尔杜卡、克劳德·杜尔和弗拉基米尔·斯米尔诺夫进行的一项双环路计算,计算了两个胶子碰撞并产生四个胶子的几率。他们使用简化的理论,带有一些特殊的快捷方式进行了计算,结果公式仍然长达17页复杂的积分。这个长度并不令人惊讶;每个人都知道双环路计算很困难。
直到几个月后,另一组人设法用两行写出了相同的结果。那个小组是三位物理学家——马库斯·斯普拉德林、克里斯蒂安·韦尔古和阿纳斯塔西娅·沃洛维奇——和一位数学家亚历山大·B·冈察洛夫的合作。他们使用的技巧非常强大,它使振幅学家接触到一个我们大多数人以前从未见过的数学领域,这个领域推动了我的职业生涯至今。
周期和对数
给像冈察洛夫这样的数学家展示费曼图中得到的积分之一,你首先会听到的是:“那是一个周期。”
周期是一种数字类型。你可能熟悉自然数(1、2、3、4 ...)和有理数(分数)。2的平方根不是有理数——你不能通过除以两个自然数得到它。然而,它是代数的:你可以写一个代数方程,比如x2 = 2,其中2的平方根是解。周期是更上一层楼:尽管你并不总是能从代数方程中得到它们,但你总是可以从积分中得到它们。
为什么要称它们为周期?在最简单的情况下,那确实就是它们的含义:某事物重复之前的距离。回想高中,你可能还记得与正弦和余弦作斗争。你甚至可能记得,你可以使用欧拉公式将它们与虚数(负数的平方根——换句话说,通常不存在的数字)组合在一起:eix = cos (x) + i sin (x)(这里e是一个常数,i是−1的平方根)。所有这三个——sin (x), cos (x), 和 eix——都有周期 2π:如果你让x从0到2π,函数会重复,你会再次得到相同的数字。

来源:珍·克里斯蒂安森
2π是一个周期,因为它是在eix重复之前的距离,但你也可以将其视为一个积分。在复平面中绘制eix的图形:虚数在一个轴上;实数在另一个轴上。它形成一个圆。如果你想测量圆的长度,你可以用积分来完成,将周围的每个小段加起来。这样做,你会发现正好是 2π。
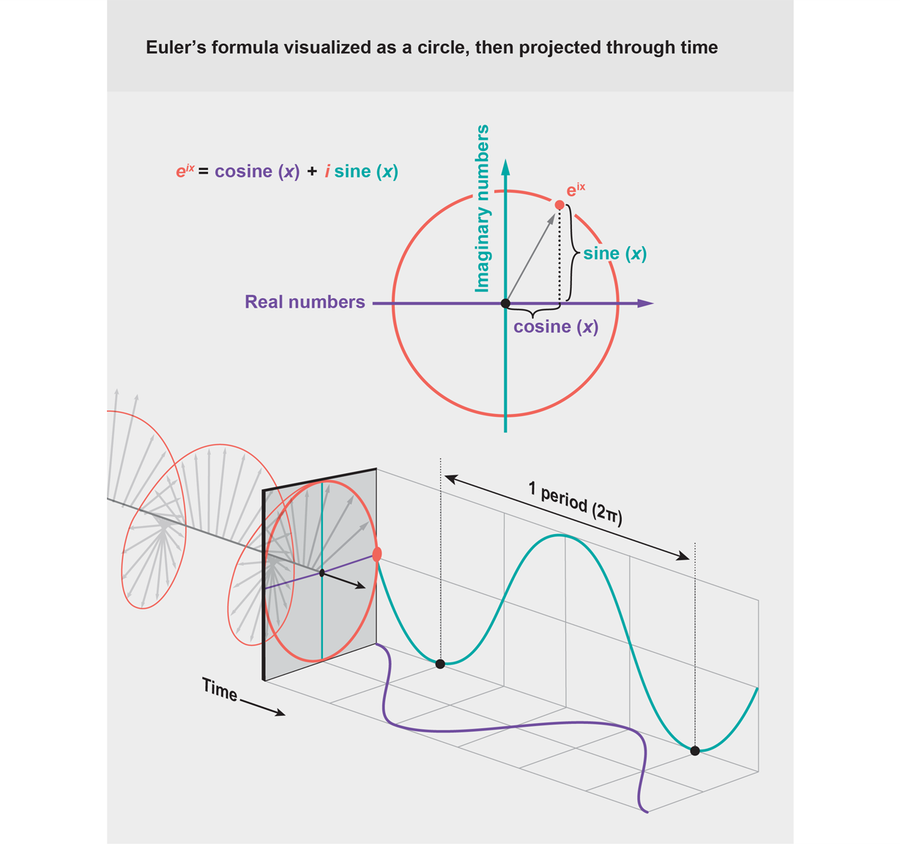
来源:珍·克里斯蒂安森 *
如果你绕圆走一部分,到达某个点 z 会发生什么?在这种情况下,你必须解方程 z = eix。再次回想高中,你可能还记得你需要什么来解这个方程:自然对数,ln (z)。对数可能看起来不像 2π 那样的“周期”,但因为你可以从积分中得到它们,数学家也称它们为周期。除了 2π,对数是最简单的周期。
数学家和物理学家关心的周期可能比这种情况复杂得多。在1990年代中期,物理学家开始对费曼图中得到的积分中的周期进行分类,并且此后发现了令人眼花缭乱的奇异数字阵列。然而,值得注意的是,高中时的图景仍然有用。许多这些奇异数字,当被视为周期时,可以分解为对数。理解对数,你就可以理解几乎所有其他东西。
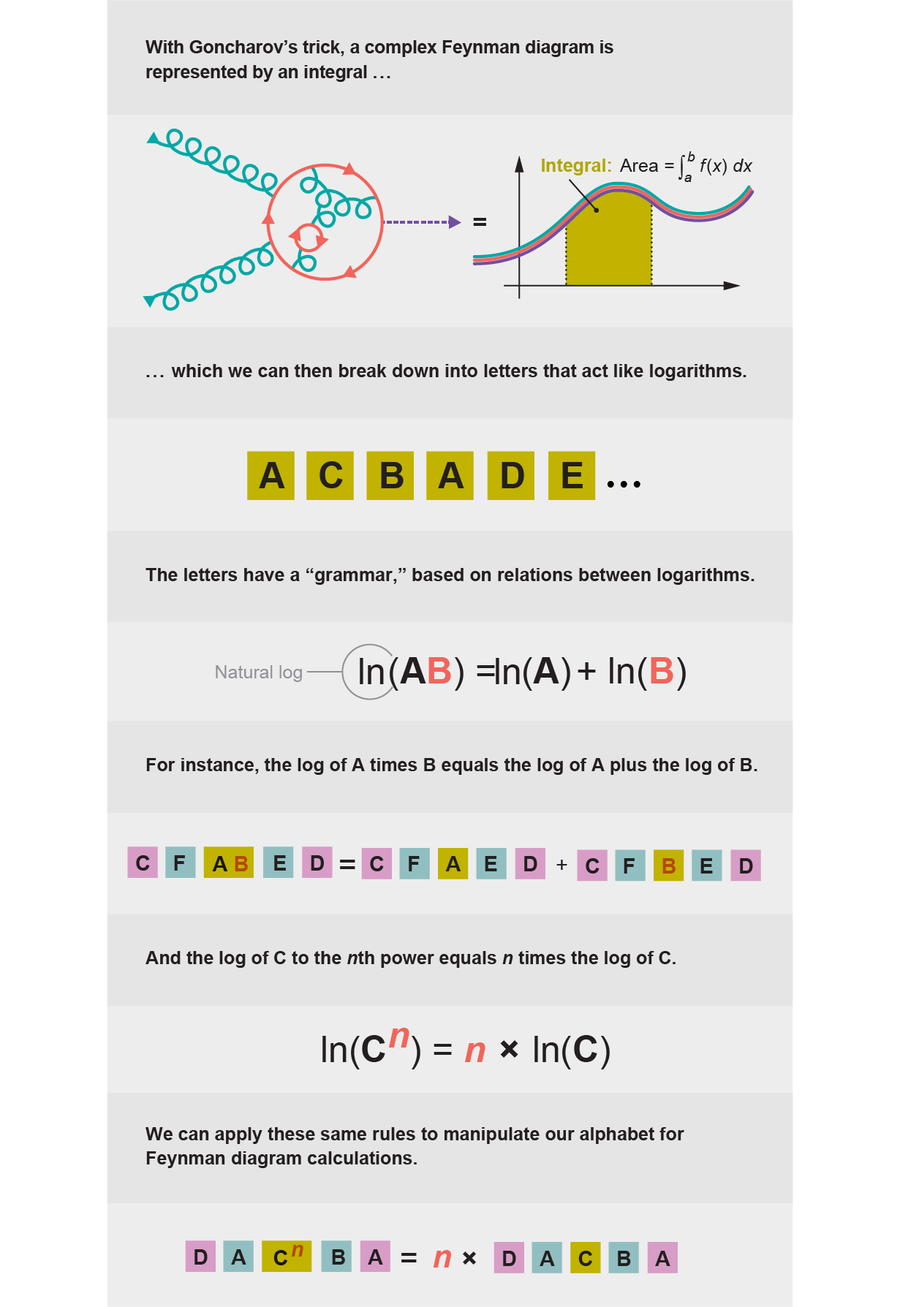
这就是冈察洛夫教给斯普拉德林、韦尔古和沃洛维奇的秘密。他向他们展示了如何将德尔杜卡、杜尔和斯米尔诺夫的17页乱麻分解成一种对数的“字母表”。该字母表遵循基于对数之间关系的自身“语法”,通过使用这种语法,物理学家能够用仅仅几个特殊的“字母”重写结果,使混乱的粒子物理计算看起来简洁得多。
来源:珍·克里斯蒂安森
概括地说,物理学家使用费曼图计算散射振幅,这需要做积分。这些积分总是周期,有时是复杂的周期,但我们通常可以使用冈察洛夫的技巧将这些复杂的周期分解成更简单的周期(对数),这正是点燃我的振幅学领域的原因。我们可以将我们使用的许多积分划分为一个表现得像对数的字母表。并且适用于对数的相同规则,例如 ln(xy) = ln(x) + ln(y) 和 ln(xn) = n × ln(x) 等基本定律,也适用于该字母表。
文字游戏
如果冈察洛夫的字母表技巧所做的只是节省期刊空间,那它就不会那么令人印象深刻了。一旦我们知道了正确的字母表,我们也可以进行新的计算,那些原本不可能进行的计算。实际上,知道字母表让我们可以跳过费曼图,直接猜测答案。

来源:珍·克里斯蒂安森
想想报纸上的主要内容,文字游戏。这个谜题告诉你你需要哪些字母,以及这个词应该有多长。如果你很懒,你可以让电脑写下所有可能的字母顺序,然后浏览列表。最终你会找到一个有意义的词,你就会得到你的答案。
然而,可能的列表可能会很长。幸运的是,在物理学中,我们从提示开始。我们从一个描述我们粒子可能具有的属性(例如它们的能量和速度)的对数字母表开始。然后我们开始用这个字母表写单词,代表最终答案中可能出现的积分。某些单词在物理意义上没有意义:它们描述了实际上不存在的粒子或不可能绘制的图。其他单词是解释我们已经知道的事情所必需的:当粒子变得非常慢或非常快时会发生什么。最后,我们可以将事物从可能是数百万个单词减少到数千个,然后是数十个,最后只有一个独特的答案。从猜测开始,我们最终得到唯一可能的单词,它可以作为我们的散射振幅。
兰斯·J·迪克森、詹姆斯·M·德拉蒙德和约翰内斯·亨恩在2011年使用了这种技术,找到了三环路计算的正确“单词”。我于2013年加入了该团队,当时我从长岛的研究生院偷偷溜走,在斯坦福大学SLAC国家加速器实验室为迪克森工作过冬。与当时的博士生杰弗里·彭宁顿一起,我们将结果变成了我们可以与德尔杜卡、杜尔和斯米尔诺夫的旧双环路计算进行比较的形式。现在,我们不再是17页,而是一个800页长的公式——而且所有这些都没有绘制一张费曼图。
从那时起,我们已经推进到更多的环路,我们的合作也扩大了,杜尔、安德鲁·麦克劳德、西蒙·卡隆-休特、乔治奥斯·帕帕塔纳西奥和法尔科·杜拉特加入了团队。我们现在是七环路,我不知道新的公式需要多少页才能写完。当计算如此复杂时,冈察洛夫的技巧不足以简化结果。在这里,我们很高兴它使计算成为可能!我们现在将我们的结果存储在计算机文件中,这些文件大到你可能会认为它们是视频文件,而不是文本。
椭圆前沿
回想一下,你在散射振幅计算中包含的环路越多,你的预测就越精确。七环路将比LHC可以测量的两个左右的环路更精确,比量子电动力学中最先进的四环路更精确。然而,我在这里说“将是”,因为有一个问题:我们的七环路计算使用了一个“玩具模型”——一个比任何可以描述真实世界的粒子相互作用的理论更简单的理论。升级我们的计算,使其描述现实将是困难的,并且存在许多挑战。其中之一,我们将需要理解称为椭圆积分的东西。
我们使用的玩具模型表现良好。它更令人愉悦的特性之一是,对于我们所做的计算类型,冈察洛夫的方法总是有效:我们总是可以将积分分解成对数的字母表,即圆上的积分。在现实世界中,这种策略在双环路时会遇到问题:两个积分可能会缠绕在一起,以至于无法分离。
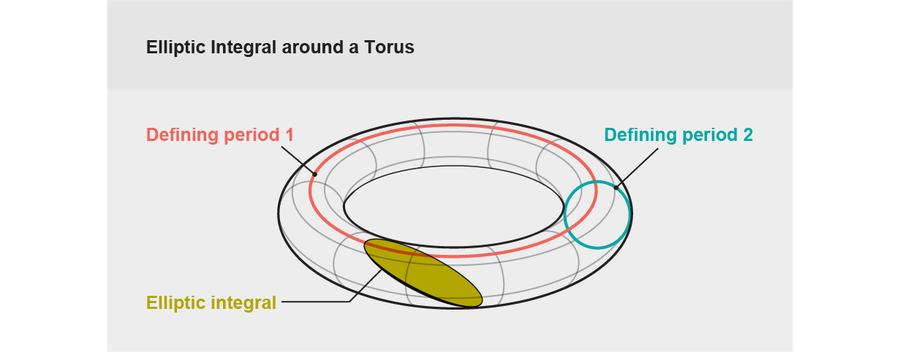
想想两个钩在一起无法拉开的环。如果你将一个环绕着另一个环移动,你将绘制一个甜甜圈形状,或一个环面。一个环面有两个“周期”,两种不同的方式可以在其周围画一条线,对应于两个不同的环。围绕一个圆本身积分,你会得到一个对数。尝试在环面周围画一个环,你不会总是得到一个圆:相反,你可能会得到一个椭圆。我们称这种围绕环面的积分为椭圆积分——椭圆曲线上的积分。
来源:珍·克里斯蒂安森
理解椭圆曲线涉及一些著名的复杂数学问题。其中一些问题非常难以解决,以至于像国家安全局这样的组织使用它们来编码机密信息,假设没有人能足够快地解决它们来破解代码。我们感兴趣的问题并没有那么棘手,但仍然很棘手。然而,随着LHC的精度不断提高,椭圆积分变得越来越重要,促使世界各地的团队着手解决新的数学问题。该机器于2018年底关闭进行升级,但科学家们仍然有大量数据需要整理;它将于2021年重新启动,并将产生比以前多10倍的碰撞。
有时,该领域发展的速度让我喘不过气来。去年冬天,我在普林斯顿大学与一组合作者:麦克劳德、斯普拉德林、雅各布·布尔贾伊利和马蒂亚斯·威廉姆一起隐居。在两周内,我们从一个草拟的提纲到一篇完整的论文,计算了一个涉及椭圆积分的散射振幅。这是我写论文最快的一次,而且整个过程中我们都担心会被抢先,另一个小组会先完成计算。
我们最终没有被抢先。但不久之后,我们收到了一份早期的圣诞礼物:杜尔、杜拉特、约翰内斯·布罗德尔和洛伦佐·坦克雷迪的两篇论文,它们解释了一种处理这些积分的更好方法,这是基于数学家弗朗西斯·布朗和安德烈·列文的工作。这些论文,以及后来与布伦达·佩南特合作的一篇论文,给了我们我们需要的缺失部分:一个新的“椭圆字母”字母表。
有了这样的字母表,我们可以将冈察洛夫的技巧应用于更复杂的积分,并开始理解双环路振幅,不仅在玩具模型中,而且在现实世界中也是如此。
如果我们能在现实世界中进行双环路计算,如果我们能弄清楚标准模型预测到什么新的精度水平,我们将能够看到LHC的数据是否与这些预测相匹配。如果它不匹配,我们将得到一个暗示,表明正在发生一些真正的新事物,一些我们的理论无法解释的事物。这可能是我们将粒子物理学推向下一个前沿,解锁那些我们似乎无法破解的持久谜团所需的一条数据。
*编者注(2019年2月27日):此图在发布后进行了更正。印刷版中的原始图不准确地表示了余弦(x)的曲线。
