财富不平等现象正以惊人的速度升级,不仅在美国,而且在俄罗斯、印度和巴西等国家也是如此。投资银行瑞士信贷的数据显示,全球最富有的1%人口所持有的家庭财富份额,从2008年金融危机到2018年间,从42.5%上升至47.2%。换句话说,截至2010年,388个人的家庭财富总和与世界人口的后一半(约35亿人)相当;今天,乐施会估计这个数字为26人。几乎所有测量家庭财富的国家的调查统计数据都表明,财富正变得越来越集中。
尽管不平等的根源一直备受争议,但物理学家和数学家(包括我在塔夫茨大学的团队)开发的一种方法表明,这些根源长期以来一直隐藏在众目睽睽之下——在一种众所周知的算术怪癖中。这种方法使用统称为基于代理的财富分配模型,这些模型从两个“代理”或行动者之间的个体交易开始,每个代理或行动者都试图优化自己的财务结果。在现代世界中,没有什么比两个人决定交换商品、商定价格并握手更公平或更自然的了。事实上,由个体行动者之间供需平衡产生的经济体系的表面稳定性被认为是启蒙思想的顶峰——以至于许多人已经开始将自由市场与自由本身的概念混为一谈。然而,我们基于自愿交易的看似简单的数学模型表明,现在是时候认真重新审视这种想法了。
特别是,仿射财富模型(之所以如此称呼是因为其数学性质)可以极其精确地描述不同发达国家家庭之间的财富分配,同时揭示一种倾向于集中财富的微妙不对称性。我们认为,这种纯粹的分析方法,类似于X射线,它与其说是为了代表现实世界的混乱,不如说是为了剥离它并揭示潜在的骨架,从而为深入了解当今导致贫困和不平等加剧的力量提供了深刻的见解。
支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
寡头统治
1986年,社会科学家约翰·安格尔首次将财富的流动和分配描述为源于一群“经济主体”(可以是个人、家庭、公司、基金或其他实体)之间的成对交易。到本世纪初,当时都在波士顿大学工作的物理学家斯拉瓦·伊斯波拉托夫、帕维尔·L·克拉皮夫斯基和西德尼·雷德纳,以及现在在星座能源集团的阿德里安·德拉古列斯库和马里兰大学的维克多·亚科文科,已经证明可以使用统计物理学的工具来分析这些基于代理的模型,从而迅速增进我们对其行为的理解。事实证明,许多此类模型发现财富不可阻挡地从一个代理流向另一个代理——即使它们是基于平等行动者之间的公平交易。2002年,当时在印度加尔各答萨哈核物理研究所的阿尼尔班·查克拉博尔蒂引入了后来被称为旧货出售模型的模型,之所以如此称呼是因为它具有真实一对一经济交易的某些特征。他还使用数值模拟来证明它不可阻挡地集中了财富,导致了寡头统治。

图片来源:棕色小鸟设计
为了理解这种情况是如何发生的,假设您在一家赌场,并被邀请玩一个游戏。您必须在桌子上放一些赌注——比如100美元——然后会抛一枚公平的硬币。如果硬币正面朝上,庄家将支付您桌上金额的20%,使桌上金额达到120美元。如果硬币反面朝上,庄家将拿走您桌上金额的17%,使桌上金额剩下83美元。您可以将您的钱留在桌子上,进行任意多次抛硬币(永远不要增加或减少它)。每次玩游戏时,如果硬币正面朝上,您将赢得桌上金额的20%,如果硬币反面朝上,您将损失桌上金额的17%。您应该同意玩这个游戏吗?
您可能会构建两个相当有说服力的论点来帮助您决定该怎么做。您可能会想,“我有½的概率赢得20美元,也有½的概率损失17美元。因此,我的预期收益是
½ x (20美元) + ½ x (-17美元) = 1.50美元
这是正数。换句话说,我的输赢概率是均等的,但如果我赢了,我的收益将大于如果我输了的损失。” 从这个角度来看,玩这个游戏似乎是有利的。
或者,像棋手一样,您可能会进一步思考:“如果我玩10次抛硬币呢?一个可能的结果是其中五次正面朝上,另五次反面朝上。每次正面朝上,我的赌注乘以1.2。每次反面朝上,我的赌注乘以0.83。在任意顺序的五次赢和五次输之后,桌子上剩余的金额将是
1.2 x 1.2 x 1.2 x 1.2 x 1.2 x 0.83 x 0.83 x 0.83 x 0.83 x 0.83 x 100美元 = 98.02美元
因此,我将损失大约2美元的原始100美元赌注。” 再多做一点工作,您就可以确认大约需要93次赢才能弥补91次输。从这个角度来看,玩这个游戏似乎是不利的。
这里提出的两个论点之间的矛盾起初可能看起来令人惊讶,但这在概率和金融领域是众所周知的。然而,它与财富不平等的联系却鲜为人知。为了将赌场的隐喻扩展到(极其简化的)经济中财富的流动,让我们想象一个由1000人组成的系统,他们彼此进行成对交易。让每个人都从一些初始财富开始,这些财富可能完全相等。随机选择两个代理人,让他们进行交易,然后对另外两个代理人做同样的事情,依此类推。换句话说,该模型假设在随机选择的代理人对之间进行顺序交易。我们的计划是在1000人的人口中进行数百万或数十亿次此类交易,看看财富最终是如何分配的。

图片来源:汉娜·巴尔奇克
一对代理人之间的单笔交易应该是什么样的?人们天生厌恶破产,因此我们假设风险金额,我们称之为Δω(Δω发音为“delta w”),只是较贫穷的人绍娜财富的一小部分。这样,即使绍娜在与较富有的人埃里克的交易中输了,她损失的金额也总是少于她自己的总财富。这不是一个不合理的假设,事实上,它捕捉到了大多数人在其经济生活中本能地遵守的自我施加的限制。首先——仅仅因为这些数字对我们来说很熟悉——让我们假设Δω是绍娜财富ω的20%,如果她赢了,则是ω的-17%,如果她输了。(我们的实际模型假设输赢百分比相等,但总体结果仍然成立。此外,增加或减少Δω只会延长时间尺度,以便在我们可以看到最终结果之前需要进行更多交易,最终结果将保持不变。)
如果我们的目标是模拟一个公平且稳定的市场经济,我们应该首先假设没有人具有任何优势,因此让我们通过抛掷一枚公平的硬币来决定w移动的方向。如果硬币正面朝上,绍娜将从埃里克那里获得她财富的20%;如果硬币反面朝上,她必须将她财富的17%给予埃里克。现在从总共1000名代理人中随机选择另一对代理人,然后再次这样做。事实上,继续进行一百万次或十亿次。会发生什么?
如果您模拟这个经济体(旧货出售模型的一种变体),您将得到一个非凡的结果:在大量交易之后,一名代理人最终成为“寡头”,几乎掌握了经济体的所有财富,而其他999名代理人最终几乎一无所有。人们最初拥有多少财富并不重要。所有抛硬币都是绝对公平的也不重要。较贫穷的代理人在每次交易中的预期结果为正,而较富有的代理人的预期结果为负也不重要。这个经济体中的任何单个代理人都可能成为寡头——事实上,如果他们最初拥有相等的财富,则所有人都有均等的机会。从这个意义上说,机会是平等的。但他们中只有一个人确实成为了寡头,而所有其他人的平均财富都随着他们进行越来越多的交易而趋于零。更糟糕的是,某人的财富排名越低,下降速度就越快。
这个结果尤其令人惊讶,因为它即使在所有代理人最初都拥有相同财富并且受到对称对待的情况下也成立。物理学家将这种现象描述为“对称破缺”[参见下文的“不平等的物理学”]。第一次抛硬币就将资金从一个代理人转移到另一个代理人,从而在两者之间建立起不平衡。一旦我们在财富方面存在一些差异(无论多么微小),随后的交易将系统地将财富“涓滴”向上移动,从较贫穷的代理人流向较富有的代理人,从而放大不平等,直到系统达到寡头统治的状态。
如果经济体最初是不平等的,那么最贫穷的代理人的财富可能会下降得最快。它去了哪里?它一定流向了较富有的代理人,因为没有更贫穷的代理人了。对于第二贫穷的代理人来说,情况也好不到哪里去。从长远来看,除了最富有的代理人之外,这个经济体中的所有参与者都将看到他们的财富呈指数级衰减。在2015年的独立论文中,我和我在塔夫茨大学的同事以及巴黎第一大学的克里斯托夫·乔罗提供了查克拉博尔蒂的模拟已经揭示的结果的数学证明——旧货出售模型不可阻挡地将财富从一边转移到另一边。
这是否意味着较贫穷的代理人永远不会赢,或者较富有的代理人永远不会输?当然不是。再次强调,这种设置类似于赌场——您有输有赢,但您在赌场待的时间越长,您就越有可能输。自由市场本质上是一个您永远无法离开的赌场。当早些时候描述的财富涓滴(在每笔交易中从穷人流向富人)乘以世界上77亿人每年进行无数次交易时,涓滴变成了洪流。由于看似无害但略有偏差的交易的集体效应,不平等必然会变得更加明显。
财富的凝聚
当然,您可能会想知道,即使这个模型在数学上是准确的,它与现实有什么关系。毕竟,它描述了一个完全不稳定的经济体,该经济体不可避免地退化为完全的寡头统治,而世界上没有完全的寡头统治。诚然,仅凭旧货出售模型无法解释经验财富分配。为了解决这个缺陷,我的团队以三种方式改进了它,使其更贴近现实。
2017年,我和塔夫茨大学的阿德里安·德维特-李、梅雷克·约翰逊、李杰、杰里米·马克、王洪燕一起,将财富再分配纳入其中。为了与应用数学模型中期望的简洁性保持一致,我们通过让每个代理人在每次交易后都向社会平均财富迈出一步来实现这一点。步幅的大小是他或她与平均值距离的某个分数χ(或“chi”)。这相当于对富人征收统一的财富税(税率为每单位时间χ),并对穷人提供补充补贴。实际上,它将财富从高于平均水平的人转移到低于平均水平的人。我们发现,这种简单的修改稳定了财富分配,从而不再导致寡头统治。令人惊讶的是,它使我们的模型能够以优于2%的精度匹配1989年至2016年间美国和欧洲财富分配的经验数据。单个参数χ似乎概括了许多现实世界的税收和补贴,这些税收和补贴如果单独包含在像这样的骨架模型中,将过于混乱。
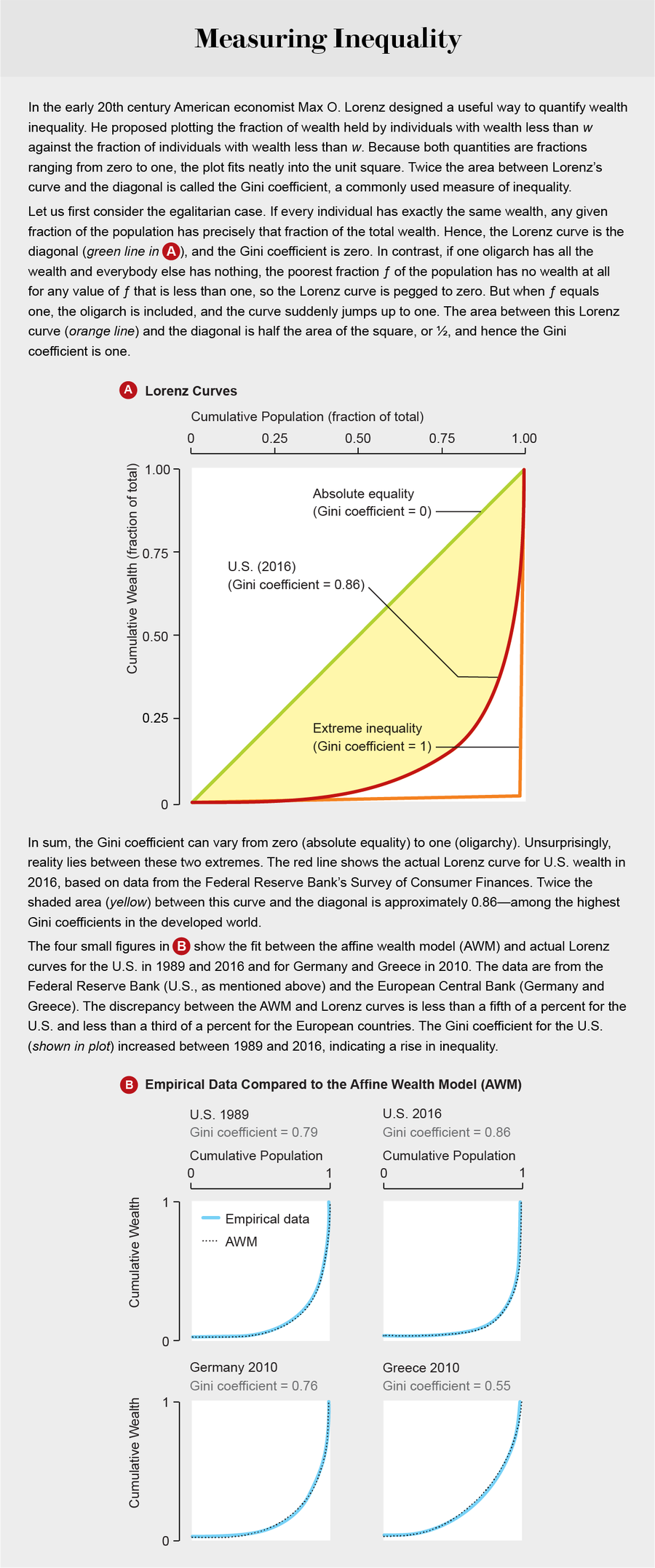
图片来源:珍·克里斯蒂安森
此外,有充分的证据表明,富人享有系统性的经济优势,例如贷款利率较低和更好的财务建议,而穷人则遭受系统性的经济劣势,例如发薪日贷款人和没有时间货比三家以获得最优惠的价格。正如詹姆斯·鲍德温曾经观察到的那样,“任何与贫困作斗争过的人都知道贫穷是多么昂贵。” 因此,在上面提到的同一篇论文中,我们考虑了我们称之为财富获得的优势的因素。我们根据一个新的参数ζ(或“zeta”)乘以财富差除以平均财富的量,使硬币抛掷偏向富有的个人。这种相当简单的改进,可以作为有利于富人的多种偏见的代表,提高了模型与实际财富分配上尾部之间的一致性。
纳入与财富相关的偏见也产生了——并为部分寡头统治现象给出了精确的数学定义。只要财富获得的优势的影响超过再分配的影响(更准确地说,只要ζ超过χ),一小部分人将拥有社会财富的有限部分,1 − χ/ζ。部分寡头统治的出现实际上是另一个经济交易模型的相变,最早由现在的巴黎综合理工学院的让-菲利普·布查德和巴黎高等师范学院的马克·梅扎德在2000年描述。在我们的模型中,当ζ小于χ时,系统只有一个没有寡头统治的稳定状态;当ζ超过χ时,一个新的寡头统治状态出现并成为稳定状态[参见上图]。由此获得的两参数(χ和ζ)扩展旧货出售模型可以以1%到2%的精度匹配1989年至2016年间美国和欧洲财富分配的经验数据。
这种相变可能在前苏联于1991年解体后财富凝聚中发挥了关键作用。对前苏联各加盟共和国实施所谓的休克疗法经济学,导致其政府大幅减少财富再分配(即降低χ),并因突然的私有化和放松管制而导致财富获得的优势(增加ζ)随之跃升。由此导致的“温度”χ/ζ的降低使这些国家进入财富凝聚状态,因此以前的共产主义国家几乎在一夜之间变成了部分寡头统治国家。至少到目前为止,前苏联15个加盟共和国中至少有10个可以准确地描述为寡头统治国家。
作为第三个改进,我们在2019年将负财富(现代经济体更令人不安的方面之一)纳入我们的模型。例如,在2016年,大约10.5%的美国人口因抵押贷款、学生贷款和其他因素而背负净债务。因此,我们引入了第三个参数κ(或“kappa”),它向下移动财富分配,从而解释了负财富。我们假设最贫穷的代理人在任何时候可能拥有的最少财富为–S,其中S等于κ乘以平均财富。在每次交易之前,我们向两位代理人都借出财富S,以便他们都拥有正财富。然后,他们根据前面描述的扩展旧货出售模型进行交易,之后他们都偿还了S的债务。
由此获得的三参数(χ、ζ、κ)模型,称为仿射财富模型,可以以不到六分之一百分点的精度匹配美国财富分配的经验数据,跨越三十年。(在数学中,“仿射”描述的是乘法缩放和加法平移的事物。在这种情况下,模型的某些特征,例如Δω的值,与代理人的财富成比例地缩放,而其他特征,例如S的加法或减法,则是“财富空间”中的加法平移或位移。)与2010年欧洲财富分配数据的吻合度通常优于三分之一到一半的百分点[参见下文的方框]。
为了获得这些与实际数据的比较,我们必须解决“逆问题”。也就是说,给定经验财富分配,我们必须找到参数(χ、ζ、κ)的值,在这些值下,我们模型的结果最接近地匹配它。仅举一个例子,2016年美国户均财富分配最好描述为χ = 0.036,ζ = 0.050和κ = 0.058。仿射财富模型已应用于来自许多国家和时代的经验数据。据我们所知,它比任何其他现有模型都能更准确地描述财富分配数据。
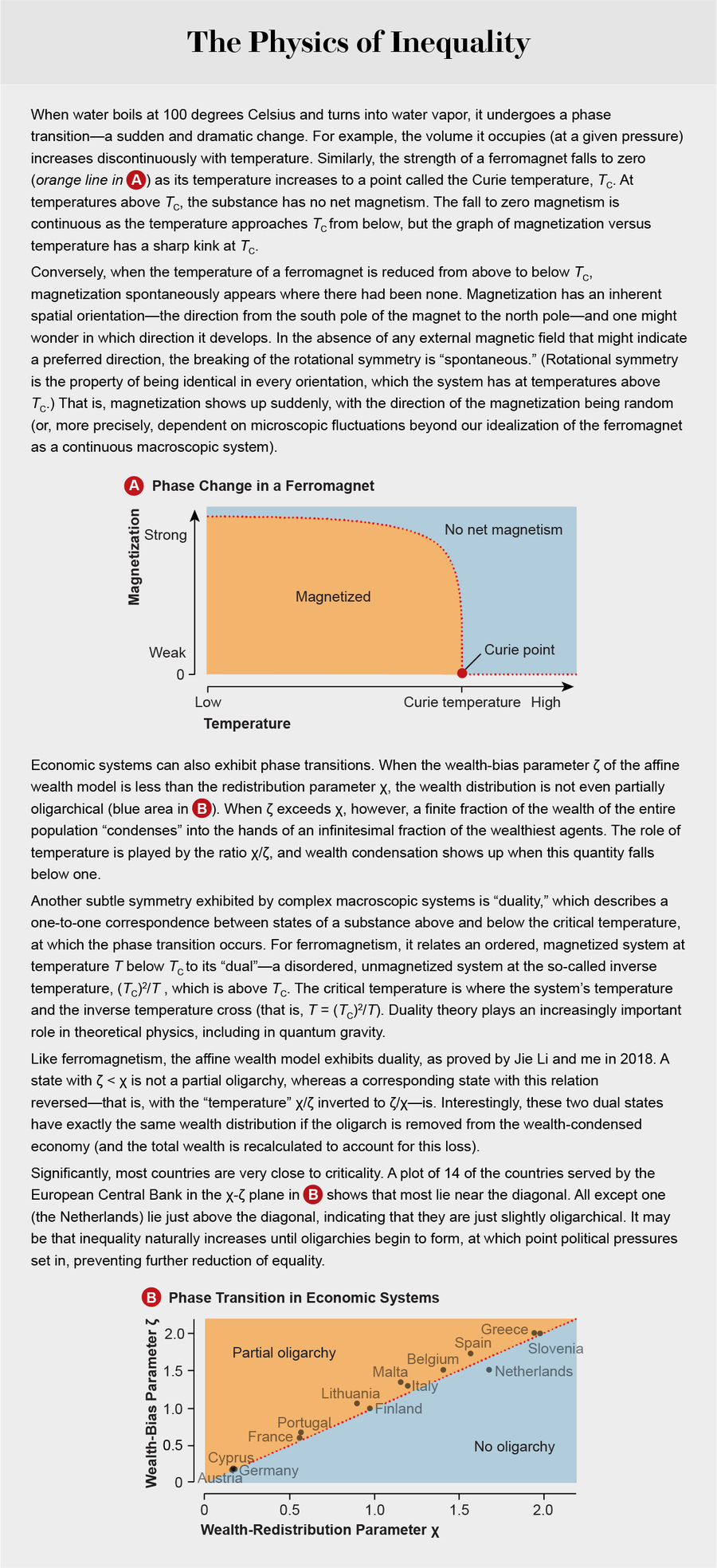
图片来源:珍·克里斯蒂安森;来源:布鲁斯·M·博戈西安;欧洲中央银行(国家数据)
向上涓滴
我们发现值得注意的是,迄今为止发现的最佳拟合经验财富分配模型是一个在没有再分配的情况下将完全不稳定的模型,而不是一个基于市场力量假定均衡的模型。事实上,这些数学模型表明,财富远非向下涓滴到穷人,财富的自然倾向是向上流动,因此自由市场经济中“自然”的财富分配是完全的寡头统治。只有再分配才能限制不平等。
数学模型还提醒人们,财富分配在很大程度上是由对称破缺、机会和早期优势(例如,继承)造成的。对称破缺的存在驳斥了关于财富不平等的公正性的论点,这些论点诉诸“自愿性”——即个人对其经济结果承担全部责任,仅仅因为他们自愿进行交易——或财富积累必然是聪明才智和勤奋的结果的想法。诚然,个人在财富谱上的位置在一定程度上与这些属性相关,但该谱的总体形状可以用完全忽略这些属性的统计模型以优于0.33%的精度来解释。运气比通常认为的起着更重要的作用,因此现代社会普遍归因于财富的美德——以及同样,归因于贫困的耻辱——是完全没有道理的。
此外,只有精心设计的再分配机制才能弥补市场经济中财富从穷人流向富人的自然趋势。再分配常常与税收混淆,但这两个概念应该完全分开。税收从人民流向政府,以资助这些政府的活动。相比之下,再分配可以由政府实施,但最好将其视为财富从人民流向人民的流动,以补偿市场经济中固有的不公平现象。在统一的再分配计划中,所有拥有低于平均财富的人都将获得净资金,而高于平均财富的人将支付。正因为当前的不平等程度如此极端,因此接受资金的人数将远远多于支付资金的人数。
鉴于真实经济体的复杂性,我们感到欣慰的是,物理学家和数学家开发的简单分析方法以空前的精度和准确性描述了多个国家的实际财富分配。同样令人好奇的是,这些分配显示出复杂物理系统的微妙但关键的特征。然而,最重要的是,对自由市场的草图(像仿射财富模型一样简单且貌似合理)导致产生的经济体绝非自由和公平,这应该既是警钟,也是行动的号召。

