可能的最大自然数是多少? 通过使用“自然”这个词,我已经排除了你简单地回答无穷大 (∞) 来破坏猜谜游戏的可能性。但即使我们允许无限大的值,这个回答也会引起问题。那么 ∞ + 1,∞2 或 ∞∞ 呢? 如果人们提出这些答案来回答最大的自然数问题,谁才是对的?
答案是谁都不对,因为无穷大不是一个普通的数字,它不遵循通常的计算规则。 例如,无论你从 –∞、0 还是 1 开始,数轴都是无限的。 因此,诸如 ∞ + 1 之类的陈述毫无意义。 此外,即使是无限值也存在差异:无穷大并不总是等于无穷大。 因此,无穷大不会是最大数字竞赛中有保证的获胜者。
人类花费了数千年的时间才意识到这个想法并将其铸造成一个简洁的理论。 19 世纪末,数学家格奥尔格·康托尔通过思考数量及其大小,为无穷大的数学概念奠定了基础。 例如,{1, 2, 3, 4} 和 {x, y, z, q} 都由四个元素组成,因此大小为 4,专家称之为“基数为 4”。
支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。 通过购买订阅,您将帮助确保关于塑造我们当今世界的发现和想法的具有影响力的故事的未来。
另一方面,自然数 {0, 1, 2, 3,...} 包含无限多个元素。 我们可以将 1 加到任何自然数上; 结果也是一个自然数。 如果我们现在看一下所有偶数的集合 {0, 2, 4,...},我们可能会认为它只有一半大小——毕竟,只有每隔一个自然数才包含在其中。 但康托尔认识到,这两个集合(自然数和偶数)具有相同的基数。
匹配集合和可数无穷大
正如我在另一篇专栏文章中讨论的那样,当康托尔比较两个集合的元素时,他得出了这个令人惊讶的结果。 如果你想知道集合 A(例如,公交车站的人)是否与另一个集合 B(公交车上的空座位)完全一样大,你可以为 A 中的每个元素分配一个来自 B 的元素。 如果最后还有人站着,那么 A 比 B 大。 另一方面,如果还有空座位,那么 B 必须比 A 大。
但是,如果你可以为每个人精确地分配一个座位,那么这两个集合的大小完全相同,因此具有相同的基数。 通过这种方式,康托尔还研究了无限集合的基数。 例如,你可以将任何自然数精确地映射到一个偶数,例如,通过形成对 (0,0)、(1,2)、(2,4)、(3,6)、...、(n, 2n)。 映射完全有效。 最后既没有留下自然数,也没有留下偶数。 因此,这两个集合包含相同数量的元素。
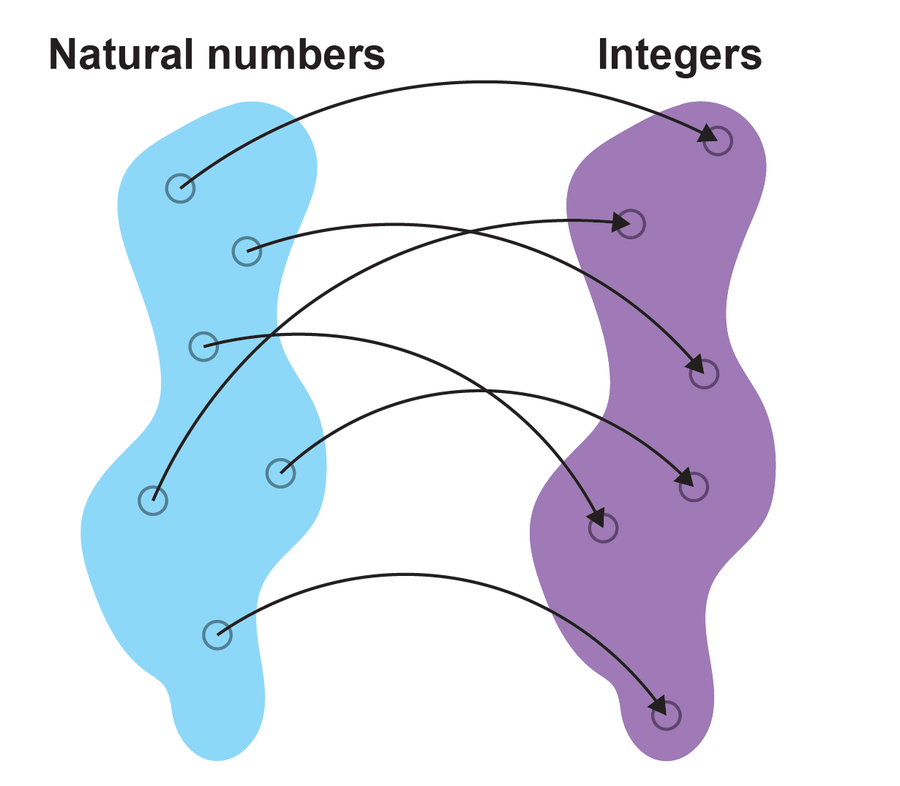
如果两个集合之间存在一对一的映射,则这两个集合相等。 信用:Spektrum der Wissenschaft/Manon Bischoff,大众科学风格
这里出现了一个重要的教训。 当涉及到无穷大时,不要凭直觉行事。 这些想法很少是直观的。
不仅自然数和偶数的基数相同,映射两个集合的技巧也可以应用于其他例子。 例如,所有奇数的集合与所有自然数的集合大小相同——所有整数(包括负值)、素数甚至有理数(包括分数)的集合也是如此。 对于这些集合中的每一个,都存在一个映射,该映射将自然数 {1, 2, 3,...} 唯一地分配给每个元素。 这意味着你可以——至少在理论上——为这些集合的元素编号(如果你有无限的时间和空闲)。
最小的无穷大因此得名。 自然数的基数称为“可数无穷大”,用 ℵ0 (读作“阿列夫零”)表示。 因此,与其在最大数字竞赛中提交答案“无穷大”,不如提供 ℵ0。
到目前为止提出的集合都具有相同的基数。 但实数打破了这个模式。 如果除了有理数之外,你还允许无理数值,例如 2 的平方根、pi 或 蔡廷常数,那么集合突然变得如此之大,以至于你无法再枚举它的元素——即使列表是无限长的。
实数的无穷大超过了自然数
康托尔用他的第二个“对角论证”证明了这个事实。 这是一种反证法:你从假设存在可数无穷多个实数开始,并从这个想法中推导出一个矛盾的陈述(即,“不可能存在可数无穷多个实数”)。
为了继续,你不必考虑所有实数。 假设 0 到 1 之间的所有实数值都是可数的就足够了(我们很快就会看到,这是错误的)。
因此,你可以将所有这些值写在一个无限长的列表中,一个在另一个下面。 例如
0.32476834567854765 ...
0.84737834527845745 ...
0.78347864586745768 ...
0.78347863763547879 ...
...
列表的排序方式无关紧要。 唯一重要的是它是完整的。 如果我们真的可以数出所有的值,那么我们的列表必须包含 0 到 1 之间的每个实数。 但康托尔证明了他可以构造另一个介于 0 和 1 之间的数字,该数字不会出现在列表中。
他是这样做的:新数字的第一位小数对应于列表中第一个数字的第一位小数加一——即上例中的 4。 第二位小数是通过计算第二个数字的第二位小数加一得到的——即 5。 对于第三位,你将第三个数字的第三位小数加 1,依此类推。 (如果你遇到 9,你可以将值更改为 0。)
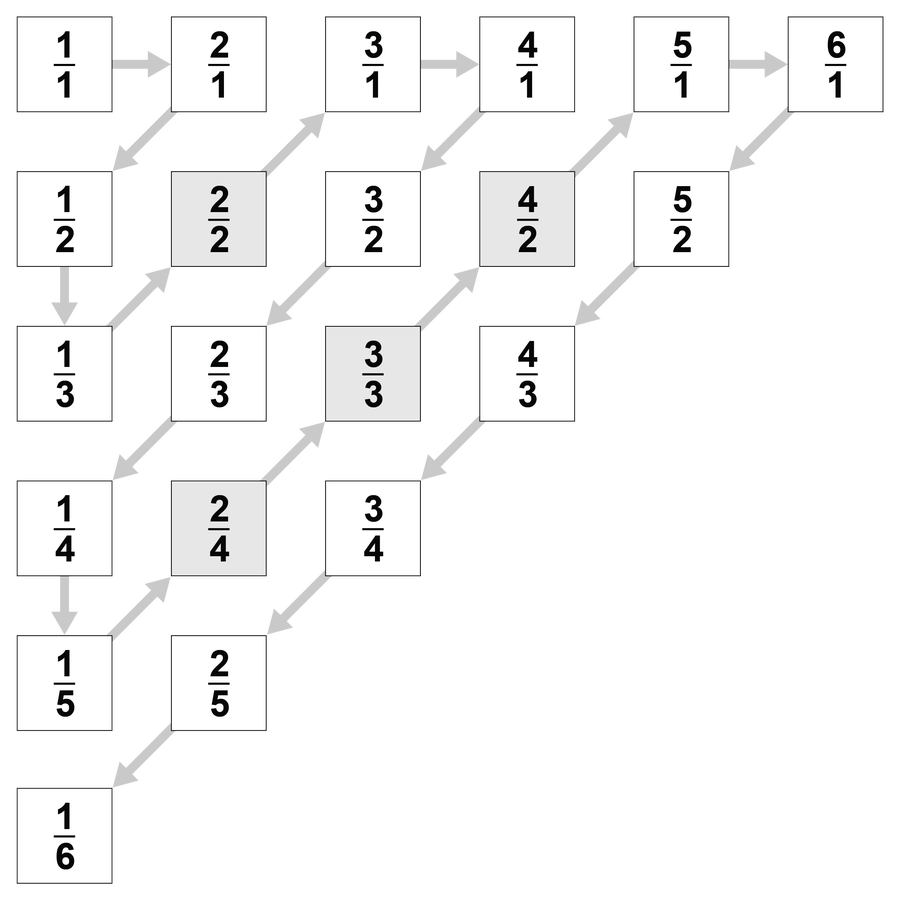
要建立康托尔的对角论证,你可以首先通过遵循箭头并忽略分子大于分母的分数来创建所有有理数的列表。 信用:Buckyball Design; 来源 维基百科
通过这种方式,将获得一个具有无限位小数的无理数。 它不出现在列表中,因为它总是与列表中列出的每个数字至少在一个数字上不同。 因此,列表不可能完整,这与最初的假设相矛盾。 因此,康托尔可以得出结论,存在“不可数”的实数。
一个可证明不可证明的假设
除了自然数的基数 ℵ0 之外,至少还有一个(不可数)无穷大——它可能比 ℵ0 更适合在寻找最大数字的竞赛中获胜。
实数集究竟有多大? 康托尔在调查是否存在一个数字集合,其大小大于自然数但小于实数时,也问了自己同样的问题。 在没有找到这样的集合后,这位数学家在 1878 年提出了他著名的“连续统假设”。 它指出,不存在基数介于自然数和实数之间的集合。
但康托尔无法证明他的假设——任何其他人也无法证明。 事实证明,连续统假设属于我们基本数学框架无法解决的陈述。 它们是可证明不可证明的:你既不能通过通常的数学手段证明也不能证伪这个猜想。 (库尔特·哥德尔证明了在 1931 年,在数学的每个有意义的表述中都存在这种不完备性。)
换句话说,你可以假设连续统假设为真,并且永远不会遇到矛盾。 然而,反过来,你可以假设在自然数和实数的基数之间存在其他无穷大——并且也不会遇到任何问题。 这对于数学家来说并不是特别令人满意。 毕竟,我们讨论的是实数的大小——没有人知道存在多少个这样的值。 作为回应,有些人正试图扩展该学科的基本框架,以便从这个更大的理论中推导出一个工具来证明或证伪连续统假设。
专家们在这个努力上绝非意见一致。 数学的基础——“策梅洛-弗兰克尔集合论”——由九个未经证明的基本陈述(所谓的公理)组成,这些公理构成了整个学科的基础。 花费了几次尝试才找到适合该任务的公理集,因为它必须满足几个要求。 该集合应尽可能少地包含公理,并且它们应直观地为真且不太复杂。 其他示例是空集公理,它声明存在一个没有元素的集合,以及配对公理,根据该公理,具有相同元素的两个集合是相等的。
策梅洛-弗兰克尔集合论的九个公理(连同选择公理)足以构建我们所知道的数学。 但连续统假设避开了它们。 为了更详细地研究实数的基数,你必须扩展当前的集合论以包含其他基本陈述。 例如,你可以将陈述“连续统假设为真”附加到公理组中。 然而,这不会是一个好的公理。 与其他陈述不同,并不直接清楚为什么这个陈述应该是真的。
因此,专家们正在寻找其他直观上为真并且可以用来研究连续统假设的公理。 已经有一些有希望的候选者——有些会证实康托尔的猜想,而另一些会反驳它。 哪种扩展版本的集合论会占上风(如果有的话),仍有待观察。 只要情况如此,实数有多少个仍然是一个未解之谜。
即使这仍然是一个谜,但早已知道存在基数比实数集大得多的集合——即使实数本身是无限的。 如果你想赢得最大数字游戏,你应该去追逐最大的无穷大。
本文最初发表在《光谱》杂志上,并经许可转载。
