沃伦·巴菲特曾经挑战比尔·盖茨进行一场不寻常的骰子游戏。巴菲特在桌子上放了四个骰子,并解释了规则。他们每人选择一个骰子,掷几次,谁掷出的数字更大次数更多,谁就获胜。这些骰子的数字不像标准骰子那样。通常的一到六被其他数字取代,这些数字因骰子而异。作为一种所谓的礼貌,巴菲特邀请盖茨先选骰子。这引起了怀疑,促使盖茨亲自检查骰子,然后坚持让巴菲特先选。
通常,在游戏中先选会带来优势,那么为什么这些大亨争夺第二个选择权呢?答案在于巴菲特骰子的一种特殊属性。为了理解这一点,让我们检查一个与巴菲特使用的骰子具有相同属性但更易于分析的类似骰子的例子。
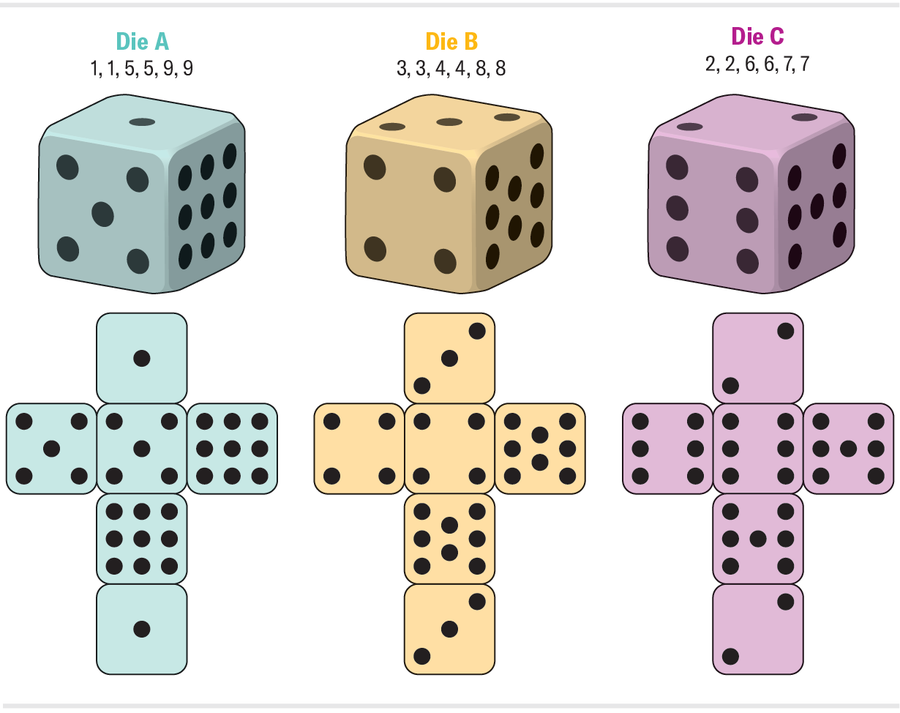
来源:Amanda Montañez
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的有影响力的故事的未来。
骰子 A 比骰子 B 掷出更高数字的频率有多高?由于每个骰子上只有三个不同的数字,三分之一的时间,骰子 A 将掷出 9,无论 B 掷出什么都会获胜。三分之一的时间,A 将掷出 1,无论 B 掷出什么都会输。剩下的三分之一的时间,A 将掷出 5,这将在 B 的三分之二的掷骰中获胜(掷出 3 或 4 的那些)。使用概率规则汇总这些观察结果,我们得到 A 击败 B 的概率为 (⅓ x 1) + (⅓ x 0) + (⅓ x ⅔) = 5/9,约为 56%。类似的计算得出 B 击败 C 的概率也相同。也就是说,B 击败 C 的概率也约为 56%。因此,如果 A 通常击败 B,而 B 通常击败 C,那么 A 肯定通常会击败 C,对吗?错了!C 实际上也击败 A 的概率约为 56%。
我们称这些不守规矩的立方体为非传递骰子。生活中遇到的许多关系都表现出相反的传递性:如果艾丽西亚比布鲁诺年长,而布鲁诺比卡桑德拉年长,那么艾丽西亚比卡桑德拉年长。这是一个有效的推论,因为“比……年长”的关系服从传递性。非传递骰子让我们感到惊讶,因为“通常掷出更高数字”的关系不是传递的,尽管它看起来应该是传递的。请注意,为了平均掷出比骰子 B 更高的数字,骰子 A 不需要总是掷出更高的数字。至关重要的是,A 击败 B 的情况和 A 输给 C 的情况之间存在重叠。面上的数字的这种交错使得非传递性成为可能。
对于任何一组非传递骰子,在巴菲特的游戏中先选的人都处于劣势,因为第二个玩家总是可以选择可能击败对手选择的骰子。许多人最初通过石头剪刀布游戏接触到非传递游戏。其循环获胜结构确保没有一种选择可以唯一地胜过任何其他选择。巴菲特的骰子游戏类似于诱骗你的对手宣布他们打算在石头剪刀布游戏中接下来出什么——这是一个会让他们输掉游戏的错误。
斯坦福统计学家布拉德利·埃夫隆在 50 多年前发明了非传递骰子。埃夫隆的四组骰子中的每个骰子击败另一个骰子的概率令人印象深刻,达到三分之二(约 67%)。马丁·加德纳在他的传奇“数学游戏”专栏中普及了埃夫隆的骰子《大众科学》,但数学爱好者从那时起就设计了许多巧妙的变体。我们现在知道,任意数量的骰子(大于两个)都可以表现出非传递循环,例如,存在一组 26 个骰子,其中骰子 A 通常击败骰子 B,骰子 B 通常击败 C,骰子 C 通常击败 D,依此类推,一直到骰子 Z,尽管骰子 Z 位于一系列占优势骰子的末端,但它却通过循环返回并通常击败 A 来制造冷门。
非传递骰子不必包含六个面。事实上,具有任意数量面(大于两个)的非传递三骰子存在。荷兰谜题制造者奥斯卡·范·德文特甚至发明了一套七个六面骰子,允许三名玩家参与巴菲特的游戏。换句话说,如果巴菲特和盖茨邀请多莉·帕顿与他们一起玩骰子,那么盖茨和帕顿可以各自从七个骰子中选择,而巴菲特仍然总能在剩下的五个骰子中找到一个通常击败他们两人选择的骰子。
就在你认为你已经理解了非传递骰子的奇特行为时,下面这个绝妙的构造会让你再次震惊得说不出话来。
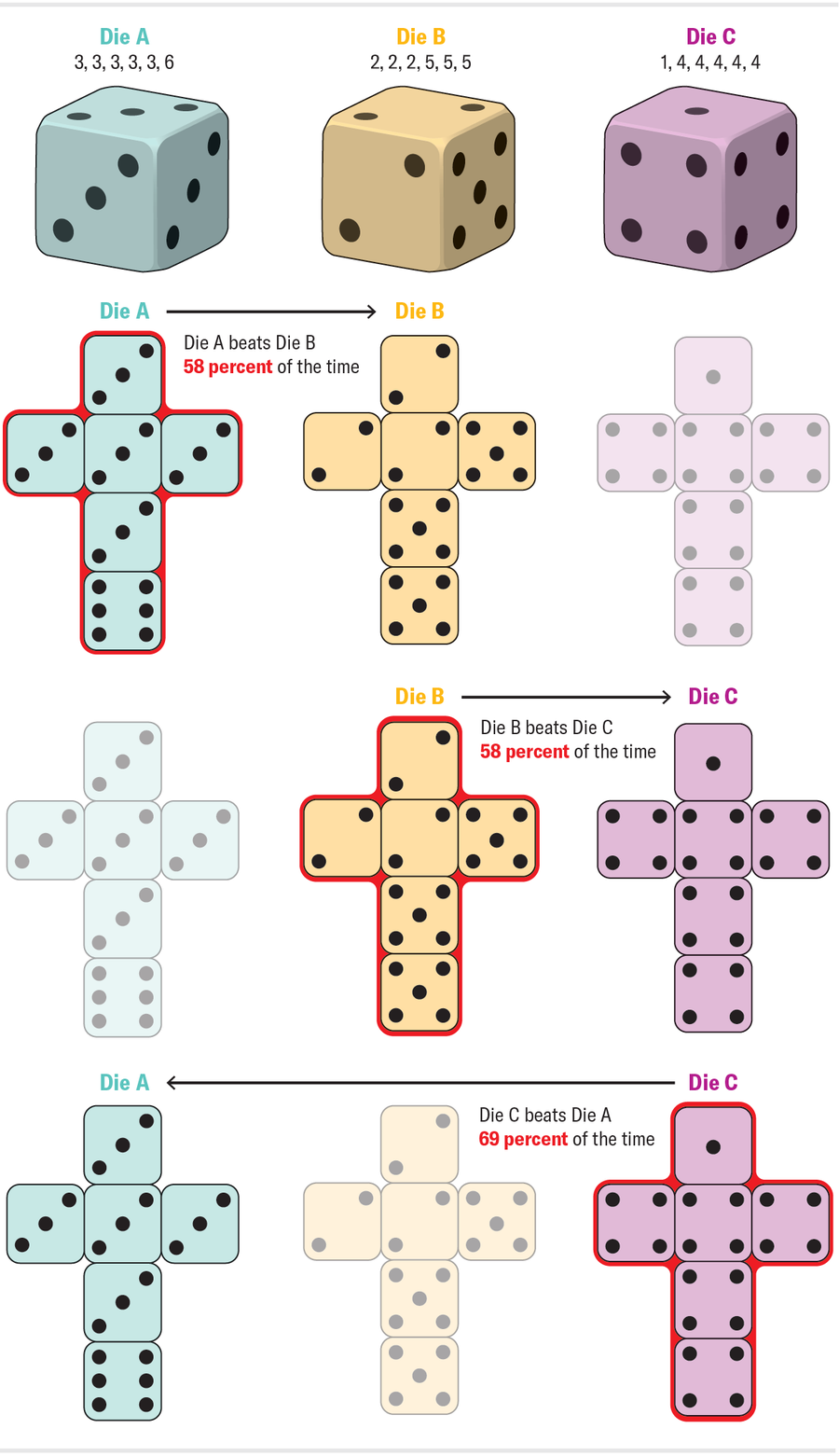
来源:Amanda Montañez
可以计算出 A 击败 B 的概率为 7/12(约 58%);B 击败 C 的概率为 7/12;C 击败 A 的概率为 25/36(约 69%)。到目前为止,没有什么我们以前没见过的。这些骰子彼此击败的概率并不完全相同,但它们仍然是非传递的。骰子通常成对出现。当您想象掷骰子时,您可能会想到手中拿着两个相同的骰子,并将每个骰子上出现的数字相加。如果我们从上图掷出成对的骰子会发生什么?两个骰子 A 掷出的总和击败两个骰子 B 掷出的总和的概率是多少?由于骰子是相同的,它是否与以前相同,或者复制骰子是否会放大 A 对 B 的优势?在一个令人震惊的转折中,效果逆转了。一对骰子 A 通常输给一对骰子 B!更重要的是,整个循环都逆转了:一对骰子 B 通常输给一对骰子 C,而一对骰子 C 通常输给一对骰子 A。购买一套这样的骰子是可靠的被禁止参加家庭游戏之夜的方法。
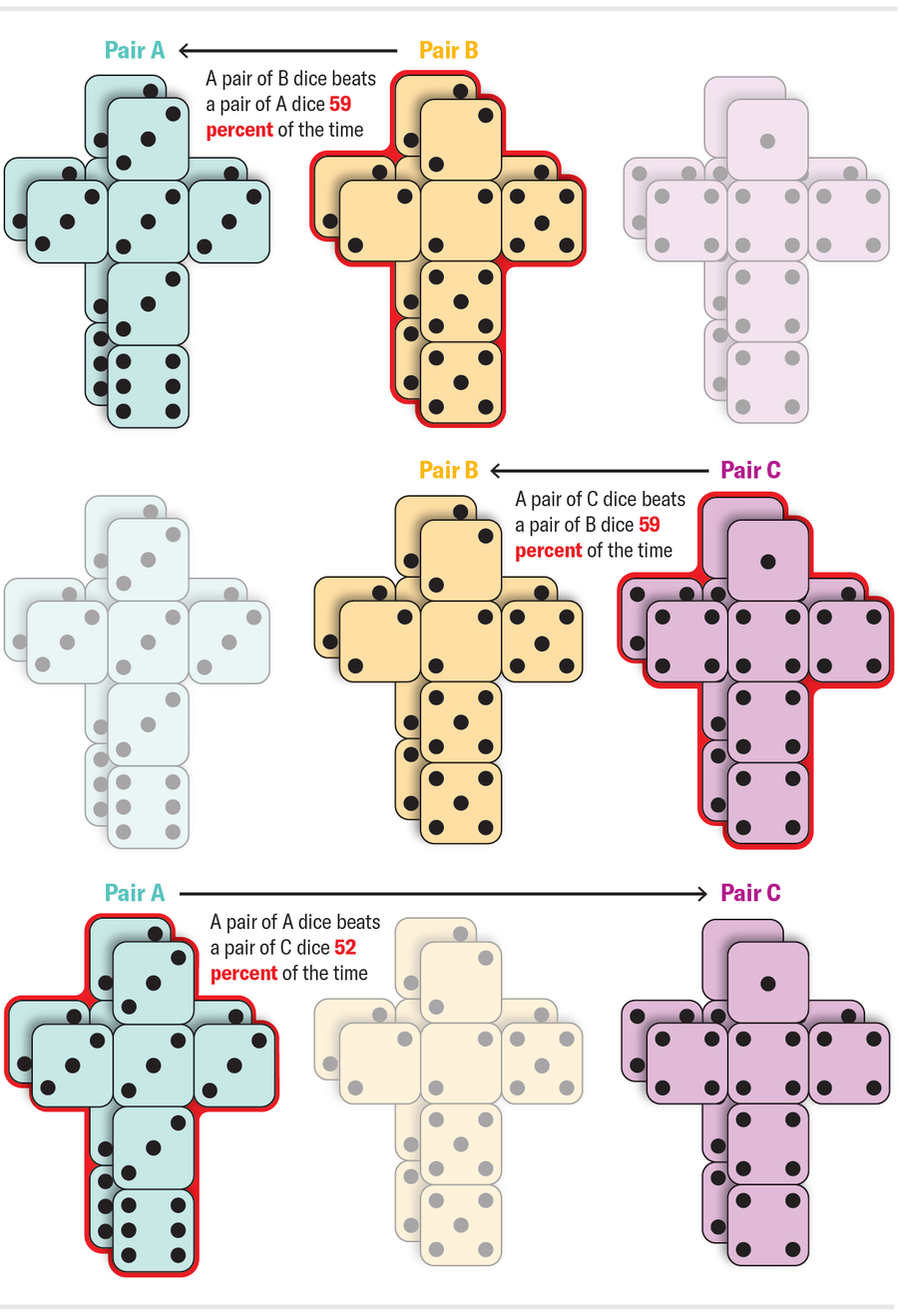
来源:Amanda Montañez
为了感受复制骰子如何逆转它们的相对强度,想象一下两个两面骰子 X 和 Y 的简单情况。X 的两个面都有数字 1,而 Y 的面是 0 和 3。这些骰子的强度相等。Y 有一半的时间获胜(当它掷出 3 时),一半的时间输掉(当它掷出 0 时)。但是,当我们复制骰子时,骰子 Y 对变得比骰子 X 对更强。骰子 X 对总是掷出总共 2。骰子 Y 对只有在它们都掷出 0 时才会输,而这种情况只发生在四分之一的时间。类似的现象解释了上图中的逆转。
非传递骰子应该存在根本不明显。但这是否是因为它们很少见?如果您对一组三个骰子所知甚少,只知道 A 通常击败 B,而 B 通常击败 C,那么 A 通常击败 C 还是反之亦然的可能性更大?聪明的人已经手工精心构造了上面讨论的所有骰子,但是他们是否可以只是随机选择骰子编号,并有很大的机会找到非传递集合?
英国数学家蒂莫西·高尔斯着手回答这个问题。高尔斯领导着Polymath 项目,这是一种创新且相对较新的数学研究范例。Polymath 项目没有像典型的数学研究模型那样,由一两所大学的少数数学家啃硬骨头地解决问题,而是采用了众包方法。任何数量的贡献者都可以通过在线论坛讨论来合作证明。高尔斯认为非传递骰子问题适合集体努力,并于 2017 年在他的博客上提出了这个问题。用 WordPress 评论区取代黑板,数十位头脑风暴了这个问题并破解了它。
如果您随机为三个不同的骰子分配数字,然后想知道它们是否表现出非传递性的概率,这可能取决于您对“随机分配数字”给骰子的确切含义。Polymath 团队使用两个自然标准对此进行了建模。正如典型的六面骰子只包含 1 到 6 之间的数字一样,随机的n面骰子也只包含 1 到n之间的数字(尽管有些可能会重复,有些可能根本不会出现)。此外,典型六面骰子上的数字加起来为 1 + 2 + 3 + 4 + 5 + 6。为了保持骰子的平衡(例如,没有骰子应该包含全部为 1 或全部为巨大数字),Polymath 团队对n面骰子提出了以下要求:它们的面之和应等于从 1 到n的数字之和。
你想猜测传递骰子还是非传递骰子更常见吗?Polymath 项目参与者证明,三个随机的 n 面骰子将大约一半的时间是非传递的。换句话说,知道 A 通常击败 B,而 B 通常击败 C,几乎不能为您提供关于 A 通常会击败 C 还是反之亦然的信息。我本以为传递骰子比非传递骰子更常见。我可以想象一些多疑的读者,厌倦了他们的期望被颠覆,预测非传递骰子比传递骰子更常见。但是这些狡猾的骰子坚持要逃避预测。对于三个骰子,传递骰子和非传递骰子同样常见。
