18世纪,普鲁士城市柯尼斯堡的居民们苦苦思索着一个难题:他们如何才能找到一条穿过城市的步行路线,恰好一次走过其著名的七座桥梁?
这些桥梁横跨一条河流,河流中包含两个大岛。无论他们如何规划路线,都无法避免重复走过一座桥。
这个问题难住了当地的思想家,他们最终写信给著名数学家莱昂哈德·欧拉(发音为“奥伊勒”),恳求他平息他们的好奇心。欧拉不屑一顾地回应道,声称这个问题与“数学几乎没有关系”。在某种程度上,他是对的,因为相关的数学尚未被发明出来。尽管他最初表示拒绝,但欧拉最终还是解决了柯尼斯堡七桥问题,他没有意识到,在这个过程中,他开创了两个新的数学分支。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。 通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和思想的具有影响力的故事的未来。
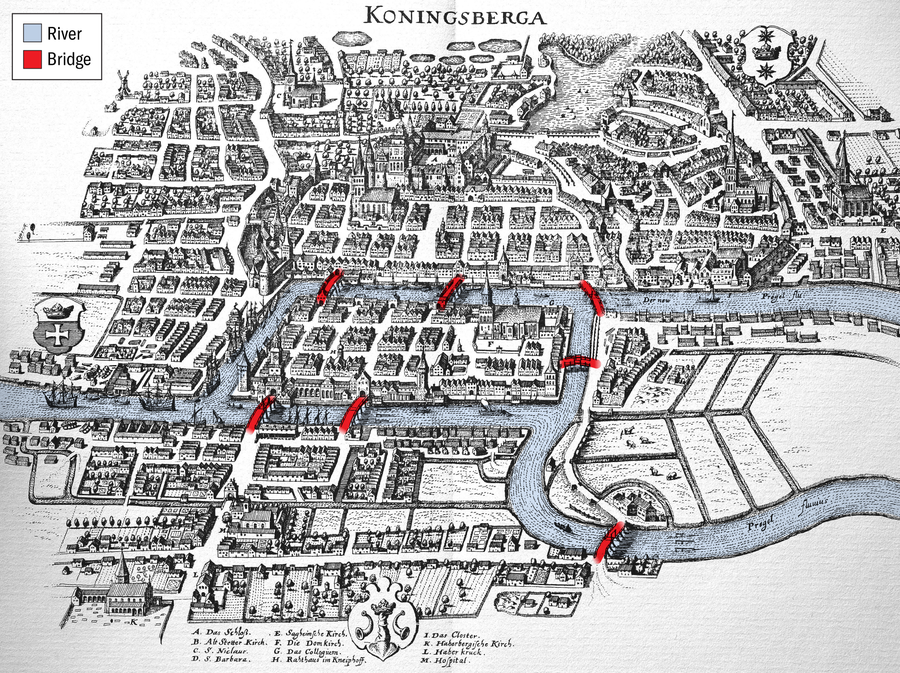
中世纪的普鲁士城市柯尼斯堡,现在是俄罗斯的加里宁格勒。 这张18世纪的城市地图是经过数字增强的复制品,经过修改以突出河流和桥梁。
图片来源:Alamy Stock Photo(地图);阿曼达·蒙塔内斯(突出显示)
假设您是柯尼斯堡的居民。看着上面的地图,您能设计出一条遍历每座桥梁一次的路径吗?您必须像数学家一样思考。解决任何数学问题的第一个障碍是剥离无关信息,直到只剩下必要的要素,这个过程称为抽象。地图的许多特征并不影响手头的问题。桥梁的长度、陆地的大小,甚至陆地和桥梁的地理方位都可以忽略不计。重要的是哪些陆地块与哪些其他陆地块相连,以及连接多少次。现在我们可以创建一个更简单的图表,仅由圆圈和线条组成,分别代表陆地和桥梁。
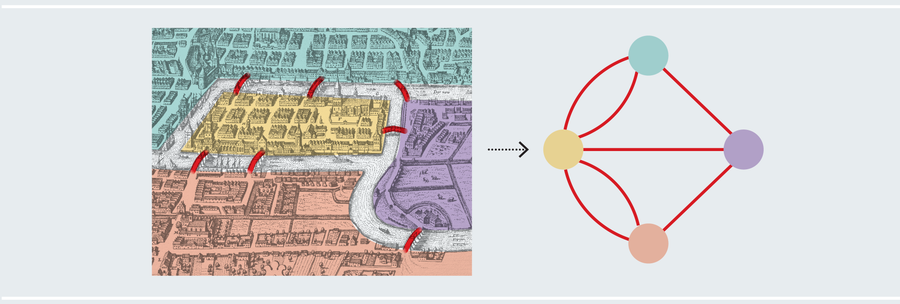
图片来源:Alamy Stock Photo(地图);阿曼达·蒙塔内斯(突出显示和图表)
现代数学术语称之为“图”,不要与其他不相关的数学图(如 x-y 平面中的绘图或统计可视化(如条形图))混淆。或许“网络”会是一个更好的术语,以避免任何混淆。我们称圆圈为“顶点”,线条为“边”。如今,图论是数学和计算机科学的一个主要领域,应用范围广泛。图不必代表陆地和桥梁。它们可以代表社交网络、蛋白质相互作用、州界、神经网络、万维网或任何其他涉及成对关系的数据。
抽象使数学家能够将一个关于旧城市特定桥梁排列的高度具体问题转化为关于所有图的一般问题。给定一个具有任意数量顶点和边的图,是否存在一条恰好遍历每条边的路径?事实证明,一个非常简单的测试可以回答任何图的这个问题:对于每个顶点(我们当前难题中的陆地),计算从它发出的边的数量(桥梁)。如果所有这些计数都是偶数,或者如果除了两个之外的所有计数都是偶数,则路径存在;否则,路径是不可能的。
让我们探讨一下其中的道理。想象一条穿过图的路径,该路径恰好穿过每条边一次。考虑该路径中间的顶点(不是起点或终点顶点)。如果该顶点有很多边,那么您的路径将多次访问它,但是每次您进入顶点时,也必须通过不同的边退出它。因此,路径中间的顶点每次被访问时,两条边都会被访问。这只有在路径中间的每个顶点都有偶数条边的情况下才有效。路径的起点和终点是唯一的例外,因为起点不必进入,而终点不必退出。因此,如果我们恰好有两个具有奇数条边的顶点,那么如果您从这些顶点开始和结束,我们的路径是可能的。如果每个顶点都有偶数条边,那么将存在一条路径,该路径从同一顶点开始和结束,形成一个环路。
这个论证被认为是图论中的第一个成果,而穿过图并访问每条边一次的路径现在被称为欧拉路径。 从技术上讲,欧拉的论证仅描述了使欧拉路径不可能存在的条件,而在这些条件下欧拉路径始终存在的证明是后来才出现的。将我们所学到的知识应用于柯尼斯堡的桥梁,我们看到所有四个顶点都有奇数条边从它们发出,这意味着,唉,普鲁士的漫步者徒劳地寻找了。
这是一个奇特的旁注。找到一条穿过图并恰好访问每个顶点(我们示例中的陆地而不是桥梁)一次的路径,听起来像是一个密切相关的问题,但实际上是一个完全不同的难题。虽然一个简单的测试可以确定一个图是否包含欧拉路径,但我们不知道任何通用的高效程序来解决这个以顶点为中心的变体。这个变体被称为哈密顿路径问题,它属于一类被广泛认为计算上难以处理的问题。
尽管欧拉最初对桥梁问题嗤之以鼻,但他最终还是被他无法用他常用的工具包解决这个问题所吸引。他给一位朋友写信说:“这个问题是如此平庸,但在我看来值得关注,因为几何学、代数学,甚至计数的艺术都不足以解决它。” 当时,几何学关注的是距离、角度和面积等定量概念。但是,虽然桥梁问题在本质上似乎是几何的,但它并没有要求任何类型的测量。这个问题需要一种新的抽象,这种抽象忽略了传统的几何量,同时尊重了问题核心的成对连接。
将柯尼斯堡地图简化为一个简单的图的想法在事后看来似乎很明显,但许多最好的抽象都是如此。数学史讲述了抽象的力量。如果古代数学思想家有关于橙子、珍珠甚至地球的定量问题,他们可以开发定制的语言和技术来应对每个新的挑战。但是,一旦人们认识到这些看似不同的对象都实例化了相同的高阶实体:球体,这项工作就变得容易和清晰得多。给抽象一个名称和一个定义,就允许从未见过面的人们在彼此的工作基础上进行构建,而无需重新发明轮子。
欧拉的论文不仅开创了图论领域,而且还为另一个主要的数学分支奠定了基础,即拓扑学。拓扑学指的是研究几何性质,即使我们像对待由高弹性橡胶制成的物体一样拉伸、压缩或变形物体,这些几何性质仍然存在。因此,虽然一个层次的抽象将我们从现实世界的物体(如橙子、山脉和骰子)带到它们的形状(球体、金字塔和立方体),但拓扑学引入了第二个抽象层次,在这个层次中,我们将球体、金字塔和立方体视为某些甚至更高阶实体的实例化。拓扑学家认为这些固体是等价的,因为它们都可以在橡胶世界中被塑造成彼此,而不像甜甜圈,无论你如何拉伸它,甜甜圈都会保持一个孔。
通过抽象掉柯尼斯堡地图中的定量细节,欧拉为一种新的几何思维方式打开了大门,这种思维方式摆脱了千年来一直主导该学科的距离和角度的定量细节。图论和拓扑学今天继续产生新的数学见解,我们应该感谢逝去的漫步文明。