“请来一杯健力士!”一位顾客对酒保说,酒保拿起一个印有商标的品脱杯,放在龙头下接酒。酒保开始一个精确耗时 119.5 秒的多步骤倾倒过程,无论这是一种营销噱头还是酒精工程的奇迹,都已经成为全球酒吧里一种受人喜爱的仪式。结果:一杯浓郁的烈性黑啤酒,上面有一层完美的泡沫,就像一杯泥土味的奶昔。
自创始人亚瑟·健力士在都柏林签订了一份年租金 45 英镑的 9000 年租约以来,健力士啤酒厂就以其创新方法而闻名。例如,在经过四年的尝试后,一位从数学家转行为酿酒师的迈克尔·爱德华·阿什发明了一种化学技术,使该啤酒厂的同名烈性黑啤酒具有天鹅绒般的泡沫。该方法包括向啤酒桶和健力士罐内的小球中添加氮气,催生了当今非常流行的“氮气冷萃”啤酒和咖啡风格。
但到目前为止,这家啤酒厂最具影响力的创新与啤酒无关。它是 t 检验的诞生地,t 检验是所有科学领域最重要的 统计技术 之一。当科学家宣布他们的发现“具有统计显著性”时,t 检验通常是这一结论的基础。这是如何运作的?为什么它会起源于啤酒酿造这种行业呢?
关于支持科学新闻业
如果您喜欢这篇文章,请考虑支持我们屡获殊荣的新闻业,方式是 订阅。通过购买订阅,您将帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事能够持续下去。
在 20 世纪初,健力士啤酒厂已经运营了近 150 年,并作为世界上最大的啤酒厂傲视群雄。在此之前,其产品的质量控制包括粗略的目测和气味测试。但是,全球扩张的需求促使健力士的领导者改进他们的方法,以实现目标一致性和工业级严谨性。该公司聘请了一支智囊团,并赋予他们自由,让他们可以为了酿造完美的啤酒而追求研究问题。这家啤酒厂成为实验中心,以解答一系列问题:哪里生长的大麦品种最好?麦芽提取物中理想的糖含量是多少?最新的广告宣传活动增加了多少销量?
Shuyao Xiao
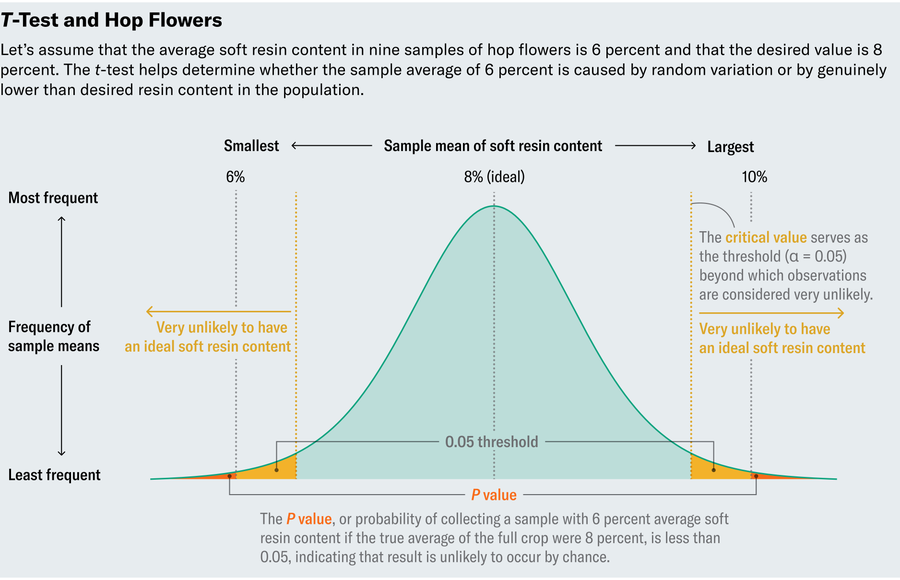
在蓬勃发展的科学活力中,该团队面临着一个持续存在的问题:如何在小样本量的情况下解读其数据。酿酒师面临的一个挑战涉及啤酒花,啤酒花是健力士啤酒的重要成分,它赋予啤酒苦味并充当天然防腐剂。为了评估啤酒花的质量,酿酒师测量植物的软树脂含量。假设他们认为 8% 是一个良好且典型的数值。但是,测试作物中的每一朵啤酒花在经济上是不可行的。因此,他们做了任何优秀的科学家都会做的事情,并测试了啤酒花的随机样本。
让我们检查一个虚构的例子。假设我们测量了九个样本的软树脂含量,并且由于样本各不相同,观察到值的范围从 4% 到 10% 不等,平均值为 6%——太低了。这是否意味着我们应该倾倒这批作物?不确定性来自对低值的两种可能解释。要么这批作物的软树脂含量确实异常低,要么即使样本包含的量很低,但整个作物实际上很好。抽取随机样本的全部意义在于依靠它们作为整个作物的忠实代表,但也许我们很不幸地选择了具有异常低水平的样本。(毕竟我们只测试了九个样本。)换句话说,我们应该认为样本中的低树脂含量与 8% 显着不同,还是仅仅是自然的变异?
这个问题并非啤酒酿造独有。相反,它渗透到所有科学探究中。假设在医学试验中,治疗组和安慰剂组都有改善,但治疗组的效果略好。这是否为推荐测试药物提供了充分的理由?如果我告诉你这两个组接受了两种不同的安慰剂呢?您是否会倾向于得出结论,认为给予结果较好组的安慰剂一定具有药用特性?或者可能是,当您跟踪一群人时,他们中的一些人自然会好转,有时会好转一点,有时会好转很多?同样,这归结为一个 统计显著性 问题。
Shuyao Xiao
在健力士啤酒厂出现之前,特别是直到 20 世纪初健力士啤酒厂的首席实验酿酒师威廉·西利·戈塞特发明了 t 检验,关于小 样本量 领域中这些长期存在的问题的理论才得以发展。统计显著性的概念早于戈塞特,但之前的统计学家是在大样本量的情况下工作的。要理解为什么这种区别很重要,我们需要了解如何确定统计显著性。
请记住,在我们的假设场景中,啤酒花样本的平均软树脂含量为 6%,我们想知道整个作物的平均值实际上是否与期望的 8% 不同,或者我们只是样本运气不好。因此,我们将问一个问题:如果整个作物是典型的(平均值为 8%),那么我们观察到如此极端值(6%)的 概率 是多少?传统上,如果这个概率(称为 P 值)小于 5% 或 0.05,那么我们就认为这种偏差具有统计显著性,尽管不同的应用需要不同的阈值。
通常,两个独立的因素会影响 P 值:样本偏离总体预期值的程度以及大偏差的常见程度。可以将其视为信号与噪声之间的拉锯战。我们观察到的均值(6%)与我们期望的均值(8%)之间的差异提供了信号——这种差异越大,作物真正具有低软树脂含量的可能性就越大。花朵之间的标准差带来了噪声。标准差衡量数据在均值周围的离散程度;小值表示数据在均值附近波动,而大值表示更大的变异。如果软树脂含量通常在芽之间波动很大(也就是说,如果它具有较高的标准差),那么也许我们样本中的 6% 平均值不应该让我们担心。但是,如果花朵倾向于表现出一致性(或较低的标准差),那么 6% 可能表明与期望的 8% 存在真正的偏差。
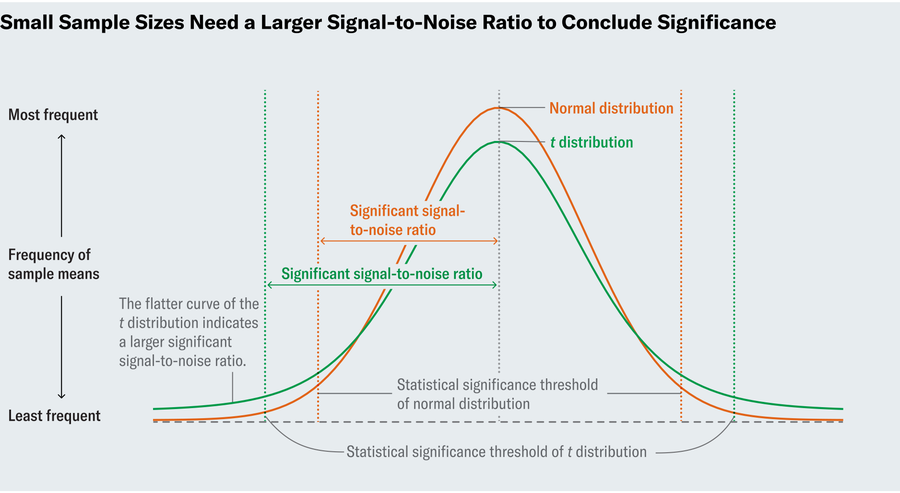
为了在理想世界中确定 P 值,我们将首先计算信噪比。该比率越高,我们对研究结果的显著性就越有信心,因为高比率表明我们发现了真正的偏差。但是,什么才算是高信噪比呢?为了认为 6% 与 8% 显着不同,我们特别想知道信噪比何时如此之高,以至于在树脂含量为 8% 是常态的世界中,只有 5% 的可能性发生这种情况。戈塞特时代的统计学家知道,如果您多次运行实验,计算每次实验中的信噪比并绘制结果图,则该图将类似于“标准正态分布”——熟悉的正态分布曲线。由于正态分布是众所周知的且有充分记录的,因此您可以在表格中查找比率必须有多大才能达到 5% 的阈值(或任何其他阈值)。
戈塞特认识到,这种方法仅适用于大样本量;小啤酒花样本不能保证正态分布。因此,他一丝不苟地为较小的样本量制表了新的分布。现在称为 t 分布,这些图类似于正态分布,因为它们是钟形的,但钟形曲线的下降程度不如正态分布那么剧烈。这意味着需要更大的信噪比才能得出显著性结论。他的 t 检验使我们能够在以前人们无法进行推断的情况下进行推断。
2008 年,数学顾问约翰·D·库克在他的 博客 中思考,也许 t 检验起源于啤酒厂而不是葡萄酒厂不应该让我们感到惊讶。啤酒厂要求其产品的质量保持一致,而酿酒师则陶醉于多样性。葡萄酒有“好年份”,每瓶酒都有一个故事,但您希望每一杯健力士啤酒都能提供相同的标志性口味。在这种情况下,统一性激发了创新。
戈塞特用他的新技术解决了啤酒厂的许多问题。这位自学成才的统计学家以笔名“Student”发表了他的 t 检验,因为健力士不想向竞争对手泄露其研究成果。尽管戈塞特开创了工业质量控制,并为定量研究贡献了大量其他想法,但大多数教科书仍然称他的伟大成就为“Student’s t-test”(学生 t 检验)。历史可能忽略了他的名字,但他可以自豪的是,t 检验是迄今为止科学界最广泛使用的统计工具之一。也许他的成就应该被载入《吉尼斯世界纪录大全》(这个想法是健力士啤酒厂的总经理在 20 世纪 50 年代构想出来的)。为此干杯。
