在明星云集的悬疑惊悚片《灵数23》于2007年在电影院上映后,许多人开始确信他们在任何地方都能看到这个同名数字。那时我还在上学,我的一些同学每当数字23出现在任何语境中都会不寒而栗。其他人则对这种形式的命理学着迷,因为一旦你更多地关注某个事物——包括一个数字——你就会感觉你看到它的频率太高了,不可能是纯粹的巧合。
长期以来,人们一直认为已故数学家约翰·麦凯可能也成为了这种被称为“频率错觉”或巴德尔-迈因霍夫现象的受害者。在麦凯的案例中,抓住他想象力的数字是196,884。
像23这样的两位数反复出现似乎并不太令人惊讶。但是一个六位数的数字也会这样做吗?麦凯在1978年偶然发现了这个数字,当时他正在翻阅一篇数学领域的论文,而这个领域并不是他的专长。他研究的是几何学,研究的是图形的对称性。然而,那天,他正在查看来自数论的结果,数论是研究整数的性质的,例如素数。他偶然发现了一个以值196,884开头的数字序列。
支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们今天世界的发现和想法的具有影响力的故事。
这个数字听起来麦凯很熟悉。他之前研究过一种数学结构——当时仍然是假设性的——被称为“怪兽”。这种奇怪的代数结构旨在描述一个生活在196,883维空间(仅比数字196,884少一维)中的几何物体的对称性。而且由于一维点无论如何都满足每个对称性,因此怪兽也可以描述其对称性质。因此,麦凯以一种非凡的方式再次发现了数字196,884。他将数学家认为怪兽对称性适用的前两个维度相加:196,883 + 1 = 196,884。
这听起来牵强附会吗?其他人也这么认为。专家们对麦凯的结果几乎没有关注。毕竟,像怪兽这样的结构包含许多数字,麦凯与之相关的数论结果也是如此。“如果你有很多数字,那么其中一些数字会大致相同,这只是巧合,”数学家理查德·博切兹说,他在该领域做出了重大贡献,在一个解释性的YouTube视频中。
但是麦凯无法摆脱几何学和数论这两个截然不同的数学领域可能存在联系的感觉。据报道,他甚至在会议上穿着印有“196,883 + 1 = 196,884”字样的T恤。
完全疯狂还是天才之举?
不久之后,数学家约翰·汤普森意识到麦凯的怀疑可能并非毫无道理。他成功地将物体遵循怪兽对称性的下一个更高维度与数论中神秘数字序列的下一个成员联系起来。维度是21,296,876。这些值有所不同——但是如果你像以前一样将所有怪兽维度加起来(1 + 196,883 + 21,296,876),结果是21,493,760。
这令人惊讶,因为你可能还记得,当麦凯第一次发现196,884时,他正在查看数论中的一个特殊序列。该序列中的第二个数字是21,493,760——汤普森的结果。换句话说,看起来两个看似无关的数学领域之间真的可能存在联系。
此时,数学界开始感到好奇。也许麦凯毕竟是对的——即使这听起来完全荒谬。这种描述难以想象的物体的对称性并且甚至尚未完全构建的奇怪结构,与数论有什么关系呢?
到1979年,越来越多的证据表明,其他数字和维度似乎也遵循这种出乎意料的模式。数学家约翰·康威和西蒙·诺顿最终发表了一篇题为“怪兽月光”的论文,其中他们提出了几何学和数论之间存在联系的猜想。“他们称之为月光,因为它看起来太牵强了,”德国波恩马克斯·普朗克数学研究所的数论家唐·扎吉尔在2015年对Quanta Magazine说。
事实上,证明这个月光猜想可能几乎没有希望。除了这两个遥远的数学领域是否有关联尚不清楚之外,甚至怪兽是否真的存在也完全不清楚。
月光下的怪兽
怪兽是群论的理论预测,群论是几何学的一个分支,处理物体的对称性质。在20世纪70年代,数学家开始创建一种群的元素周期表:他们想找到有限对称性的“原子”。根据这种思维方式,每个有限群都可以用这些原子的组合来表示。经过数十年的研究,几何学家似乎终于达到了他们的目标。与化学元素不同,存在无限多的“有限单群”,但几乎所有群都可以分为18类,其排列方式让人联想到元素周期表。此外,专家们总共发现了26个不属于这18类的外来者。
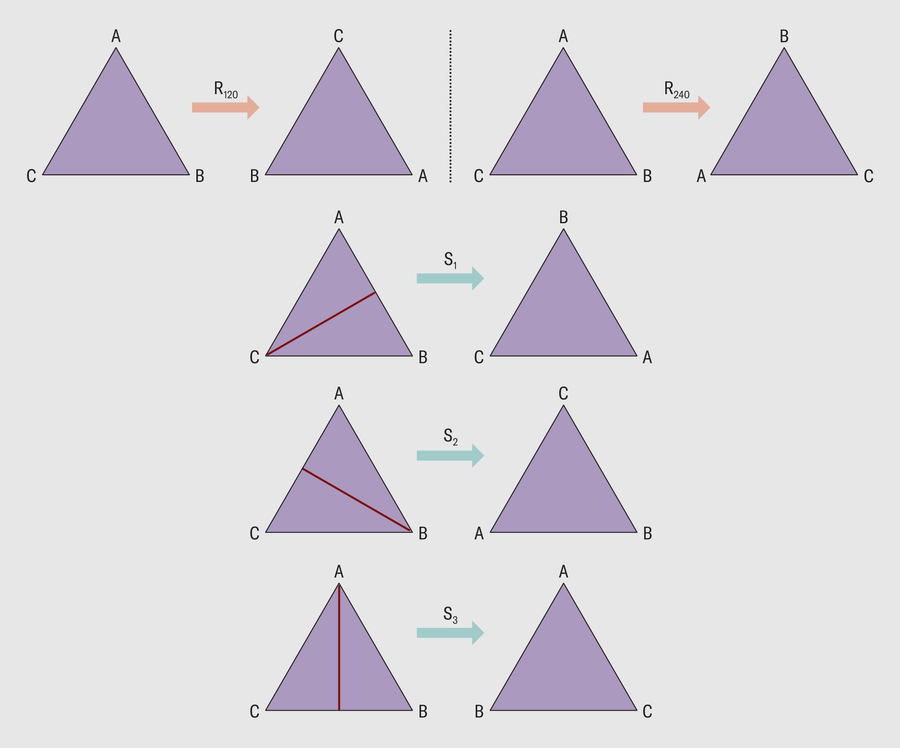
三角形的对称性形成一个有限群。图片来源:Spektrum der Wissenschaft/马农·比肖夫,阿曼达·蒙塔内斯重新设计
这些离群值中的第一个是“怪兽”,数学家伯恩德·费舍尔和罗伯特·格里斯在1973年预测了它。这个名字来源于这个群的庞大规模:它包含超过8 x 1053个对称性。作为比较,一个20面“D20”骰子(一个二十面体)的对称群包含60个对称性,这意味着可以进行60种可能的变换(旋转或反射)而不会改变D20的方向。
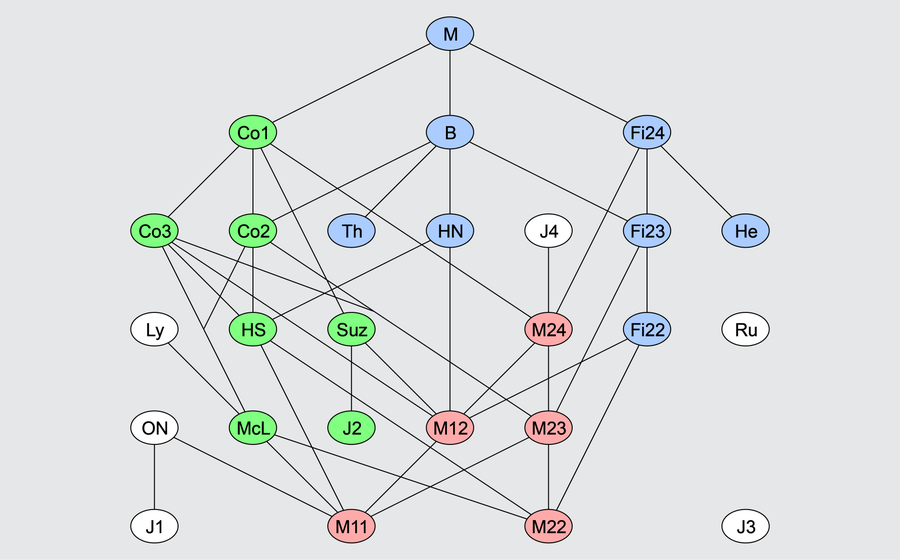
一些红色、绿色和蓝色的零星群彼此相关。白色的零星群被认为是外来者。图片来源:Drschawrz/Wikimedia Commons(CC BY-SA 3.0)
由于其庞大的规模,怪兽给数学家带来了巨大的挑战。“大多数人认为构建它将是毫无希望的,因为当时即使是小得多的群也需要计算机构建,”博切兹在他的YouTube视频中解释道。与此同时,即使是功能强大的计算机也难以处理由8 x 1053个元素组成的结构。
然而,这种悲观的预测最终被证明是错误的。1980年,格里斯构建了怪兽,从而证明了它的存在——没有借助计算机的帮助。
类固醇上的正弦函数
数论主要研究整数,乍一看似乎很简单。但是为了研究它们之间的关系,专家们求助于复杂的概念,例如所谓的模形式。这些是函数f(z),它们非常对称。与正弦函数一样,你只需要知道模形式的特定部分就可以知道它在其他任何地方的样子。
“模形式有点像三角函数,但加了类固醇,”数学家肯·小野告诉QuantaMagazine。
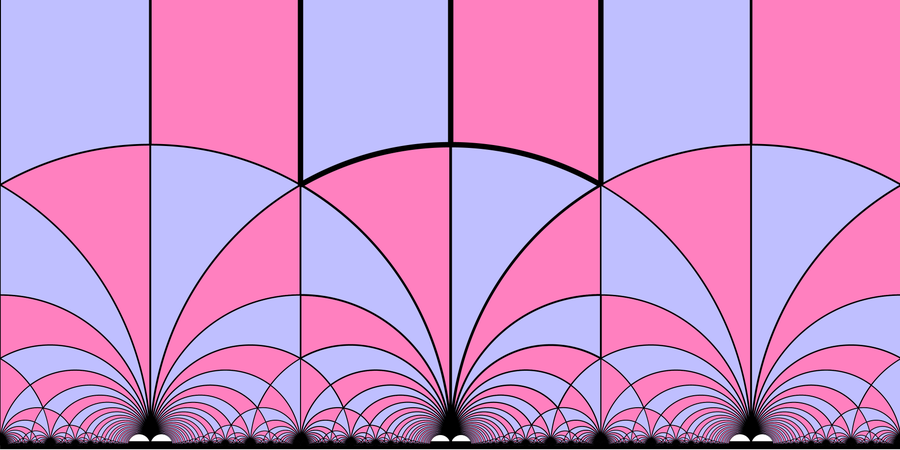
彩色模形式包括模空间,如图所示,模空间是一个几何空间,其点对应于固定的代数几何对象。图片来源:Neozhaoliang/Wikimedia Commons(CC BY-SA 4.0)
尽管如此,它们在数学中起着极其重要的作用。例如,牛津大学的安德鲁·怀尔斯使用它们来证明费马大定理,而瑞士洛桑联邦理工学院的玛丽娜·维亚佐夫斯卡使用它们来寻找八个空间维度中最密集的球体堆积排列。然而,由于模形式非常复杂,它们通常用无限长的多项式来近似,例如
f(q) = (1⁄q) + 744 + 19,688q + 21,493,760q2 + 864,299,970q3 + …
变量q前面的前因子形成一个从数论角度来看具有有趣性质的数字序列。麦凯将这个数字序列与怪兽联系起来。
一个令人惊讶的联系
博切兹在20世纪80年代首次听说了月光猜想。“我当时完全被它震惊了,”他在接受YouTuber Curt Jaimungal的采访时回忆道。博切兹当时正在康威的一次讲座中,了解到数论和群论可能存在神秘的联系。这个主题从未让他释怀。他开始寻找可疑的联系,直到他找到了它。1992年,他发表了他的突破性成果,并因此在六年后的1998年获得了菲尔兹奖,这是数学领域的最高奖项之一。他的结论是:一个高度投机的物理学领域,弦理论,可以为怪兽和数字序列之间缺失的拼图提供答案。
弦理论试图统一物理学的四种基本力(电磁力、强核力、弱核力和引力)。与传统理论中依赖粒子或波来构成宇宙的基本组成部分不同,弦理论涉及一维结构:微小的线状物像乐器的弦一样振动,从而产生我们在宇宙中感知到的熟悉的粒子和相互作用。
博切兹知道弦理论是基于许多与对称性相关的数学原理的。事实证明,模量也起着作用。当微小的线状物闭合并在时空中以摆动的方式移动时,它们的轨迹形成一个二维管。无论线状物如何振荡,这种结构都具有与模形式相同的对称性。
博切兹研究的那种弦理论只能在25个空间维度中进行数学公式化。然而,由于我们的世界仅由三个可见的空间维度组成,因此弦理论家假设其余22个维度卷曲成微小的球体或甜甜圈状的环面。但是物理学取决于它们的精确形状:维度卷曲成圆柱体的弦理论提供的预测与维度形成球体的弦理论提供的预测不同。为了以适合我们世界的方式描述粒子及其相互作用,物理学家必须在他们的计算中找到正确的“紧致化”。
博切兹将24个维度卷曲成一个24维的甜甜圈表面,并发现相关的弦理论具有怪兽的对称性。只剩下一个自由空间维度并没有困扰他。毕竟,他对模型的数学性质感兴趣,而不是对描述我们世界的物理理论感兴趣。
在这个构建的世界中,线状物沿着24维的甜甜圈摆动。怪兽的维度计算了线状物在特定能量下可以振动的所有方式。因此,在最低能量下,它仅以一种方式振动;在下一个最高能量下,已经有196,883种不同的可能性。并且线状物留下的轨迹具有模形式的对称性。
博切兹因此证明了怪兽群和模形式之间的联系。而且这不会是唯一的这种情况:与此同时,数学家们已经能够将其他有限群与其他模形式联系起来——在那里,弦理论也提供了联系。因此,即使事实证明这种投机理论不适合描述我们的宇宙,它仍然可以帮助我们发现全新的数学世界。
本文最初发表于Spektrum der Wissenschaft,经许可转载。
