Benjamin Adric Dunn,挪威科技大学的数据科学家,向我展示了一张排列不均匀的点图,模糊地像巨石阵的岩石。 总体模式很清晰——至少对人类来说是这样。“当我们看这个时,很明显这是一个圆圈,”他说。 但算法很可能难以识别这个简单的形状。“它经常忽略大局。”
许多科学过程都涉及循环或重复。 计算机无法看到这些关系对于想要在大量数据点中识别循环模式的科学家来说是一个问题。 数据通常被可视化为漂浮在空间中的点,就像夜空中的星星一样。 一个点可能代表一个物理位置,例如标记船舶在公海位置的经度和纬度两个数字。 基因同样可以绘制在许多维度的数学空间中——有时是数百个维度——这样,具有相似 DNA 序列的两个基因将由附近的点表示。 数据中循环模式的意义取决于上下文。 船舶位置中的圆圈可能表明它迷路了,而遗传数据中的圆圈可能证明进化关系。
通常,这些数据点的星空过于复杂和高维,无法用肉眼研究。 为了检测圆圈,研究人员需要一套足够精确的指令,以便计算机能够理解。 但是,许多标准的数据分析技术都基于一种称为线性代数的数学类型,它研究直线和平坦平面。 为了找出循环,研究人员转而使用拓扑数据分析 (TDA),这提供了一种完全不同的视角。
与表征线性代数的相对简单和刚性的结构相比,TDA 以拓扑学为基础,拓扑学是数学的一个分支,研究柔韧的、可拉伸的形状。 因为它的从业者假设所有形状都是任意灵活的,所以拓扑学通常被称为橡皮泥几何学。
就像从星星形成星座一样,拓扑数据分析帮助数学家从分散的点构建揭示性的形状。 研究人员首先将数据点用作虚拟支架中的节点或关节,构建可能延伸到数百维度的复杂结构。 由此产生的图片包含原始数据的大部分本质,但以更具体的形式呈现。 他们使用拓扑视角研究这些结构——寻找即使支架被拉伸或弯曲也能保留的特征。
拓扑学在数据分析中的用处在于它能够揭示定性而非定量的属性。 它识别结构的各个方面,即使在底层测量中存在随机误差或噪声,这些方面仍然存在。 噪声通常会抖动底层数据,但拓扑结构保持不变——揭示系统的稳健特征。“在现实世界中,有很多实例给你的数据是软绵绵的,”宾夕法尼亚大学的数学家罗伯特·格里斯特说。“所以你必须使用软绵绵的数学。”
数学家和科学家现在正在共同努力,在大量数据中寻找不寻常的拓扑形状,这些数据代表从具有日常节律的生物过程到药物分子的结构等任何事物。 也许这些研究中最有趣的是关于大脑结构的。 数学家已经使用拓扑学来探索神经元如何在整个大脑的扩展区域相互作用,对不同的环境和刺激做出反应。 最近,邓恩与神经科学家合作发现,某些脑细胞使用环面(甜甜圈表面的数学名称)来绘制其环境图。

图片来源:Jen Christiansen
甜甜圈和咖啡杯
即使拓扑学家以扭曲橡皮泥为生,他们也非常小心地保持其中的孔洞数量。 他们从不打出新孔或压闭现有孔。 有一个经典的数学笑话,拓扑学家无法区分甜甜圈和咖啡杯:它们都有一个孔。
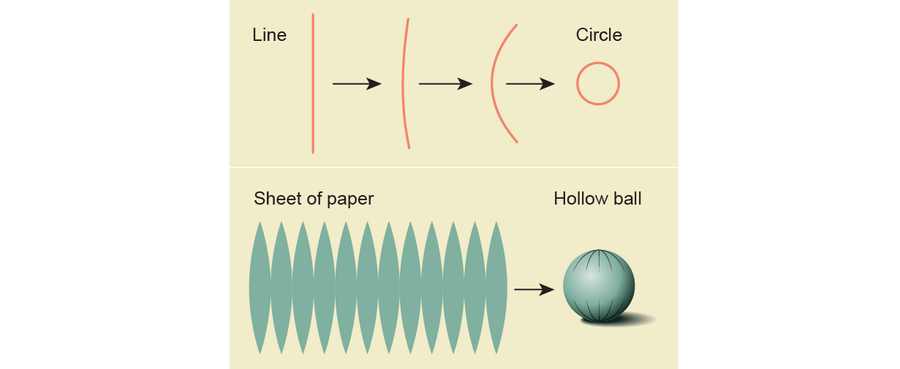
拓扑学家根据孔的维度对孔进行分类。 闭环,如数字 0,有一个一维孔,因为它是由将一维线的两端粘合在一起形成的。 从二维平面(如一张纸)开始,并粘起边缘将产生类似空心球的东西,它有一个二维孔。
图片来源:Jen Christiansen
更高维度的形状可以有更高维度的孔。 通过类比一维和二维孔,例如,三维孔是通过“封闭”三维空间(如立方体)形成的。 但是这个过程只能从四维视角来看,超出大多数人——可能任何人的——理解范围。
有些形状有多个不同维度的孔,例如带有附加把手的充气球,孩子可以坐在上面弹跳。 球的空心中心是一个二维孔,而实心把手形成一个一维孔。 拓扑学有许多精确的方法来计算更高维度形状中的孔洞——这种能力被证明有助于研究大脑的神经元活动。
印第安纳大学的神经科学家奥拉夫·斯波恩斯将大脑视为一个庞大的交通网络。 道路和基础设施由神经元及其连接的突触构成。 大脑的电信号和化学信号沿着这些街道驱动。“物理道路限制了你可以在顶层动态观察到的交通模式,”斯波恩斯说。 当我们移动和思考时,交通模式会发生变化。
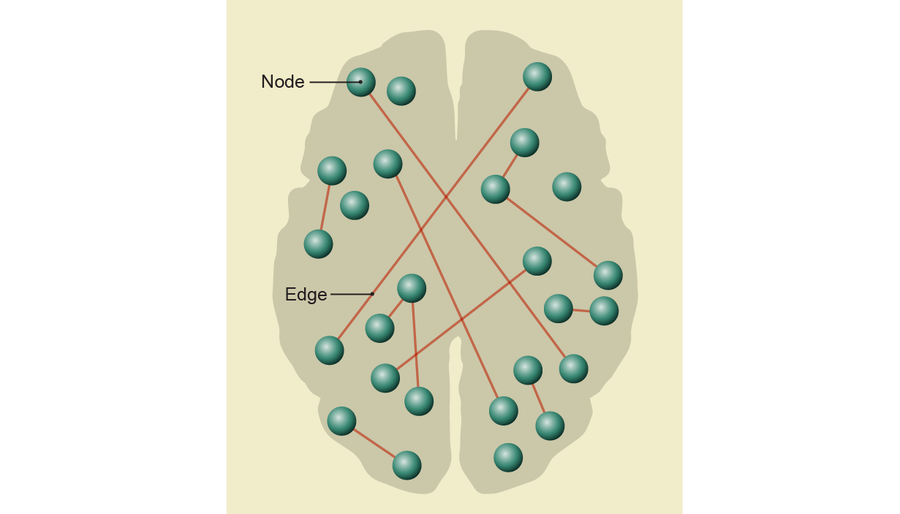
当我们眯着眼睛看大脑的图表时,它可能看起来像点的集合,代表神经元。 其中一些点由线条连接,表示这些特定神经元之间的突触。 数学家将这种结构称为图:由边连接的节点的集合。 图使大脑的生物复杂性变得扁平,但它保留了电路的整体形状。 这种权衡在创建数学模型时很典型,数学模型权衡简单性和可分析性与实用性。
图片来源:Jen Christiansen
神经元连接图是一个网状结构:神经元丰富且相互交织。 2017 年,洛桑瑞士联邦理工学院的数学家凯瑟琳·赫斯通过做一件最初令人惊讶的事情来解决这种复杂性:她使图变得更加复杂。 她分析了来自蓝脑计划的数据,这是一个大规模计算机模拟啮齿动物新皮层活动的项目,新皮层是大脑中参与高阶功能的部分。 该计算机模型包含单个神经元的表示,这些神经元通过突触连接到其他模拟神经元。 这些连接以及它们何时可能放电由基本的生物学原理和来自实验室啮齿动物的实验数据决定。
该模拟可以显示大脑的交通模式——神经元响应刺激而放电。 然而,与真实大脑的鸟瞰图不同,模拟可以暂停,让科学家看到冻结帧,显示哪些突触正在响应给定的刺激而放电。 将此静态图像转换为图很容易,因为它指示了数据点以及它们之间的线条:如果连接它们的突触正在放电,则两个神经元是连接的。 从这张图中,赫斯构建了数学家称之为单纯复形的东西,将简单的图转换为体积庞大的形状。
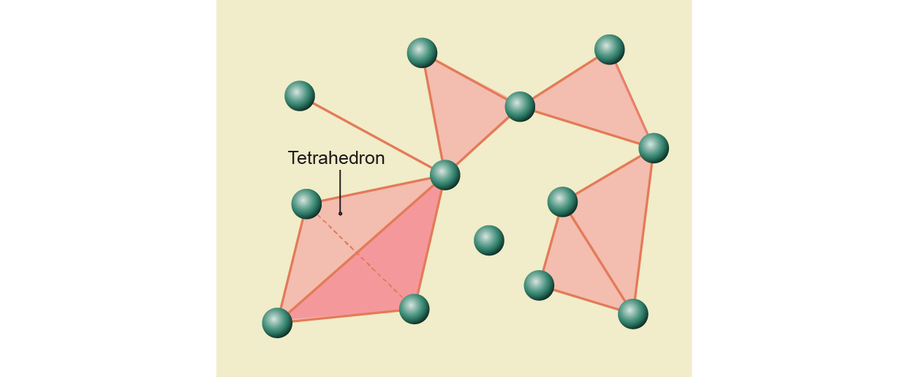
单纯复形由不同维度的三角形构成。 例如,在蓝脑图中,三个神经元,它们之间所有三个突触都传输信号,形成了空心三角形的顶点。 为了将这种结构扩展为单纯复形,数学家们用实心的二维三角形填充了这个空心三角形。 同样,他们用更高维度的三角形类似物填充了更大的连接神经元簇。 例如,四面体(一个带有四个三角形面的实心三维金字塔)将填充一组四个同时放电的神经元。
赫斯和其他人观察到的作为一组放电的神经元的最大数量是八个,因此这个单纯复形的最大部分是一个七维三角形。 许多元素重叠,形成一个多维雕塑:一个三角形可能从四面体中突出,并在一个点与另一个三角形相遇。 此外,数学家和科学家不仅检查了一个,而且检查了一系列冻结帧,这些帧是在模拟轻轻抚摸啮齿动物的胡须后拍摄的。 他们将这些地图中的每一个都转换为一个单纯复形,并使用拓扑学工具分析其形状如何随时间变化。
图片来源:Jen Christiansen
在接收到刺激后,单纯复形立即像一个巨大的乐高积木结构一样增长,添加更高维度的碎片,直到雕塑达到最大三维或四维,具体取决于刺激。 然后整个东西迅速消失。“你有这些越来越复杂的结构,它们是由刺激创建的,直到它完全崩溃,”赫斯说。
对于拓扑学家来说,连接成三角形的三条线与空心圆相同,因为一种形状可以弯曲成另一种形状。 因为赫斯和她的同事从模拟啮齿动物大脑构建的单纯复形是七维的,所以它们可以有多达七个维度的孔。 他们的分析表明,随着形状的增长,孔的数量也在增加。 在其峰值时,该结构包含惊人数量的二维和三维孔——比随机单纯复形或从不同生物过程构建的单纯复形产生的孔多得多。 孔的特定模式揭示了神经元反应的高度组织性;这种复杂性可能表明思维过程的基本特征。
顽固的孔
然而,更常见的情况是,数据由漂浮在抽象数学空间中的孤立点表示,没有明显的、预先确定的连接。 为了应用 TDA,数学家需要弄清楚如何连接它们。 但是有很多可能的方式将星星连接成星座。 为了找到这些隐含的图画,数学家使用一种称为持久同调的技术。 拓扑学家分析以各种尺度构建的一系列单纯复形,以找到数据云的基本特征。
为了制作第一个单纯复形,他们尽可能广泛地撒网,将每个点连接到每个其他点以形成密集的网格。 用固体形式填充这个网络会产生一个高维单纯复形,几乎没有明显的特征。 但是数学家需要将这个复形与通过在较小尺度连接数据而形成的其他复形进行比较。 因此,接下来,他们在相同的数据上撒下更窄的网,仅连接附近的点。 现在他们有了一个更稀疏的网络,他们用它来构建第二个单纯复形。 因为这个网格包含的数据点较少,所以它的单纯复形包含较低维度的形状。 研究人员使用一系列更小的网重复该过程。“在每个尺度上,你都会得到该复形外观的不同快照,”俄亥俄州立大学的数学家兰索尼·埃德蒙兹说。
每个单纯复形都是用相同的分散数据点形成的可能星座。 拓扑学家研究这种形状谱——特别是记录每个维度中孔的数量。 他们对在许多不同尺度上持续存在的孔特别感兴趣。 有些孔短暂出现然后消失,但顽固的孔——那些在一定尺度范围内幸存下来的孔——指向数据的最基本特征。 因此,TDA 可以将复杂的数据混乱简化为顽固孔的简单列表,这与 JPEG 照片文件压缩图像的方式非常相似。“这是一种将数据精简为真正重要的东西的方式,以便我们拥有更实用的东西,”格里斯特说。
有时,以这种方式识别的孔具有直接的解释。 东北大学的数学家何塞·佩雷亚和一组计算生物学家使用持久同调来寻找周期性生物过程——那些以有规律的间隔重复的过程。 例子包括酵母的代谢周期或小鼠的昼夜节律。“什么是复发或重复?”佩雷亚问道。“从几何角度来看,它应该像你在你正在观察的事物的空间中遍历某种循环。”
TDA 还帮助研究人员设计新药。 这些化合物通常是通过调整现有药物的分子结构来发现的。 但是分子的结构极其复杂且难以分析,即使对于机器学习算法也是如此。 为了设计新药,计算机需要使用现有分子的简化表示。 有许多方法可以做到这一点,但密歇根州立大学的魏国伟领导的团队选择将分子简化为它们的“拓扑签名”。 这是基于其拓扑特征对化学物质的描述——本质上是通过持久同调获得的信息集合,例如每个维度中顽固孔的数量。
大脑循环
TDA 最有趣的应用可能是在大脑组织的最基本层面——单一类型的神经元。 2014 年,约翰·奥基夫和研究伙伴梅-布里特·莫泽和爱德华·莫泽因发现位置细胞和网格细胞(分别是在动物位于特定位置时激活的神经元类型)而获得诺贝尔医学奖。 宾夕法尼亚州立大学的数学家卡琳娜·库尔托说,它们充当位置传感器。
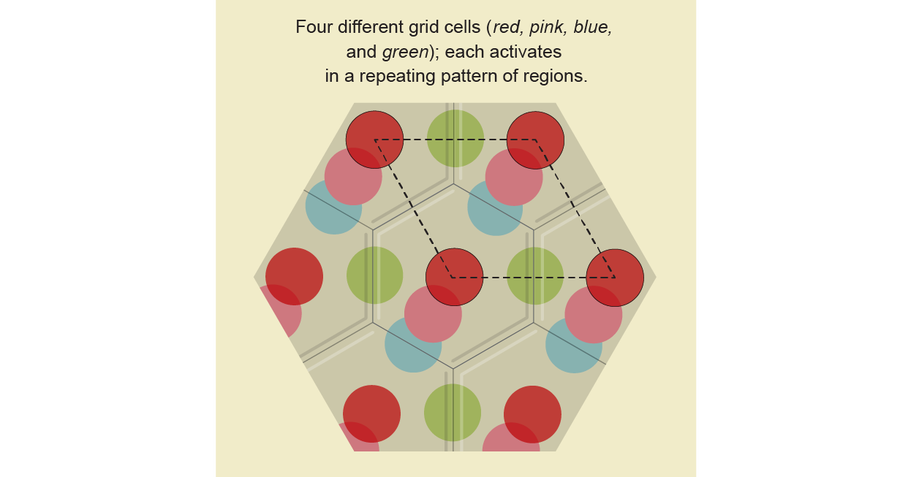
当大鼠在其环境中的多个位置时,其大脑中的每个网格细胞都会亮起。 为了弄清楚网格细胞与大鼠位置之间的关系,神经科学家选择了一个网格细胞进行研究。 他们在地板的计算机模型上画了一个点,标记大鼠每次激活该细胞的位置。 随着大鼠在方形盒子中自由移动,出现了一种规则且重复的点模式,数学家将其描述为六边形晶格。 晶格上的点代表该特定网格细胞亮起的所有位置。 他们对多个网格细胞重复了这个过程,用不同的颜色标记每个网格细胞。 与每个网格细胞对应的点具有相同的整体几何图案,但彼此偏移,像繁忙的瓷砖一样覆盖盒子。
图片来源:Jen Christiansen;来源:Carina Curto 在《美国数学会通报》第 54 卷第 1 期中发表的“拓扑学能告诉我们关于神经代码什么?”;2017 年 1 月(参考文献)
神经科学家想准确了解网格细胞如何表示空间位置——本质上,他们正在寻找产生六边形图案的模板。 例如,想象一个圆形橡皮图章,上面印有各种卡通人物。 当您展开图章时,它将创建一条线。 米老鼠的图像将沿线以规则的间隔出现。 但所有这些图像都来自原始橡皮图章上的同一位置。 很容易想象展开图章,但反向问题更具挑战性:如何从它创建的图案中生成模板图章?
在代表每个网格细胞放电时大鼠所在位置的彩色点平铺中,四个相邻的红点形成了倾斜矩形的角,该矩形称为平行四边形。 就像重复的米老鼠图像一样,所有相同颜色的红点都对应于单个网格细胞。 因此,拓扑学家识别出所有红点,使用他们称为“粘合”的操作将平行四边形折叠成甜甜圈形状。 首先,他们将平行四边形的两条相对边粘合在一起,形成一个带有两个红点的圆柱体:一个在顶部,一个在底部。 接下来,他们弯曲圆柱体,将两端粘合在一起形成环面。 这样,平行四边形的四个红色角就变成了甜甜圈上的一个点。 每种其他颜色的点正好会在环面上显示一个。 因此,就像圆形图章是卡通线条的模板一样,环面是网格细胞如何表示盒子地板的正确地图。
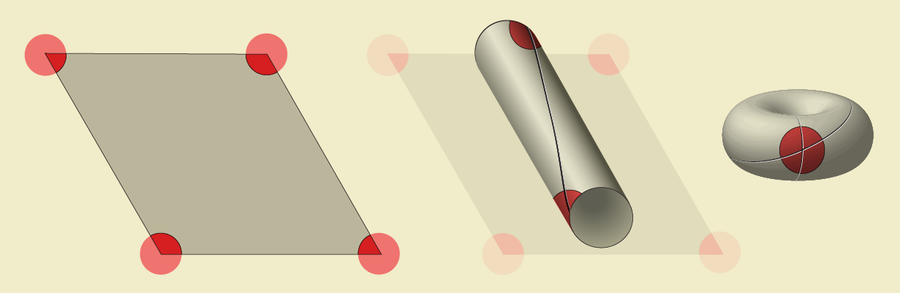
图片来源:Jen Christiansen
当大鼠在盒子周围跑动时,神经科学家可以看到这种模式。 但是,当大鼠在其他测试场地(例如带有轮辐和中心轮毂的自行车轮)周围移动时,更难以可视化该模式。 每个网格细胞仍然在多个位置放电,但科学家对底层地图没有信心。 点的排列结构不明显。
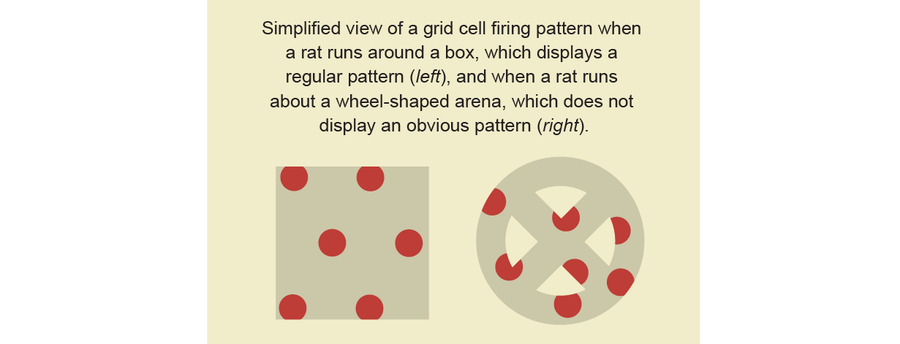
图片来源:Jen Christiansen
在 2022 年 2 月的 Nature 论文中,包括邓恩在内的一个数学家和神经科学家团队使用网格细胞来测试一种称为连续吸引子网络的理论,该理论预测某些神经元以特定模式连接在一起——即使动物处于不同情况下,该模式也不会改变。 为了测试连续吸引子网络理论,研究人员需要确定网格细胞是否总是形成环面,无论大鼠发现自己处于何种环境中。 他们在杂乱的神经学数据中搜索环面——这是 TDA 的完美工作。
这一次,研究人员没有标记单个网格细胞放电的盒子中的位置,而是研究了整个网格细胞网络的集体活动。 他们定期使用一串 0 和 1 记录网络的状态,这表示每个网格细胞是否处于活动状态。 从数学家的角度来看,这个长字符串是高维空间中的一个点。 实际上,当研究人员记录系统在不同时刻的状态时,他们正在积累高维数据点。 这些点描述了网格细胞激活模式随时间演变的方式,但数据太复杂,无法用肉眼研究。
在使用一些标准技术简化数据后,该团队通过在不同尺度上连接数据点并检查由此产生的单纯复形,计算了系统的持久同调。 和以前一样,当大鼠在盒子周围跑动时,数据形成了一个环面。 但真正的考验是研究人员从在轮状竞技场周围跑动的大鼠那里获得数据时。 令他们高兴的是,它再次形成了一个环面。
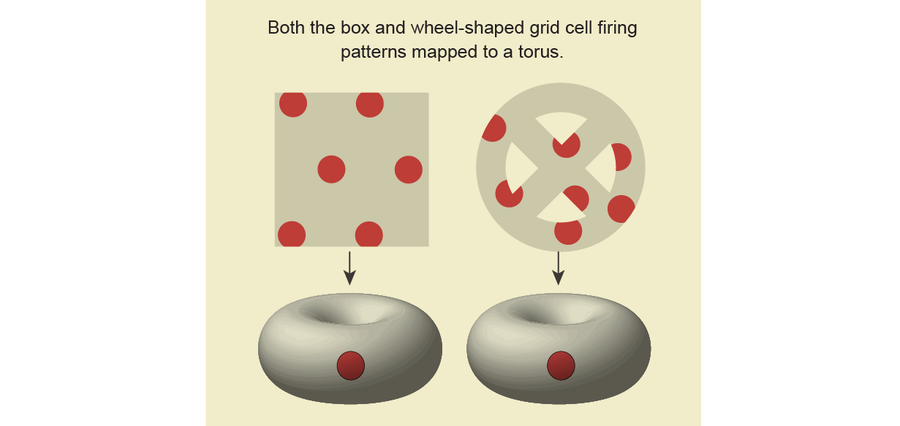
图片来源:Jen Christiansen
研究人员甚至能够从一只正在睡觉——可能正在做梦——的大鼠那里收集数据。 同样,他们发现了一个环面,无论大鼠的环境或存在状态如何,形状都持续存在,这一发现支持了连续吸引子网络理论。 甜甜圈形状似乎是网格细胞如何表示空间的内在特性。
拓扑数据分析的许多这些应用只有在强大的新型计算工具的支持下才有可能实现。“如果人们没有认真开始构建算法,这一切都不会发生,”牛津大学的数学家维迪特·南达说。“如果它不有效,如果它不能很好地扩展,那么无论理论多么美妙,都没有人想使用它。”
由于这些技术,拓扑学的用途正在蓬勃发展,直到最近,拓扑学似乎还只是一个抽象的、如果说有趣的话,数学分支。“应用越来越强大,”斯坦福大学数学家、TDA 的先驱之一贡纳尔·卡尔森说。“我们真的跨越了鸿沟。”

