2021 年,一对非传统的合作者开始了一项大胆的实验。数学家兼数理物理学家史蒂文·雷恩和自由作曲家、钢琴家兼长号演奏家杰夫·普雷斯拉夫花了两年时间准备回答一个大问题:他们能否将一篇数理物理研究论文直接翻译成音乐?更重要的是,他们的音乐创作会好听吗?
9 月,雷恩和普雷斯拉夫发布了他们的心血结晶,“数学 + 爵士:来自量子未来的声音。” 在萨斯喀彻温大学的研究员雷恩和居住在加拿大温尼伯的普雷斯拉夫首次通过电子邮件联系整整两年后的同一天,他们聚集了一个由 15 名音乐家组成的“双曲乐队”,在萨斯喀彻温大学表演了五部分的音乐会。每个部分都对应于雷恩的研究文章的一部分。
这场音乐会既是音乐表演,又是讲座,观众“座无虚席”,雷恩说。讲座部分剖析了论文的科学概念,并阐述了这些想法是如何转化为音乐的。一些插图是字面意义上的:幻灯片展示了艾略特·基恩泽创作的双曲艺术。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
举办这场音乐会绝非易事。雷恩指出,由于许多音乐家都不是本地人,乐队直到音乐会前一天晚上才在一起亲自排练音乐。
双曲能带理论
音乐基于雷恩 2021 年发表在《科学进展》(Science Advances) 上的文章《双曲能带理论》,这篇文章是他与阿尔伯塔大学的约瑟夫·马切伊科合著的。他们的目标是探索能带理论——研究人员用它来考虑材料的能级及其构成原子——是否可以被重新构建,以解释具有不规则、扭曲排列的双曲材料。
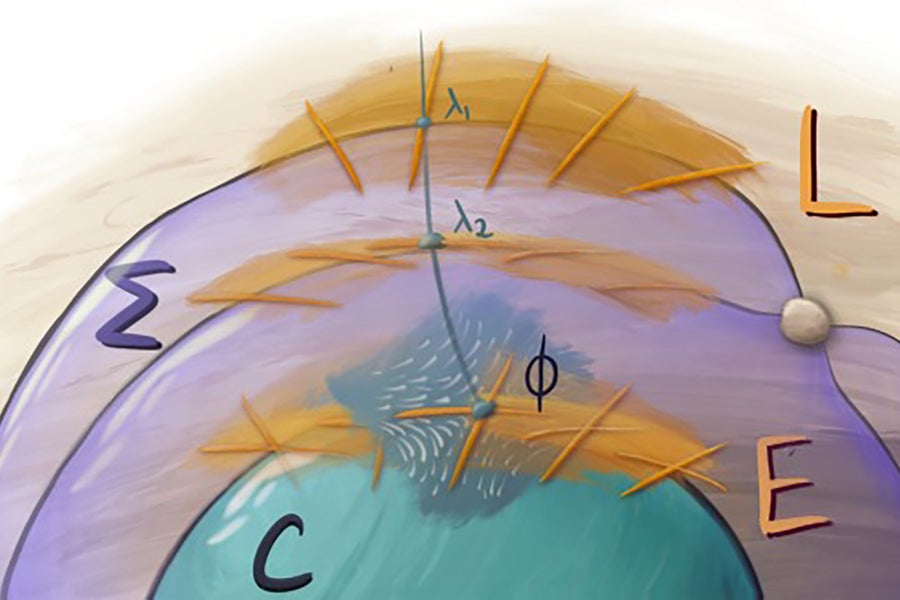
在能带理论中,材料的能级被认为包含在悬浮在它们所属材料上方的片状能带中。这些阴影能带代表了材料的量子特性,并且这些能带之间的相互作用对材料的行为有影响。
雷恩和马切伊科成功地发现了一种能带理论,该理论适用于怪异的双曲几何世界,这是一个打破欧几里得“平行公设”的奇怪几何领域。这条规则也称为欧几里得第五公设,它告诉我们以下内容:假设给定一条直线。对于任何不在该直线上的点,将只有一条直线既穿过该点又平行于原始直线。在双曲世界中,至少有两条直线将穿过该点,同时平行于给定的直线。
雷恩说,这项研究“是一种全新的材料设计方法——尤其是量子材料——通过从内到外重新设计它们的几何形状”。该方法涉及改变材料的能带结构,以在材料的性质中产生期望的变化。“它们可以呈现出不寻常的、奇异的几何形状,”他说。
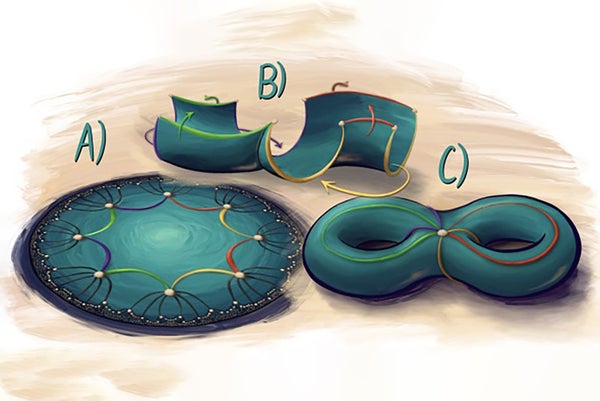
例如,这可能看起来像用八边形平铺弯曲表面,以便在非重叠的形状之间没有任何间隙。雷恩指出,在人类看来,这些八边形的边缘看起来是弯曲的,并且形状看起来大小不同。但是,“如果你有一种不同的眼睛,以双曲的方式看待世界——也许像昆虫的复眼——[八边形] 对你来说可能看起来都一样,”他说。
这项工作受到了其他研究人员的广泛关注。“我对这篇论文的作者发现的材料科学和代数几何之间的联系印象非常深刻,”多伦多大学的数学家迈克尔·格罗切尼格说,他没有参与这篇文章。
雷恩很高兴将他的发现应用于研究具有“颠覆性应用”潜力的不寻常材料,例如在量子计算中。“看到有人展示了这些方法在如此具体性质的重要应用,真是令人高兴,”格罗切尼格说。该论文“邀请我们纯粹的数学爱好者稍微离开我们的舒适区,去探索迄今为止未知的领域,”他补充道。
转化为音乐
创作一场数学音乐会本身就是对这项研究的一种颠覆性应用。“我不希望[音乐]是印象派的,”普雷斯拉夫说。“我希望它真正忠实于数学……我见过太多跨学科项目,它们给我的印象只是肤浅的。科学方面可能很严谨,而艺术方面则非常不严谨。”
雷恩同意这一目标。“我承诺不仅要创作一些松散地受到数学和科学启发的音乐,而且还要以音乐形式逐字逐句、逐个公式地复述数学,”他说。
但是,接受这一挑战也要求两位专家离开他们的舒适区,并相互学习对方专业领域的概念。普雷斯拉夫沉浸在线性代数和拓扑学的专题中,这有助于阐明研究论文的内部运作原理。雷恩则投入到“尽可能多地理解[普雷斯拉夫]提出的高级音乐理念”中。
在普雷斯拉夫甚至开始创作音乐之前,两人交流想法大约 18 个月。“令人惊讶的是,直到 9 月 20 日演出前一天,我才在现实生活中见到杰夫,”雷恩说。“这一切都是通过 Zoom 进行的,因为疫情和距离的原因。这是一种令人着迷的工作方式——我们甚至可以通过纯粹的虚拟方式完成这项工作。”
双重赋格曲和无限形状
很难准确指出雷恩和普雷斯拉夫是否实现了他们的宏伟目标:将雷恩论文中的主要思想直接转化为爵士音乐。与数学研究不同,没有“证明”表明他们实现了目标。不过,两人对他们的成果感到满意。“在演出前甚至六个星期,完成这件事都从来不是一件确定的事情,”雷恩说。
双曲乐队的演奏者沙阿·萨迪科夫是一位居住在巴尔的摩的中提琴家,他说音乐会的一个亮点是普雷斯拉夫使用了一种“非常难以实现”的双重赋格曲,来表示构建“无限形状”的过程,萨迪科夫说。从数学上讲,这意味着创建一个“没有开始,没有结束”的物体,萨迪科夫说。从音乐上讲,创作双重赋格曲包括使“一个想法成为音乐作品的基础,然后你采用完全相同的想法[并且]你将它稍后放在它的顶部”,等等,他说。“你创造了这些想法的层次。然后你可以使用与此相反的想法,要么采用相同的音乐想法[并且]将其向后或向上放置,”他指出。
对于雷恩来说,一个亮点是听到普雷斯拉夫对“所谓的粒子-波二象性或双曲能带理论中的位置-动量二象性”的音乐演绎。在这种情况下,动量可以比位置占据更多的维度。“我们想在音乐中捕捉到从比如说二维到四维的跳跃,在最简单的这些材料中,这些材料是基于八边形双曲晶格的,”雷恩说。
“听到[普雷斯拉夫]尝试在音乐中引入额外的声音,以捕捉额外的自由度,突然跳跃到额外的两个维度,对我来说是一次感人的经历,”雷恩说。“我喜欢看着观众在[他]解释之后试图听到那些额外的声音。”
音乐会还包括另一项艺术元素:基恩泽的手绘插图。基恩泽现在是加州大学伯克利分校的研究生,他为一个相关的研究项目创作了数学艺术作品,这是他和雷恩在他在马里兰大学帕克分校读本科时一起完成的。“这是一种尝试通过视觉镜头讲述故事的方式,”雷恩说。在音乐会中,这些插图帮助增强了对数学和科学的音乐和口头解释。
雷恩认为,通过音乐和艺术的视角重新诠释这项工作,是一种使其走向圆满的方式。他的论文中使用的许多数学和科学概念都借鉴了艺术世界的思想。例如,“双曲平铺非常让人联想到”荷兰图形艺术家 M. C. 埃舍尔的标志性木刻,他指出。雷恩计划继续探索融合数学和艺术视角的新方法,以便在为艺术“回馈”的同时,也为他的研究萌生新的见解。