
以下文章经许可转载自 The Conversation,这是一个报道最新研究的在线出版物。
假设你正在计划你的下一个派对,并且为客人名单绞尽脑汁。你应该向谁发送邀请函?朋友和陌生人的哪种组合才是合适的搭配?
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您正在帮助确保未来继续有关于塑造我们当今世界的发现和思想的具有影响力的故事。
事实证明,数学家们已经研究这个问题的一个版本将近一个世纪了。根据你想要什么,答案可能会很复杂。
我们的书《图论的迷人世界》探讨了这类谜题,并展示了如何通过图论来解决它们。像这样的问题可能看起来很小,但它漂亮地展示了图论如何被用于解决科学、通信和社会等不同领域的数学问题。
谜题的诞生
虽然众所周知哈佛是美国顶尖的学术大学之一,但您可能会惊讶地得知,哈佛曾经拥有全国最好的橄榄球队之一。但在 1931 年,在 全美四分卫巴里·伍德 的带领下,情况确实如此。
那个赛季哈佛对阵陆军。出乎意料的是,上半场结束后,陆军以 13-0 领先哈佛。显然感到沮丧,哈佛校长告诉陆军学员指挥官,虽然陆军在橄榄球方面可能比哈佛强,但哈佛在更学术的比赛中更胜一筹。
尽管哈佛队后来以 14-13 击败了陆军,但指挥官接受了在更学术的领域与哈佛竞争的挑战。双方同意在数学领域进行比赛。这导致陆军和哈佛选拔了数学队;对决于 1933 年在西点军校进行。令哈佛惊讶的是,陆军获胜了。
哈佛-陆军竞赛最终促成了 1938 年为本科生举办的年度数学竞赛,称为 普特南考试,以哈佛校长威廉·洛厄尔·普特南的亲属命名。这项考试旨在激发美国和加拿大数学领域的良性竞争。多年来,直到今天,这项考试都包含许多有趣且通常具有挑战性的问题——包括我们上面描述的问题。
红色和蓝色线条
1953 年的考试包含以下问题(略有改动):平面上有六个点。每两个点之间都用一条线连接,这条线要么是蓝色,要么是红色。证明在这六个点中,存在三个点,它们之间只绘制了相同颜色的线。
在数学中,如果存在一组点,并且某些点对之间绘制了线,则该结构称为图。对这些图的研究称为图论。然而,在图论中,点称为顶点,线称为边。
图可以用来表示各种各样的情况。例如,在普特南问题中,一个点可以代表一个人,红线可以表示这些人是朋友,蓝线可以表示他们是陌生人。
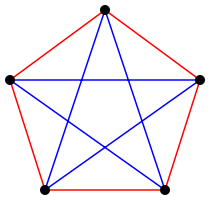
证明存在三个点,它们之间用相同颜色的线连接。致谢:richtom80 Wikimedia (CC BY-SA 3.0)
例如,我们称这些点为 A、B、C、D、E、F,并选择其中一个点,比如 A。从 A 到其他五个点绘制的五条线中,必须有三条线是相同的颜色。
假设从 A 到 B、C、D 的线都是红色的。如果 B、C、D 中任意两点之间的线是红色的,那么就存在三个点,它们之间只有红线。如果 B、C、D 中任意两点之间的线都不是红色的,那么它们都是蓝色的。
如果只有五个点呢?可能不存在三个点,它们之间所有的线都着相同的颜色。例如,线 A-B、B-C、C-D、D-E、E-A 可能是红色的,而其他线是蓝色的。
从我们所看到的,可以得出结论,邀请参加派对(每两个人要么是朋友,要么是陌生人)的最小人数是六个,这样才能保证有三个共同的朋友或三个共同的陌生人。
如果我们想要四个相互认识的朋友或四个相互不认识的陌生人呢?为了确保这一点,我们必须邀请参加派对的最小人数是多少?这个问题已经有了答案。是 18。
如果我们想要五个相互认识的朋友或五个相互不认识的陌生人呢?在这种情况下,为了保证这一点,需要邀请参加派对的最小人数是——未知的。没有人知道。虽然这个问题很容易描述,听起来也相当简单,但它却出了名的难。
拉姆齐数
我们一直在讨论的是图论中的一种数字,称为拉姆齐数。这些数字以英国哲学家、经济学家和数学家 弗兰克·普伦普顿·拉姆齐 的名字命名。
拉姆齐在 26 岁时去世,但在他很小的时候就获得了一个非常奇特的数学定理,这引发了我们这里的问题。假设我们有另一个充满点的平面,这些点通过红色和蓝色线条连接。我们选取两个正整数,分别命名为 r 和 s。我们希望恰好有 r 个点,它们之间所有的线都是红色的,或者有 s 个点,它们之间所有的线都是蓝色的。我们可以用最少多少个点来做到这一点?这叫做拉姆齐数。
例如,假设我们希望我们的平面至少有三个点通过全红线连接,并且有三个点通过全蓝线连接。拉姆齐数——我们需要使这种情况发生的最小点数——是六。
当数学家看待一个问题时,他们经常问自己:这是否暗示了另一个问题?这就是拉姆齐数——以及派对问题——的情况。
例如,这里有一个问题:五个女孩正在计划一个派对。她们决定邀请一些男孩参加派对,无论她们是否认识这些男孩。她们需要邀请多少个男孩才能确保在男孩中始终有三个男孩,并且五个女孩中的三个女孩要么与这三个男孩都是朋友,要么与这三个男孩都不认识?可能不容易猜到答案。答案是 41!
已知的拉姆齐数非常少。然而,这并没有阻止数学家们尝试解决此类问题。通常,未能解决一个问题可能会导致一个更有趣的问题。这就是数学家的生活。
本文最初发表于 The Conversation。阅读 原文。
