我高中时并没有觉得数学特别令人兴奋。 老实说,我上大学后才开始学习数学,因为最初它对我来说似乎很容易。 但在我本科生涯的第一堂数学课上,我意识到我对数学的一切认知都是错误的。 数学一点也不容易。 我很快发现,数学可以非常令人兴奋,尤其是当你超越纯算术领域时。
在物理学中,真正令人惊讶的内容——那些与你对宇宙的直觉相悖的概念——大约在高中时出现,那时学生们可以瞥见奇异的量子世界,并接触到爱因斯坦的广义和狭义相对论。 学校数学无法跟上这些奇迹。 你学习基本的算术运算、积分和求导、概率和向量的基本处理。 如果你幸运的话,有抱负的老师可能会向你展示一个简单的证明。 就这样。 因此,难怪许多学生未能对这门学科培养真正的热情。
然而,数学提供了各种各样的惊喜,例如巴拿赫-塔斯基悖论,它指出你可以几乎神奇地将一个球体翻倍,或者存在无限多个不同的无穷大。 真正让我震惊的是发现数学与最奇异的物理现象是如此深刻地交织在一起。 并非一定是量子物理本身产生了令人难以置信的效果; 不,系统始终遵循严格的数学规则。 正如化学家彼得·阿特金斯在他 2003 年出版的《伽利略的手指》一书中所说,“确定数学在哪里结束,科学在哪里开始,就像描绘早晨薄雾的边缘一样困难且毫无意义。”
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。 通过购买订阅,您将有助于确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
物理学家迈克尔·贝里的一项发现比任何例子都更好地说明了数学和物理学的融合。 1984 年,贝里揭示了量子力学深刻且在很大程度上出乎意料的几何方面。 贝里意识到,这种几何赋予了量子粒子一种记忆。
实际上不应该发生任何事情
当时,贝里正在研究一个非常简单的系统:处于变化环境中的粒子(例如中子)的量子态。 中子具有一种称为自旋的量子特性,它就像粒子随身携带的微小磁铁。 这种自旋可以向上或向下定向——因此物理学家说中子具有“自旋向上”或“自旋向下”。 中子的自旋受外部磁场的影响。
贝里使用数学方法来研究如果磁场方向缓慢变化,中子会发生什么。 根据 20 世纪初提出的所谓绝热定理,粒子的量子性质不应因此而改变:其能量、动量、质量和自旋保持不变。
如果你缓慢地转动磁场的方向,然后再将其移回原始方向,原则上,这种动作实际上不应该改变任何东西。 “至少,多年来,这在物理学家中是一种普遍的观点,”贝里在 1988 年 12 月的《大众科学》杂志上的一篇文章中写道。 但“波函数相位的变化被忽略了。”
量子力学最奇怪的现象之一是波粒二象性:量子物体可以被想象成点状形状,但它们也表现出像水一样的波动行为。 相位描述了波相对于某个角度的位移——例如,余弦函数只不过是相位移动的正弦函数。
正如贝里在他的计算中认识到的那样,磁场的缓慢变化会导致中子的波函数旋转一定的相位。 这意味着粒子的波函数显示了过去发生的事情(在本例中为磁场的变化)。 此外,贝里认识到,这种相位不仅发生在粒子在磁场中的特殊情况下。 量子系统缓慢改变然后返回到其原始条件的各种情况都会在波函数中留下痕迹。
贝里的开创性工作发表后不久进行的实验证实了这些想法。 如果你熟悉量子力学,那么你可能知道波函数不是一个可以直接观察到的量。 然而,有一种方法可以通过使用第二个粒子作为参考来测量相移。 在这些实验中,物理学家允许两个粒子(例如中子)碰撞,其中一个粒子之前处于可变磁场中。 当中子相遇时,它们的波函数相互作用。
这些函数的行为类似于水波:如果波谷和波峰对齐,它们会相互加强; 另一方面,如果它们彼此错开,它们会减弱或完全消失。 这些现象分别称为相长干涉或相消干涉。
实验表明贝里是正确的:中子是异相的,发生相消干涉。 这一观察结果表明,其中一个粒子曾经短暂地处于变化的磁场中。 即使其任何可测量的性质都没有因此而直接改变,但其改变的波函数暴露了这一点。
弯曲的宇宙
但是贝里是如何知道粒子会经历相移的呢? 事实上,只要存在曲率,就会出现这种相位。 这就是为什么相位在爱因斯坦的广义相对论中起着重要作用——他用该理论来描述引力。
一些专家认为,广义相对论更多的是几何学而不是物理学。 根据该理论,物质弯曲时空,而这种变形导致质量相互吸引——我们将其感知为引力现象。 我喜欢把它想象成一张橡皮片,上面放置着重物,使橡皮片变形,从而影响物体。 然而,这种可视化存在一些缺陷:时空在这个概念中是二维的,我从我的三维世界俯视它。 另一方面,广义相对论描述了四维时空的曲率,而无需从五维视角来看待它。
这就提出了一个问题,如果你不能从外部观察物体,你如何推断出物体的曲率? 贝里观察到的相位在这里有所帮助。
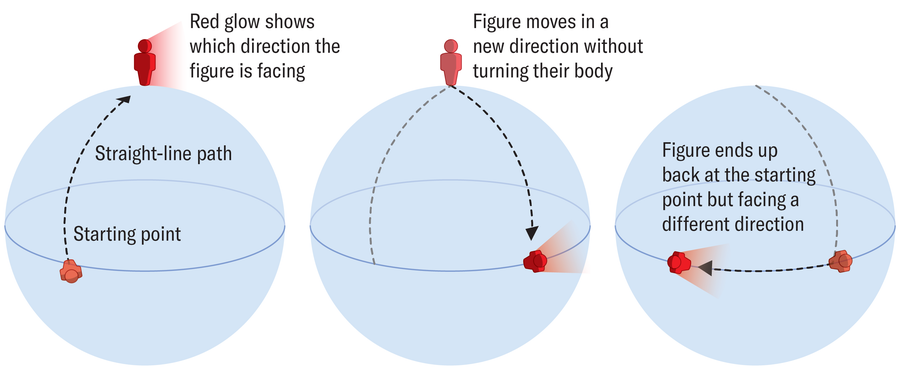
假设我想用一种复杂的方式证明地球是球体。 为了做到这一点,我可以从我在德国某地的位置笔直向北走,越过山脉、山谷、河流、湖泊和海洋。 在这个思想实验中,没有什么可以阻止我沿着直线路径前进。 当我到达北极时,我像螃蟹一样横着走,向右移动,而无需转身。 我一直走到与我开始时相同的纬度。 然后我沿着纬度向左走——同样无需转身——直到我回到起点。 虽然我降落在原来的位置,但我不再像开始时那样面向北方,而是面向东方。 因此,这次往返旅行并没有改变我这个人(除了可能身体上的劳累),但我已经转动了一定的角度。
阿曼达·蒙塔内斯
如果我沿着平坦的平面走相同的路径,我会在没有任何旋转的情况下返回起点。 但在这个设置在我们弯曲的星球上的思想实验中,发生在我身上的事情与贝里理论中的波函数相同:它接收到一个相位,一个使其移动的角度。
我在旅途中获得的这个角度完全取决于地球的几何形状。 其值与我的路径所包围的面积成正比。 因为没有其他因素影响相位——既不是我的速度,也不是我是否休息——所以它被称为“几何相位”。
对于数学家来说,这在贝里发表他的著作时并不是什么新鲜事。 他们几十年前就知道了这个概念。 但没有人将几何相位应用于量子力学过程。 波函数中的相位揭示了所谓的参数空间的几何形状。 这是一个抽象的、高维的空间,它结合了所有可能影响波函数的参数(例如磁场、能量、位置和速度)。 磁场方向(或其他参数)的短期变化描述了这个空间中的一条闭合曲线——就像我在地球上的圆形路径一样。 因为这个参数空间通常是弯曲的,这会在波函数中留下痕迹。
“因此,几何相位可以被视为系统对‘系统在参数空间中采取了什么路径?’这个问题的最佳答案,”贝里在他的 1988 年《大众科学》文章中写道。“从这个意义上说,它是一种量子‘记忆’。”
因此,贝里揭示了量子系统和几何学之间深刻的联系,事实证明这是非常有价值的。 以他的名字命名的贝里相位可以用来解释量子霍尔效应等现象,这种效应发生在某些固体中,并在贝里发现之前提出了许多问题。
所有这一切都非常令人兴奋。 然而,对我来说,最令人印象深刻的是,贝里通过借鉴现有的数学概念,开创了几何量子物理学这一新的研究领域。 他不必在物理学或数学中添加任何新东西——相反,数学使揭示物理学中完全出乎意料的东西成为可能。
本文最初发表于《Spektrum der Wissenschaft》,经许可转载。
