信任但要核实。这种表达捕捉了依赖他人和仍然希望保持对局势一定程度控制之间的紧张关系。数学家阿迪·沙米尔在开发现在被称为“沙米尔秘密共享”的算法时,一定考虑过这个挑战,该算法以他的名字命名。
为了理解它,以下谜题可以提供帮助:假设一位老妇人想将她的保险箱(用密码锁保护)的内容遗赠给她的五个儿子,但她对他们每个人都持怀疑态度。她担心如果她只向其中一个儿子透露密码,他就会带着里面的东西逃之夭夭。因此,她想给每个儿子一个线索,只有五个儿子一起工作才能打开保险箱。这位妇人应该怎么做?
这项任务可能看起来很简单。例如,如果密码锁需要一个五位数的密码,她可以给每个儿子一个数字,以便他们可以一起打开它。但在这种情况下,如果三个儿子联手,他们很可能会绕过其他两个兄弟。三个盟友只差两个数字才能得到完整的密码,因此他们可以快速尝试可能的数字组合以获得梦寐以求的内容。
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您正在帮助确保有关塑造我们今天世界的发现和想法的具有影响力的故事的未来。
因此,这位妇人正在寻找一种分发信息的方式,这种信息只有在所有五个儿子一起工作时才能使用。如果五个儿子中的两个、三个或四个聚在一起,组合后的信息内容必须是无用的。而这个要求使任务变得更加复杂。
但在 1979 年,这个挑战并没有让沙米尔气馁。两年前,他与罗恩·李维斯特和伦纳德·阿德曼一起开发了所谓的“RSA 算法”。这是第一个被广泛采用的非对称加密算法,至今仍在使用。
沙米尔秘密共享的实际应用
为了理解沙米尔秘密共享方法,查看一个具体的数字示例会有所帮助。假设这位妇人的秘密代码是 43953,并且为了简单起见,我们假设她只有两个儿子。(我们稍后将逐步解决有五个儿子的情景。)
如果这位妇人委托一个儿子“439”,另一个儿子“953”,她就给了他们两人相同数量的信息。现在,如上所述,儿子们可以各自尝试猜测缺少的两位数字。他们每个人最多只需要尝试 100 个组合即可打开保险箱。
因此,沙米尔需要不同的解决方案。最好是每个儿子收到的信息乍一看与解决方案无关。但是,如果将两条信息放在一起,您应该能够推断出数字组合 43953。并且有一种优雅而简单的方法可以借助线性方程来做到这一点。
每条直线都由两个点唯一确定。沙米尔意识到秘密数字可以编码在一条直线上:例如,作为它与 y 轴相交的高度。如果您给两个儿子每个人在直线上一个点的坐标,他们只能一起确定数字 43953。一个儿子单独一个点什么也做不了:有无数条直线穿过一个点。
例如,这位妇人可以选择直线方程 y = 5x + 43953,并给大儿子一个点 P1 (33503, 211468) 的坐标,给另一个儿子第二个点 P2 (85395, 470928) 的坐标。即使这两个儿子的数学不好,他们也可以简单地在平面上标记这两个点,用尺子连接它们,然后读出直线与 y 轴的交点,即可得到保险箱的解决方案。
因此,两个儿子的问题就解决了。如果这位妇人有三个儿子,她可以以类似的方式进行。然而,在这种情况下,她不会选择直线,而是选择抛物线来隐藏代码。
例如,这位妇人可以选择二次函数 y = 5x2 + 10x + 43953,并给她的每个儿子一个抛物线上的点。同样,与 y 轴的交点对应于所需的解决方案:43953。两个儿子不能合谋反对第三个儿子,因为无数条抛物线可以穿过两个点;两个儿子需要他们兄弟的帮助才能找到与 y 轴的交点,从而找到保险箱的密码。
该原理可以推广到任意数量的参与者:有四个儿子的妇人可以解方程 y = ax3 + bx2 + cx + 43953。(因为 3 是此方程中的最高指数,所以它被称为三次多项式方程。)有五个儿子的妇人使用四次多项式方程(例如 y = ax4 + bx3 + cx2 + dx + 43953),依此类推。该原理基于所谓的“多项式插值”:一般来说,需要 n + 1 个点才能唯一确定 n 次多项式。
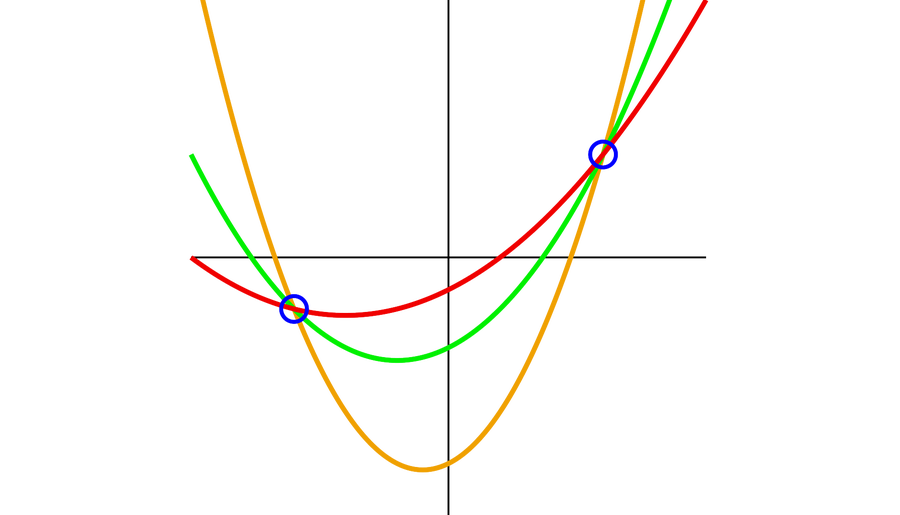
有无数条抛物线穿过两个点。 来源:Vlsergey/Wikimedia (CC BY-SA 3.0)
这位妇人还可以让她的儿子们成对访问保险箱。在这种情况下,她依靠儿子们互相控制,因此需要五个人中的两个人同时在场才能打开保险箱。为此,这位妇人可以再次选择一条直线作为基础,并在其上标记五个随机选择的点。通过给每个儿子一个点,她确保他们中的两个人可以确定密码——无论哪两个儿子相遇。
但这里有一个问题。让我们回到有五个儿子的情景。如果他们中的四个合谋反对一个兄弟,他们可以使用这四个点尽可能地解出四次方程。当然,他们无法直接从中读取密码。最后,他们留下了一个带有两个未知数的方程:参数 a 和密码 c(在我们的示例中是 43953,但儿子们不知道)。
然而,这四个儿子知道 c 必须是整数。例如,如果这位妇人总是给他们曲线上点的整数坐标,那么他们可以假设 a 可能也具有整数值。这大大限制了可能性的范围。兄弟们可以使用计算机程序尝试不同的解决方案——然后可能会确定正确的密码。
进入不同的数字范围
为了避免这种情况,沙米尔还有另一个诀窍:他没有使用通常的实数进行计算,而是将自己限制在一个更小的数字空间:有限域。在这个数字系统中,四种基本算术运算(加法、乘法、减法和除法)可以像往常一样应用。然而,这个数字空间不是包含无限数量的数字,而是只包含有限数量的数字。

如果您想确定 n 次多项式,您至少需要 n+1 个点。 来源:MartinThoma/Wikimedia (CC BY-SA 3.0)
虽然这听起来可能很陌生,但我们每天都在使用有限域——例如,每当我们看时钟时。如果您只看小时,数字范围包括 12 或 24 个数字。但我们仍然在这个有限的空间中计算:如果现在是晚上 11 点,有人说面包店七小时后开门,那么很明显他们指的是六点钟。
在沙米尔秘密共享中,也选择了一个受限的数字范围,但上限通常是一个大的质数。如果以这种方式选择数字空间,则多项式的图形不再对应于连续曲线,而是对应于平面中随机分布的点。
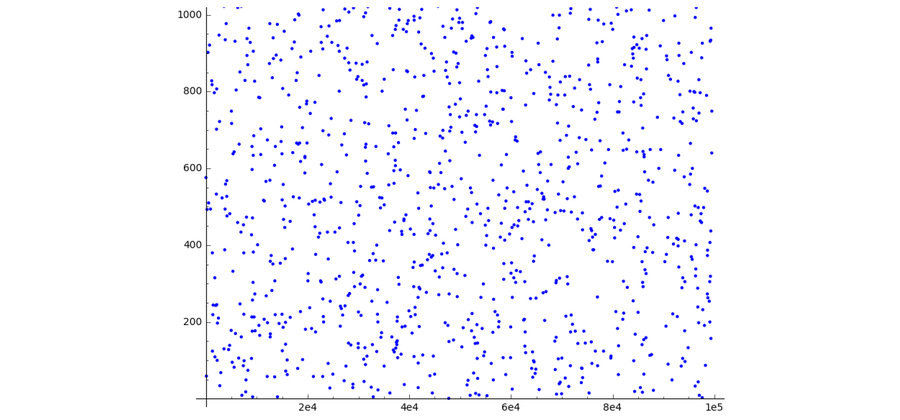
当您在有限域中定义多项式方程时,平滑曲线会变成一组点。 来源:Wolfmankurd/Wikimedia (CC BY-SA 4.0)
通过将这位妇人的计算限制在这样的数字范围内,兄弟们实际上不可能合谋反对彼此。为了找出正确的数字代码,他们必须一起工作。
本文最初发表于Spektrum der Wissenschaft,并经许可转载。
