古代学者希帕索斯因发现无理数而被处死——或者至少传说如此。公元前五世纪究竟发生了什么,目前尚不清楚。
希帕索斯是毕达哥拉斯学派的成员,这是一个涉及数学和数字神秘主义的教派,以及其他事物。毕达哥拉斯学派教义的核心要素与和谐的数字关系有关,其中包括整数的分数。
他们认为,整个世界都可以用有理数来描述,包括自然数和分数。然而,故事是这样的,当希帕索斯检查毕达哥拉斯学派的象征——五角星的长度比率时,他意识到该形状的某些边的长度无法表示为分数。因此,他提供了无理数存在的第一个证明。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您正在帮助确保有关塑造我们今天世界的发现和想法的具有影响力的故事的未来。
从这里开始,关于希帕索斯的说法开始分歧。有些人说毕达哥拉斯学派对这种断言感到不满,因为这样的数字与他们的世界观背道而驰。在其他故事中,希帕索斯公开了他的成果,因此违反了该教派的保密性。无论如何,他在发现后溺水身亡。一些报道声称毕达哥拉斯学派将他从船上扔下去。其他人则断言他的死是一场意外,毕达哥拉斯学派认为这是神圣的惩罚。
目前对现有历史证据的解读表明,这些故事纯属传说。希帕索斯的发现——假设他真的做出了这个发现——很可能被誉为一项数学成就,令毕达哥拉斯学派感到自豪。事实上,围绕毕达哥拉斯学派的许多可疑故事都是因为他们因其哲学和政治思想而受到迫害。
可用的事实有限。这个社团很可能由萨摩斯的毕达哥拉斯在现在的意大利南部创立——这位希腊学者以著名的勾股定理命名(尽管他是否证明了这个定理也不清楚)。除了对数学的兴趣外,毕达哥拉斯学派还有许多观点使他们与古希腊其他人区分开来。他们拒绝财富,过着素食主义的苦行生活,并相信轮回。最终,该团体遭受了几次袭击,在毕达哥拉斯去世后,该社团完全消失了。
关于希帕索斯的故事,历史学家一致认为最有可能真实的要素是,毕达哥拉斯学派在某个时候证明了某些量是不可公度的,由此推导出无理数的存在。
分数之外的数字
我们现在在学校里了解到,有些值——所谓的无理数——无法表示为两个整数的比率。但这种认识远非显而易见。毕竟,无理数值至少可以用分数来近似——尽管有时这很困难。
希帕索斯——或另一位毕达哥拉斯学派成员——提出的著名的无理数证明最容易用等腰直角三角形来说明:考虑一个两条边长均为a的三角形,这两条边形成一个直角,与长度为c的斜边相对。
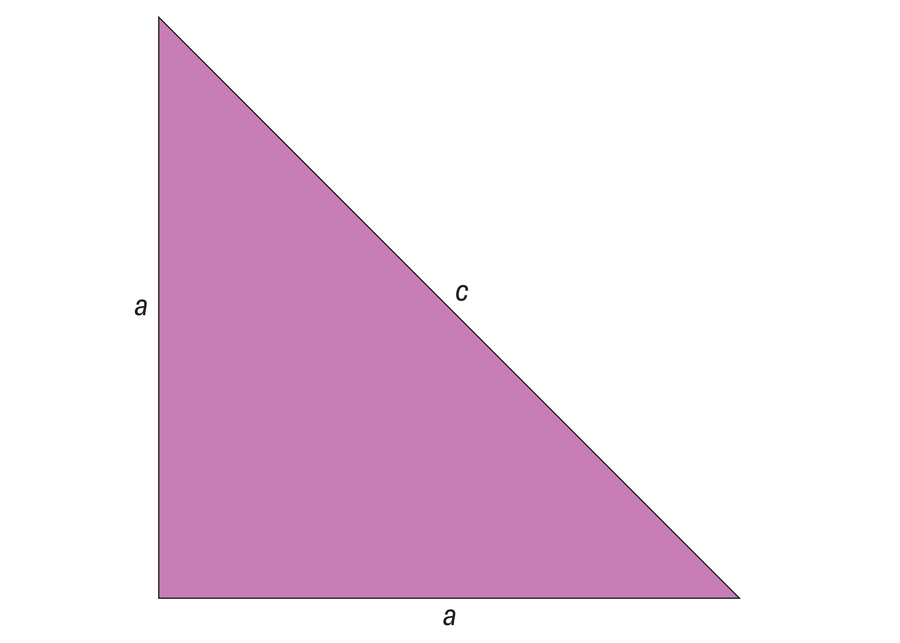
无理数的存在最好用等腰直角三角形来解释——也就是说,一个两条边长度相等并形成直角的三角形。
Manon Bischoff/Spektrum der Wissenschaft
这样的三角形具有固定的纵横比a⁄c。如果a和c都是有理数,则可以选择三角形的边长,使a和c各自对应于可能的最小自然数(即它们没有公约数)。例如,如果纵横比为2/3,您将选择a = 2 和 c = 3。假设三角形的长度对应于有理数,则a和c是整数并且没有公约数——或者至少每个人都这么认为。
反证法
希帕索斯使用这种思路来创建一个矛盾,这反过来证明了最初的假设一定是错误的。首先,他使用勾股定理(古老的a2 + b2 = c2)将斜边c的长度表示为两条等边a的函数。或者,用数学方式表达:2a2 = c2。由于a和c是整数,因此从前面的方程可以得出c2必须是偶数。因此,c也可以被2整除:c = 2n,其中n是自然数。
将c = 2n代入原始方程得到:2a2 = (2n)2 = 4n2。2可以在两边约简,得到以下结果:a2 = 2n2。由于a也是一个整数,因此得出a是平方数,因此也是一个偶数。然而,这个结论与最初的假设相矛盾,因为如果a和c都是偶数,则它们都不能是除数。
这个矛盾使希帕索斯得出结论,等腰直角三角形的纵横比a⁄c不能对应于有理数。换句话说,存在一些数字无法表示为两个整数值的比率。例如,如果形成直角的边a = 1,则斜边c = √2。正如我们今天所知,√2是一个无理数,其小数位无限期地延续下去,永不重复。
从我们目前的角度来看,无理值的存在似乎并不太令人惊讶,因为我们在很小的时候就接触到了这个事实。但我们只能想象,大约2500年前的这种认识可能会引发什么。它可能会颠覆数学世界观。因此,关于它的发现有如此多的神话和传说也就不足为奇了。
本文最初发表于《Spektrum der Wissenschaft》,经许可转载。
