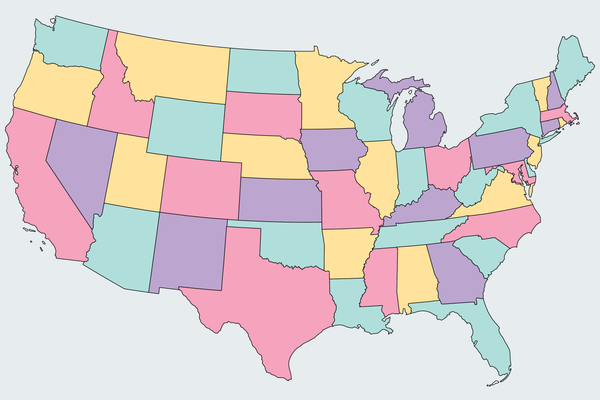
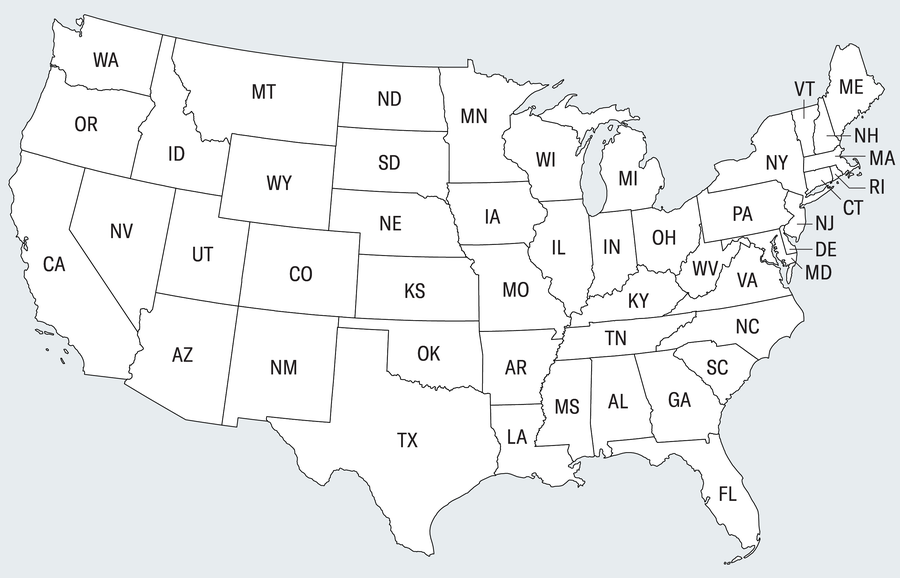
1852 年,数学家弗朗西斯·格思里提出了一个看似简单的问题,这个问题引发了无休止的争论,导致大量已发表的论文被推翻,并最终以一种突破数学原则的方式得到解决。这个引起如此多麻烦的难题是:为地图着色所需的最小颜色数是多少,才能使相邻的州或其他指定区域不具有相同的颜色?以下是它的工作原理。看看下面美国本土的黑白地图。它看起来有点简陋。为了使地图更生动并清晰地突出其边界,制图师倾向于为区域着色。
金俊
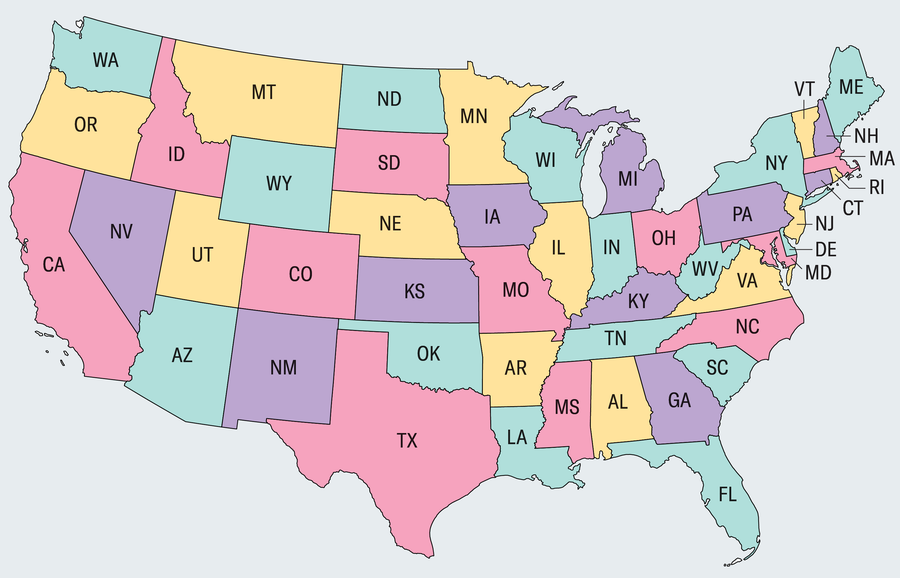
当然,我们不希望相邻的州具有相同的颜色,因为那样会使边界更加混乱。在这种约束下,我们使用了四种颜色来填充黑白地图。我们只用三种颜色可以做到吗?其他地图可能需要五种或六种颜色吗?
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
金俊
这个问题中的地图不必对应真实的地理位置——任何将平面表面划分为不同区域的方式都符合条件。问题是,给定任何这样的地图,需要多少种颜色来填充每个区域,才能使没有两个相邻区域具有相同的阴影。一些基本规则:每个不同的区域必须是连通的(从技术上讲,密歇根州在美国地图中违反了这一规则,因为密歇根湖将该州分割成两个不连通的部分)。要使两个区域被视为相邻,它们必须共享一定长度的连续边界;仅在一个点(或离散的点集)接触不符合条件。例如,犹他州和新墨西哥州仅在一个角上接触,因此在我们的目的中不被视为邻居。
在规则确立后,这里有一些答案令人惊讶的问题。假设我打印出一张包含数千个区域的复杂地图的大海报。您需要多长时间才能确定该地图是否可以用两种颜色着色?三种颜色?四种颜色?您不一定需要找到 着色方案;只需确定每种颜色数量是否存在即可。奇怪的是,尽管对于所有数字来说,任务看起来几乎相同,但完成每种颜色数量的任务所需的时间却截然不同。使用最著名的方法
确定两种颜色是否足够大约需要一个小时。要做到这一点,选择任何区域并为其着色,例如红色。这会将该区域的所有邻居强制变为您的第二种颜色,例如蓝色。反过来,它们的所有邻居都变成红色,依此类推,在地图上蔓延。最终,您要么遇到邻近区域共享颜色的冲突,在这种情况下,不存在“双色着色”,要么颜色在整个地图中无冲突地传播,在这种情况下,您就找到了有效的着色方案。根据粗略计算,对于包含 3,000 个区域的地图,以每着色方案一秒的速度计算,需要花费 50 分钟的时间。
假设地图无法仅用两种颜色填充。确定三种颜色是否足够将需要更长的时间。下午会悄然流逝。当您疯狂地涂写无尽的配置,寻找可行的配置时,几周的时间也会从日历上剥落。为了继续进行下去,您必须将正在进行的任务传递给您的孩子,然后再传递给他们的孩子。几代人的生命都致力于寻找这张地图的三色着色方案,也无法撼动这项工作量,因为太阳在数十亿年后不可避免地吞噬地球,并结束这种愚蠢的努力,使我们几乎无法接近答案。
确定任意地图是否具有三色着色方案是困难的。这里的“困难”是一个技术术语,表示它属于一类以其耗时难度而闻名的计算问题,称为 NP 完全问题。对于此类问题,我们不知道任何比或多或少地蛮力搜索每个可能的解决方案更快的方法。随着问题规模的增加,搜索空间呈指数级增长。对于只有少量区域的小地图,我们可以负担得起穷尽搜索每种可能的三色着色方案,直到找到可行的方案(或得出结论,认为不存在可行的方案)。但是,为包含数千个区域的地图分配三种颜色的方式数量是如此之大,以至于穷举搜索变得毫无希望。
那么四种颜色呢?嗯,这大约需要一秒钟,或者您需要说“是”的时间,因为每张地图都可以用四种颜色着色。这个结果就是臭名昭著且长期存在争议的四色定理。
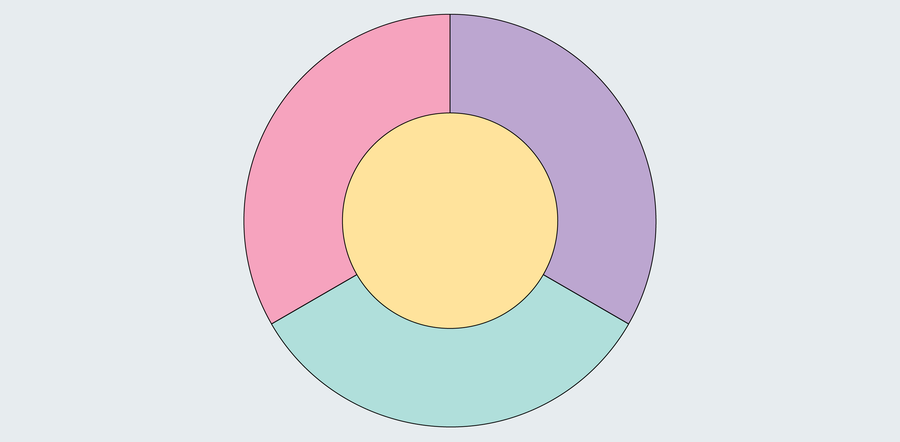
当格思里在 1852 年首次推测四色定理时,他注意到他只需要四种颜色就可以正确地填充英格兰的县。他怀疑这条规则可以推广到任何地图,但是尽管任何幼儿园的孩子都能理解这个问题,但他和他的同事都无法证明它。很明显,三种颜色并不总是奏效,如下面的圆形图所示,其中每个区域都与所有其他区域相邻。
金俊
但是没有人能找到需要五种颜色的地图。由于这个问题受阻,数学家奥古斯都·德·摩根对此变得痴迷,并得出结论,必须在数学基础上添加一个新公理——在数学中,公理是指未经证明而被假定为真的陈述,更复杂的陈述可以从中推导出来——以解决格思里的猜想。
这种狂热的挫败感表面上在 1879 年结束了,当时出现了一个证明,证明四种颜色总是足够的。一年后,第二个独立的证明强调了这一点。随着问题得到解决,荣誉也随之而来,被吸引的数学家回到了他们通常的研究工作中——除了一些人。在第一个证明发表 11 年后,两个证明都被推翻,而难以捉摸的四色定理又恢复为四色猜想。英格兰达勒姆大学的珀西·约翰·希伍德揭露了原始证明中的漏洞,但他取得了一些进展,证明五种颜色总是足以填充任何地图。
这使数学界处于相当尴尬的境地。一个看似如此简单的问题只有两个答案——四个或五个——但哪个是正确的?这种情况将持续近一个世纪。
尽管没有人能找到需要五种颜色的地图,但也没有人能排除存在这种地图的可能性。由于地图的数量是无限的,因此永远无法单独检查每张地图。解决问题的一个关键步骤是将问题简化为可以单独检查的有限的案例集。从无限到有限的飞跃似乎很大,但是要检查的案例的庞大数量仍然远远超过了任何人可以手动处理的数量。
因此,当时的伊利诺伊大学的数学家肯尼斯·阿佩尔和沃尔夫冈·哈肯转向了一个大胆的想法:编程计算机来处理它们。1976 年,经过多年的微调和超过 1,000 小时的计算机运行时间,他们的算法完成了对每个案例的穷举检查,并且四色定理得以确立。这是第一个在证明中使用计算机的重大定理。
数学界燃起了庆祝和沮丧并存的火焰。阿佩尔和哈肯在安大略省滑铁卢大学的同事威廉·塔特欣喜若狂,他们“击败了海怪。”其他人则鄙视计算机侵占人类智慧的想法。这件事也给数学界带来了一个哲学问题。人类无法验证的证明算作证明吗?许多人预计这项工作最终会被像之前的两个所谓证明一样撤回。《纽约时报》甚至拒绝在最初报道这一消息,因为四色定理的证明“反正都是假的。”
在随后的几十年中,多次尝试驳斥计算机辅助证明都失败了。数学家们此后大大简化了证明并验证了计算机代码,但时至今日,仍未发现任何无需计算机辅助即可推导出的定理证明。尽管四色定理已被广泛接受为事实,但对其仍存在渴望。系统分析大量配置的计算机程序并没有确切解释为什么每张地图都可以用四种颜色填充。即使数学家现在欢迎计算机作为发现的伙伴,他们仍在寻找对这个色彩缤纷的谜题更具启发性的证明。