“在过去,我们只能收到橙子作为礼物——而且我们为此感到高兴!” 这句话你有时会听到年长的人批评当今孩子们收到的礼物过于奢华。 但他们很少提到礼品包装。 假设你想送五个橙子作为礼物: 你会如何安排这些水果,使它们占用尽可能少的空间和包装纸?
事实证明,这个看似无害的问题背后隐藏着大量的数学知识。 毕竟,花了 400 多年才证明水果商们自古以来就知道的事情: 无限球体在三维空间中的最佳堆叠是通过将它们排列成金字塔形状来实现的。 针对这个谜题的已验证解决方案,被称为开普勒猜想,直到 2017 年才发表。 然而,当只考虑有限数量的物体时,情况就大不相同了。
令人惊讶的是,数学家们直到 19 世纪后期才开始研究后一种问题。 挪威几何学家阿克塞尔·图厄是 1892 年第一个研究有限数量的二维圆的最佳排列的人。 该领域的重要进展直到接下来的几十年才出现,当时匈牙利数学家拉斯洛·费耶斯·托特探讨了这个主题。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。 通过购买订阅,您正在帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。
平面上圆的最佳排列
为了更好地了解这个问题,首先考虑简化的二维情况会有所帮助。 例如,我们可以尝试以最节省空间的方式排列几个相同大小的硬币。 为此,我们用一段绳子勾勒出它们的轮廓,我们将绳子拉紧在一起,并计算绳子围成的面积。 对于 n = 2 个硬币,很快就能找到最佳排列方式: 我们将它们放下,使它们彼此接触。 然后,包围半径为 r 的两个硬币的最短绳子的长度为 (4 + 2π)r。
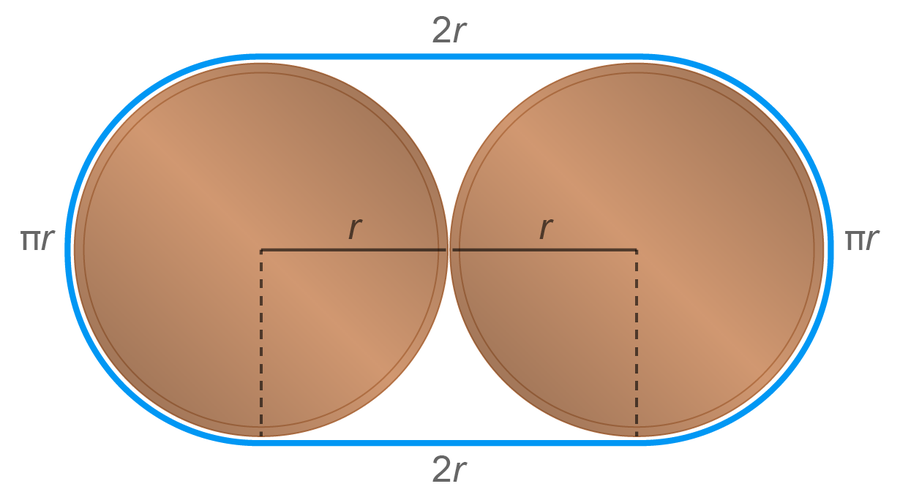
两个最佳包装的硬币配对。 来源: Spektrum der Wissenschaft/马农·比肖夫,由 大众科学 设计风格
这个长度最好按部分计算: 加上绳子的直线部分(4 x r),再加上总共围成一个圆的圆形区域(2πr)。 绳子围成的总面积为 (4 + π)r2。 在这种情况下,显然没有更节省空间的方式来排列硬币。
另一方面,如果手头有三个硬币,突然出现了两种不同的看起来节省空间的排列方式: 一种是将它们并排排列,另一种是将它们沿着等边三角形的角放置。 在第一种情况下,绳子会呈现香肠形状,这就是为什么在数学中它被称为“香肠”包装。 第二种情况被专家称为“披萨”包装。 但是哪种排列方式更节省空间: 香肠包装还是披萨包装?
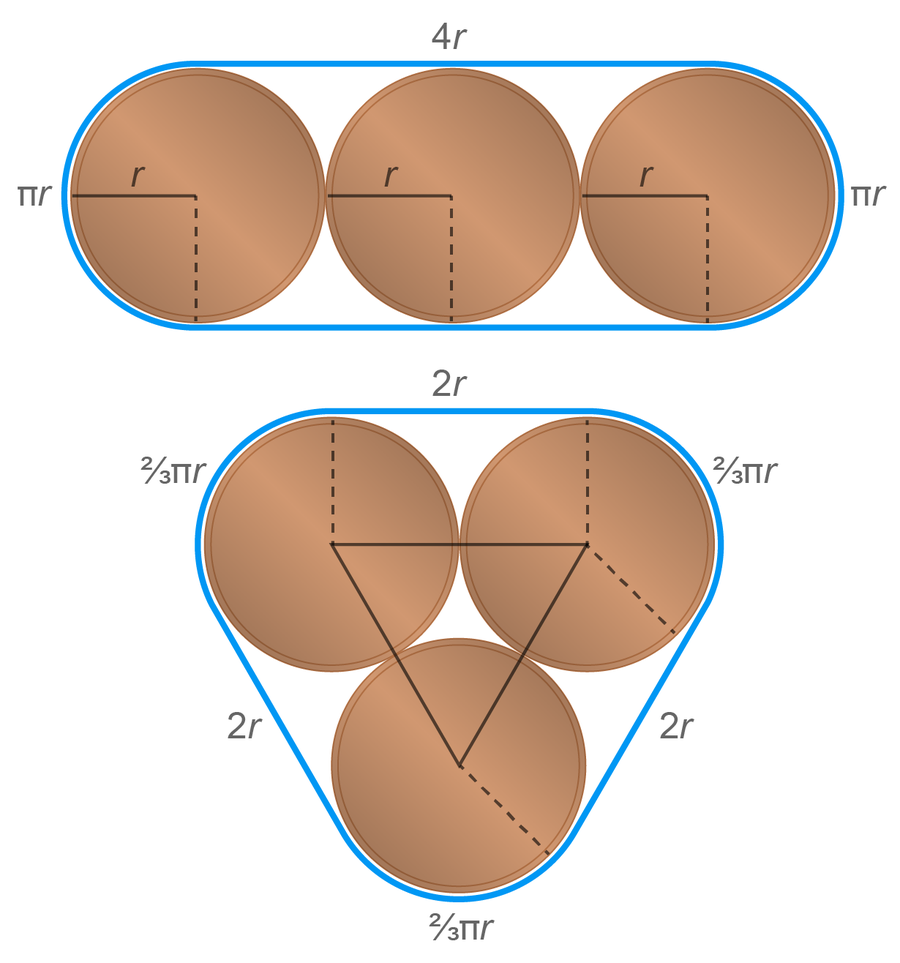
三种硬币的两种排列方式。 来源: Spektrum der Wissenschaft/马农·比肖夫,由 大众科学 设计风格
事实证明,披萨包装更好。 这种绳子的长度为 (6 + 2π)r,,覆盖的面积相应为 (6 + √ 3 + π)r2,而香肠包装的绳子长 (8 + 2π)r,围成的面积为 (8 + π)r2。 如果仔细观察,也可以直接从图片中看出这种差异。 香肠排列中硬币之间的空间比披萨包装中的空间更大。
在二维中,披萨总是胜出
事实上,可以给出绳子所需长度和限制面积的一般公式。 如果将 n 个硬币排列成香肠形状,则需要长度为 4(n – 1 + 2π)r 的绳子,它围成的面积为 4(n – 1)r2 + πr2 。 另一方面,如果硬币沿着三角形网格排列,其形状尽可能地类似于正六边形,则只需要长度为 2(n + π)r 的绳子,围成的面积为 (2n + √ 3(n – 2) + π)r2。
因此,我们已经证明,对于任何数量的 n 个圆,披萨包装都比香肠形状更节省空间。 但它真的总是最优的吗? 确定这一点是一项更加困难的任务。 毕竟,可能存在完全混乱的圆形排列,占用更少的面积。 排除这种情况被证明极其困难。 这就是匈牙利数学家拉斯洛·费耶斯·托特发挥作用的地方。 1975 年,他推测,n 个圆的最佳包装是在三角形晶格中的排列,该排列形成尽可能规则的六边形形状。
2011 年,数学家多米尼克·肯恩能够证明,这个想法适用于几乎所有 n 值。 事实上,无限平面上覆盖无限数量的硬币的极限情况也得到了证明。 1773 年,物理学家和数学家约瑟夫·路易斯·拉格朗日发现,沿着三角形晶格的排列是最优的——只要你只考虑有序包装。 直到 1940 年,费耶斯·托特最终证明,这个解决方案也比任何混乱的圆形排列更节省空间。
当香肠领先时
但是球体呢? 三维情况比二维世界中最佳圆形包装提出更多问题,这可能不足为奇。 我们至少有一个线索可以开始: 开普勒猜想指出,如果你像炮弹一样堆叠无限多个相同的球体,它们可以最好地填充三维空间。 在第一层,你沿着三角形网格排列它们,就像二维情况下的硬币一样,在第二层,你在每个间隙中放置一个球体。 然后第三层再次与第一层相同,依此类推。 (换句话说,这些球体看起来像杂货店里橙子的金字塔形堆叠。)
但是,如果我们只考虑有限数量的球体,情况就大不相同了。 现在我们又回到了用包装纸包裹橙子的例子。 如果你只有一个或两个橙子,那么如何最佳地排列它们就一目了然了。 如果你有三个,任务就更复杂了。 你可以将它们排成一排(香肠包装)或像以前一样用它们形成一个三角形(披萨包装)。 情况类似于三个硬币的情况,只是你处理的是球体。 为了找出在这种情况下哪种包装最节省空间,你可以比较排列的体积。
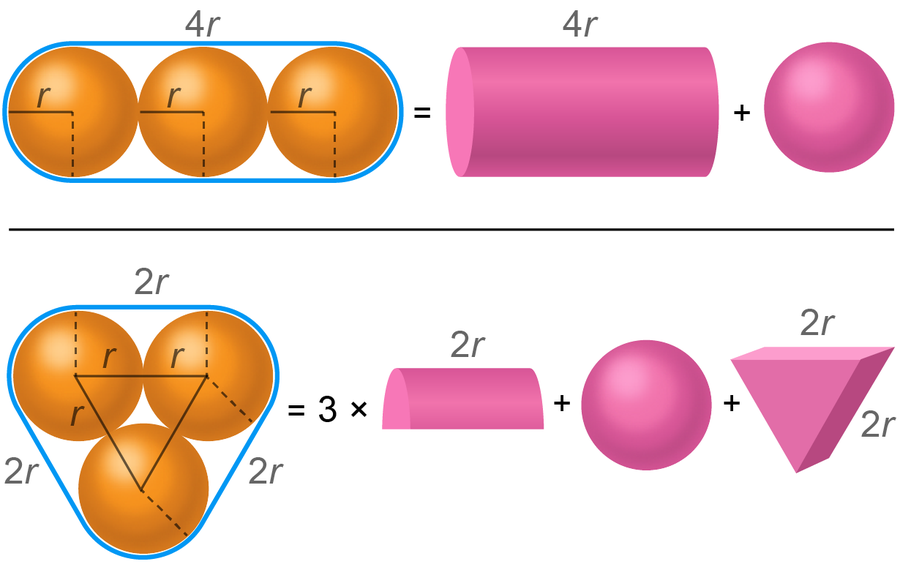
为了找到包装三个球体的最佳方法,你必须计算每种情况下的体积。 来源: Spektrum der Wissenschaft/马农·比肖夫,由 大众科学 设计风格
为了开始,它有助于再次将球体的外壳分解为单个几何形状,并将它们的体积相加。 在香肠包装的情况下,这非常简单: 形状可以分为一个圆柱体和一个球体,它们的总体积为 16⁄3π r3 ≈ 16.76r3。 披萨包装有点复杂。 你得到三个半圆柱体、一个三角棱柱和一个球体,它们的总体积为 13⁄3πr3 + 2√ 3r3 ≈ 17.08r3。 因此,在这种情况下,香肠包装更节省空间。 事实证明,香肠排列确实可以最佳地包装。
香肠灾难
如果你再添加一个球体,使 n = 4,你可以区分三种不同的排列方式。 同样,你可以将球或橙子一个接一个地排成一行(香肠),或者将它们分布在平面上(披萨)。 但是你也可以使用所有三个空间维度并堆叠它们,这种排列方式称为“簇”包装。 即使对于四个球,也可以证明香肠包装是最优的,因为它需要的体积最小。
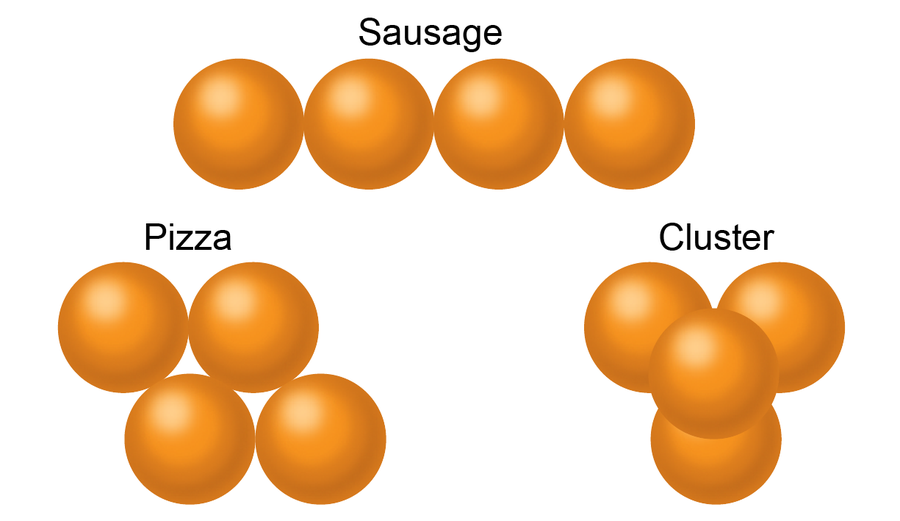
三种可能的包装排列方式。 来源: Spektrum der Wissenschaft/马农·比肖夫,由 大众科学 设计风格
然而,随着球体数量的增加,事情变得更加复杂。 数学家们推测,香肠包装对于最多 n = 55 个球是最优的。 但在 1992 年,数学家约尔格·威尔斯和皮尔·马里奥·甘迪尼确定,对于 56 个球,簇包装更节省空间。 然而,这个簇到底是什么样子尚不清楚。 数学家们能够找到比球的香肠包装更好的排列方式——但无法证明它是最优的。 可能存在另一种占用更少体积的排列方式。
从有序的一维链到三维簇的突然转变在专家圈内被称为“香肠灾难”。 威尔斯和甘迪尼证明,对于 59、60、61 或 62 个球体的排列,以及所有至少包含 65 个球的集合,也最优地形成一个簇。 对于所有其他数量——也就是说,当 n 小于 56 或为 57、58、63 或 64 时——香肠包装似乎是最优的。 这意味着,对于最多 55 个球,香肠包装可能是最优的,对于 56 个球,簇包装是最佳的,而对于 57 或 58 个球,香肠包装将再次是最节省空间的排列方式。 对于 59、60 或 61 个球体,我们又回到了簇包装。
这个答案似乎并不特别直观。 并且没有人能够毫无疑问地证明这一点。
访问 42 维空间
如果数学家们止步于三维,他们就不会成为数学家了。 那么,n 个四维球体在四维空间中的最佳包装是什么样的呢? 在更高维度中,表示为 d,,区分香肠包装(一维链)、簇包装(整个 d 维空间中球体的累积)和披萨包装。 后者代表了其他两种情况的一种过渡: 它包括球体分布在超过一个维度且小于 d 维度的所有情况。
事实证明,在四维空间中似乎也存在香肠灾难,尽管它发生的比三维情况晚得多。 甘迪尼和他的同事安德烈亚娜·祖科在 1992 年证明,在 d = 4 中,一旦你拥有至少 n = 375,769 个球,簇包装比香肠包装更节省空间。
那么披萨呢? 威尔斯和数学家乌尔里希·贝特克和彼得·格里茨曼在 1982 年表明,披萨在三维和四维空间中永远不是最佳包装。 球体要么填充整个空间(簇),要么形成一条线(香肠)。 只有这两种极端情况才能产生最佳包装排列。
1975 年,费耶斯·托特表达了他现在著名的针对更高维度的“香肠猜想”。 根据他的说法,香肠包装对于五维或更高维度中的任何有限数量的球体都是最优的。 即使这个猜想尚未得到最终证明,贝特克和他的同事马丁·亨克在 1998 年能够证明,香肠猜想适用于42 个或更多空间维度。
简而言之,如果你要赠送 42 维橙子作为圣诞礼物,最好将它们排成一排。 并且,如果像最初的问题一样,你只是赠送五个这样的三维水果,那么香肠式包装将是完美的。
现在想象一下,当你不想包装橙子而是恐龙玩具或娃娃时,任务变得多么复杂。 礼品包装显然是一个充满数学谜题的领域。
本文最初发表于《明镜周刊》 并经许可转载。
