不公正划区正在全国各地的法庭和头条新闻中蔓延。美国最高法院最近听取了关于威斯康星州共和党和马里兰州民主党选区合宪性的案件,这些选区据称巩固了他们的强大优势,但在两起案件中都避开了直接裁决。北卡罗来纳州的另一起党派不公正划区案件正在上诉中,8月份下级法院的一份措辞强烈的意见书推动了该案件的进展。但到目前为止,要让大法官们对党派不公正划区的法律框架感到满意一直是不可能的。正如前大法官安东尼·肯尼迪在2004年的一起案件中指出的那样,部分问题在于,高等法院和下级法院尚未就“可行的标准”来确定什么是党派不公正划区达成一致。这就是全国越来越多的数学家认为我们能够提供帮助的地方。
两年前,我和几个朋友成立了一个工作组,研究几何学和计算在美國重新劃分選區中的应用。从那时起,“度量几何与不公正划区小组”扩大了其范围和使命,深入参与研究、推广、培训和咨询。全国各地有超过1200人参加了我们的研讨会,他们中的许多人已经深入参与到重新劃分選區项目中。我们认为现在是时候进行计算干预了。不公正划区的数学原理出人意料地丰富——足以开创一个独立的子领域——而计算能力可以说才刚刚赶上重新劃分選區问题的规模和复杂性。尽管我们小组的技术导向,但我们的中心目标是加强和保护公民权利,我们正在与律师、政治学家、地理学家和社区团体密切合作,在下一次美国人口普查和随后的重新劃分選區之前建立工具和想法。
在一个权力掌握在民选代表手中的国家,对于选举过程的控制权总是会存在冲突。在像我们众议院这样的制度中——每个地理选区内胜者全得——选区的划分是一个天然的战场。美国历史上充斥着令人震惊的划线计划,从在一个选区塞满现任议员的忠实拥护者,到将一个历史悠久的选区切成三块,以压制黑人选民的政治权力。许多种类的所谓“集中”和“分散”策略至今仍在继续,在大数据时代,它们变得异常复杂。现在,比以往任何时候都更难明确地识别出滥用重新劃分選區的行为。人们认为他们通过两个特征来了解不公正划区——怪异的形状和不成比例的选举结果——但两者都不可靠。那么,我们如何确定天平何时被不公平地倾斜了呢?
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和想法的具有影响力的故事的未来。
眼球测试
1812年的事件赋予了我们“不公正划区”这个词,它源于这样一种直觉,即形状怪异的选区会暴露不合法的意图。它以当时的马萨诸塞州州长埃尔布里奇·格里命名。格里拥有相当显赫的开国元勋血统——《独立宣言》的签署人、美国制宪会议的主要参与者、国会议员、詹姆斯·麦迪逊的副总统——因此,考虑到他永恒的名声来自于不正当的重新劃分選區,这很有趣。“格里-曼德”,或格里的蝾螈,是给波士顿北岸一个弯曲的选区的讽刺性名称,人们认为这个选区有利于州长的民主共和党,而不利于竞争对手联邦党人。《塞勒姆公报》在1813年刊登了一幅木刻政治漫画;漫画中,翅膀、爪子和毒牙被暗示性地添加到选区的轮廓中,以增强其爬行动物般扭曲的外观。
因此,不规则的选区会暗示我们存在不当行为的观点由来已久,而紧凑的选区促进民主理想的观念也与共和国一样古老。1787年,麦迪逊在《联邦党人文集》中写道,“民主的自然限制是距离中心点的距离,这个距离刚好允许最偏远的公民尽可能频繁地聚集,以履行他们的公共职能。”换句话说,选区应该是可通行的。1901年,一项联邦分配法案首次在美国法律中出现了“选区应由‘紧凑的领土’组成”这一模糊的要求。“紧凑”一词随后在重新劃分選區的法律领域中激增,但几乎总是没有定义。
例如,在2017年举行的全国州议会会议上,我了解到,在上一次人口普查之后,犹他州的立法者花了值得称赞的时间和精力建立了一个名为“重新劃分選區犹他州”的网站,向普通公民征集提议的选区地图。为了被考虑,地图必须“合理紧凑”。我抓住机会想弄清楚这个质量是如何被测试和执行的,结果却得知它只是通过抛弃那些看起来滑稽的地图来处理的。如果这听起来很糟糕,那么犹他州绝非孤例。三十七个州对地图形状制定了一些规定,几乎在所有情况下,眼球测试都是最重要的。
问题在于,选区的轮廓讲述的是一个非常片面且常常具有误导性的故事。一方面,形状难看肯定有良性的原因。自然地理或合理地尝试遵循县界或联合利益社区可能会影响边界,尽管同样常见的是,这些合法的优先事项仅仅是被当作替罪羊,试图为最令人反感的选区辩护。另一方面,圆润、矮胖和对称的选区并不能提供有意义的质量保证。就在今年,宾夕法尼亚州共和党在州议会起草的一项国会重新劃分選區计划在宾夕法尼亚州最高法院规定的所有五种公式下都取得了很高的紧凑性得分。然而,数学分析显示,该计划仍然会锁定与2011年制定的扭曲计划相同的极端党派偏见,该计划旨在取代2011年的计划。因此,法官们选择了采取非常措施,采纳了一项独立的外部人员的计划。
失衡的结果
如果形状不是不公正划区的可靠指标,那么研究民选代表与选民投票模式的匹配程度又如何呢?当然,失衡的结果提供了初步的滥用证据。但别急。以我在家乡马萨诸塞州的共和党人为例。自2000年以来,在13次联邦总统和参议院选举中,共和党候选人在全州范围内平均获得了超过三分之一的选票。这比在马萨诸塞州九个国会选区之一中赢得席位所需的水平高出六倍,因为在两方竞争中,候选人需要获得简单多数才能获胜。然而,自1994年以来,没有共和党人在众议院赢得席位。
我们一定看到了一个不公正划区,它剥夺了共和党人理应获得的席位,对吗?但这里的数学完全是开脱罪责的。让我们看看全州范围内的竞选,这样我们就可以把无人竞争的席位和其他混淆变量放在一边。以肯尼斯·蔡斯为例,他是2006年美国参议院泰德·肯尼迪的共和党挑战者,他获得了全州范围内30%以上的选票。按比例计算,你可能会期望蔡斯在九个国会选区中的近三个选区击败肯尼迪。但数字并不符合。事实证明,在州内选择一个单一的、选区大小的城镇或选区分组(即使分散在全州各地)来偏爱蔡斯在数学上是不可能的。他的选民根本不够集中。相反,大多数选区对蔡斯的支持率接近州平均水平,因此没有足够的偏爱蔡斯的组成部分来分配。
任何投票少数派都需要一定程度的非均匀性,才能使其选票分布符合我们的选区劃分選區系统,以便为获得代表权提供哪怕是理论上的机会。应用于蔡斯-肯尼迪竞选的分析甚至没有考虑空间因素,例如每个选区必须是一个连通整体的标准要求。人们可能会理所当然地怀疑,当各种可能性的前景会带来如此多的惊喜时,我们如何才能追究选区设计师的责任。
随机游走来救援
评估一个选区劃分選區计划的公正性的唯一合理方法是将其与切割同一管辖区的其他有效计划进行比较,因为您必须控制选举结果的各个方面,这些方面是州法律、人口统计和地理因素强制造成的。问题在于,研究可能的计划宇宙变成了一个难解的大问题。
想象一个简单的四乘四的网格,假设你想把它分成四个大小相等的连续选区,每个选区有四个正方形。如果我们把网格想象成棋盘的一部分,我们把连续性解释为车可以在整个选区内访问,那么恰好有117种方法可以做到这一点。如果允许角相邻——所谓的后翼连续性——那么就有2620种方法。而且它们并不那么容易计数。正如我的同事、马萨诸塞大学洛厄尔分校的教授、组合枚举领域的领导者吉姆·普罗普所说,“在一维中,你可以沿着路径分割来分而治之,但在二维中,突然之间就有很多很多种从A点到B点的方法。”
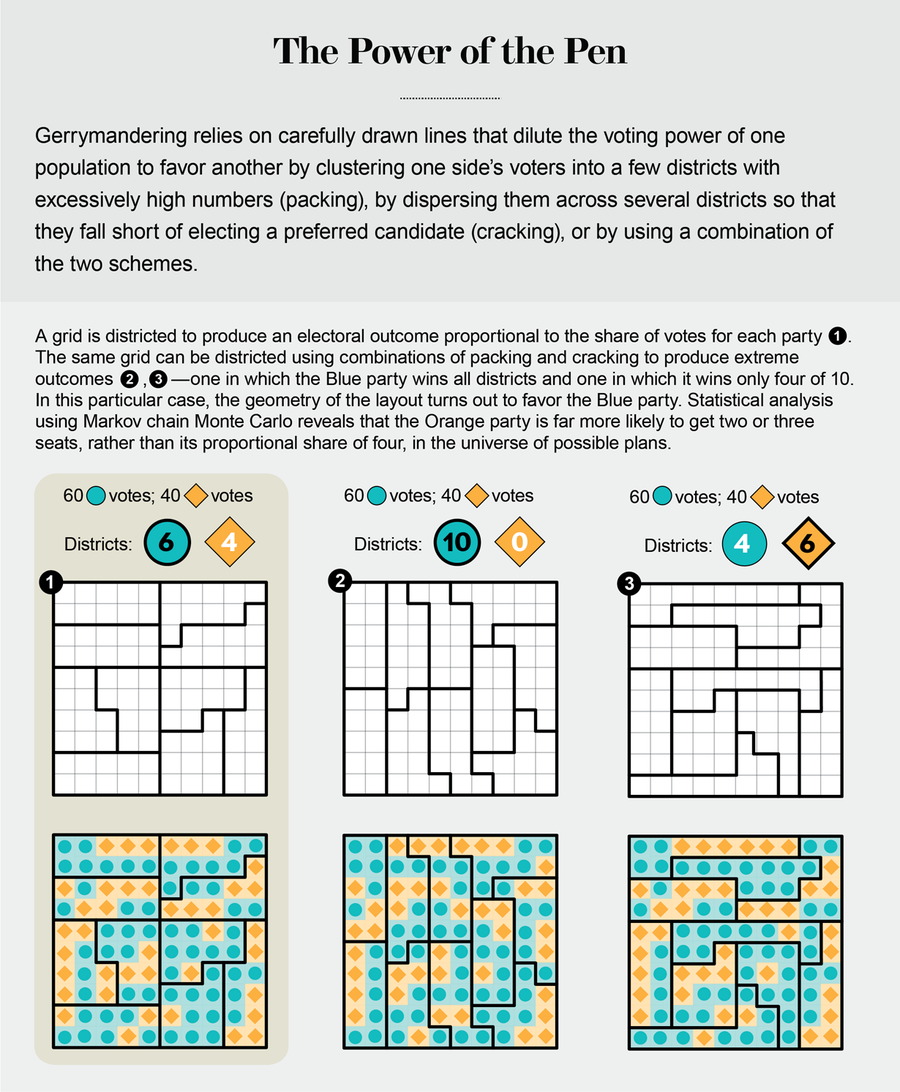
信用:詹·克里斯蒂安森
问题在于,最好的计数技术通常依赖于递归——也就是说,使用一个类似的、规模小一步的问题来解决问题——但是二维空间计数问题在没有一些额外的结构的情况下,递归效果不佳。因此,完整的枚举必须依赖于蛮力。虽然一台巧妙编程的笔记本电脑几乎可以立即对小网格的分区进行分类,但随着网格尺寸的增长,我们看到了复杂性的巨大飞跃,这项任务很快就变得遥不可及。当您到达九乘九的网格时,等数车的分区有超过700万亿个解,即使是高性能计算机也需要一周的时间才能将它们全部计数。这看起来像是绝望的境地。我们试图评估一种切割州的方式,但没有任何能力来枚举——更不用说有意义地将其与——替代方案的宇宙进行比较。这种情况听起来像是在黑暗、无限的荒野中摸索。
好消息是,在科学领域中,有一个行业标准用于处理如此庞大的任务:马尔可夫链蒙特卡罗(MCMC)。马尔可夫链是随机游走,其中下一步的去向由概率控制,仅取决于您现在的位置(在每个位置,您掷骰子选择一个相邻空间移动)。蒙特卡罗方法只是通过随机抽样进行估计。将它们放在一起,您就得到一个强大的工具,用于搜索广阔的可能性空间。MCMC已成功用于解码监狱信息、探测液体的性质和相变、为困难的计算问题找到可证明准确的快速近似值等等。著名统计学家珀西·戴康尼斯在2009年的一项调查中估计,MCMC推动了科学、工程和商业领域10%到15%的统计工作,而且这个数字可能只会从那时起上升。尽管重新劃分選區中的计算分析可以追溯到几十年前,但认真尝试将MCMC应用于这项工作直到2014年左右才开始公开出现。
.png?w=900)
信用:詹·克里斯蒂安森;来源:扎卡里·I·舒茨曼和弗洛尔·范德维尔德
假设网格兰州的官员聘请您来决定他们立法机构的选区劃分選區计划是否合理。如果网格兰州是一个四乘四的正方形网格,并且其州宪法要求车连续选区,那么您就走运了:恰好有117种方法可以生成符合要求的计划,您可以检查所有这些计划。您可以使用117个节点来表示有效的计划,并在节点之间添加边来表示简单的移动,其中网格中的两个正方形交换其选区分配,从而建立这个选区劃分選區计划宇宙的完美忠实模型。这些边为您提供了一种概念化两个计划有多相似的方法,只需计算将一个计划转换为另一个计划所需的交换次数。(我将这种结构称为“元图”,因为它是一个切割另一个图的方式的图。)现在假设州立法机构由钻石党控制,其竞争对手怀疑它已经操纵了席位以支持自己。为了确定这是否属实,可以求助于选举数据。如果钻石计划在上次选举中为该党产生的席位比方说117个备选方案中的114个更多,并且在之前的几次选举中也是如此,那么该计划显然是一个统计异常值。这是党派不公正划区的有力证据——而您不需要MCMC来进行这样的分析。
当您遇到一个完整规模的问题来代替这个小型玩具问题时,MCMC方法就会发挥作用。一旦您超过100个左右的节点,就会出现一个类似的元图,但您无法完全构建它,因为它具有令人望而生畏的复杂性。但这并不是什么大问题。从任何一个计划来看,通过执行所有可能的移动来构建局部邻域仍然很容易。现在您可以走一百万步、十亿步或万亿步,看看您发现了什么。背景中有数学原理(确切地说,是遍历理论)保证,如果您随机游走足够长的时间,您收集的地图集合将具有代表总体宇宙的属性,通常在您甚至访问过州空间中一小部分节点之前很久。这使您可以确定您正在评估的地图是否是根据各种党派指标的极端异常值。
科学探索的前沿是构建更强大的算法,同时设计新的定理来证明我们的抽样足够好,可以得出可靠的结论。围绕这种方法正在形成一种新兴的科学共识,但也存在许多正在进行的研究方向。
R.I.P. 格里州长
到目前为止,法院似乎对这种方法表示赞许。杜克大学的乔纳森·马廷利和卡内基梅隆大学的韦斯·佩格登两位数学家最近分别就北卡罗来纳州的联邦案件和宾夕法尼亚州的州级案件的MCMC方法作证。
马廷利使用MCMC来描述人们可能在各种选区劃分選區计划集合中观察到的各种指标(例如赢得的席位)的合理范围。他的随机游走被加权,以偏爱那些被认为更接近理想的计划,这与北卡罗来纳州法律的思路一致。利用他的集合,他认为已颁布的计划是一个极端的党派异常值。佩格登使用了一种不同类型的测试,借鉴了一个严格的定理,该定理量化了一个中立计划的得分比随机游走访问的其他计划差得多的可能性有多小。他的方法产生p值,这限制了偶然发现这种异常偏差的可能性有多大。法官们认为这两种论点都是可信的,并在各自的判决中赞赏地引用了它们。
就我而言,宾夕法尼亚州州长汤姆·沃尔夫今年早些时候聘请我担任咨询专家,为该州在其最高法院决定推翻2011年共和党计划后,争先恐后地划定新的选区界限。我的贡献是使用MCMC框架来评估提出的新计划,利用统计异常值的力量,同时增加新的方法来考虑更多的各种选区劃分選區原则,从紧凑性到县分割再到社区结构。我的分析与佩格登的分析一致,都将2011年的计划标记为极端的党派异常值——我发现州立法机构提出的新计划也同样极端,而其外观的改善并不能解释这一点。
随着2020年人口普查的临近,全国正在为新一轮疯狂的重新劃分選區做好准备,随之而来的是诉讼的承诺。我希望接下来的步骤不仅会在法庭上进行,也会在改革措施中进行,这些措施要求在使用开源工具制作的大量地图被审查后,才能签署任何计划成为法律。这样,立法机构保留了他们委托和批准选区边界的传统特权,但他们必须提供一些保证,确保他们不会在天平上放上太重的砝码。
计算永远不会为我们做出艰难的重新劃分選區决定,也无法产生最优的公平计划。但它可以证明一个计划的行为就像是从既定的规则中选择出来的一样。仅此一点就可以控制最恶劣的滥用行为,并开始恢复对系统的信任。
*编者注(10/23/18):由于数据变化,表格“如何比较无数的选区劃分選區计划”的中间和右列中的一些数字在发布后进行了调整,与11月印刷版《大众科学》中出现的版本不同。

