数学爱好者的福利：生命游戏创造者约翰·康威的一些谜题

2020 年 4 月 11 日，约翰·霍顿·康威因新冠肺炎在新泽西州新不伦瑞克去世，享年 82 岁。这位杰出的数学家研究领域包括群论、纽结理论、几何学、分析学、组合博弈论、代数学、算法学，甚至理论物理学。

康威的兴趣和天赋使他发明了一种名为“生命游戏”的非凡的细胞自动机，在 50 年后仍然令人着迷。康威还设计了精巧的谜题，用于包装只能通过巧妙的推理才能有效解决的积木盒。

康威认为，他最重要的贡献是对一个

关于支持科学新闻报道

如果您喜欢这篇文章，请考虑支持我们屡获殊荣的新闻报道，方式是 订阅。通过购买订阅，您将帮助确保未来能够继续推出关于塑造当今世界的发现和想法的具有影响力的报道。

被称为超现实数的奇妙数字系统的概念化。这个类别包括整数、实数、超限数和无穷小——这是一个以前没有人想象过可能存在的结构，其中一切都可以相加、相乘等等。

与康威共事过的人报告说，他思维非常敏捷，以至于他刚听到一个问题，往往就已经有了解决方案。康威对面向所有人的数学的执着，促使他研究令休闲数学爱好者感到愉悦的谜题，例如著名的考拉兹猜想（本文末尾将讨论该猜想）。

康威是在我的《科学》杂志法语版《Pour la Science》专栏中被引用次数最多的数学家（超过 30 次！）。在准备文章时，我经常会遇到他证明的结果或他在该主题上率先提出的重要想法，这让我非常惊讶。康威喜欢简单、实用的数学问题，这些问题需要发挥他的创造力。

在我看来，纪念他的最好方式是突出那些让他惊叹和着迷的数学。我将介绍康威做出贡献的几个不同主题。但是，要充分展现这位非凡的思想家的才华，需要写几卷书才行。他能够在许多不同的领域发明物体和问题，并解决最棘手的难题，构思出无人能想到的方法。

√2 的无理数性

最令人惊讶和重要的数学发现之一是 2 的平方根 (√2) 的无理数性——边长为 1 个单位的正方形的对角线的长度。 它不能用正整数 n 和 m, 的商或 n/m 来表示。√2 的无理数性的发现归功于毕达哥拉斯或他的弟子之一，尽管我们不知道其背后的推理是算术的还是几何的。这一发现及其证明对数学家来说是极其令人不安的。数学中的第一个负面发现表明，人类并没有创造支配数字的定律，而是在探索未知的数学领域时揭示了这些定律。

尽管有许多定理证明，但最直观的是康威在 2005 年出版的一本书中的讲座中包含的一个非常简单的简图。  他将这个证明的创建归功于数学家斯坦利·泰嫩鲍姆，据康威说，他已经放弃了数学。您可能会问，这个证明是否是康威自己提出的。但这并不重要。因为即使不是他创造的，这个证明也完美地体现了康威的数学方法，他在 100 种不同的方式中都展示了这种方法。它还表明，认为一切简单的事物都已被发现是错误的：辉煌而又出奇简单的想法仍在等待被揭示。

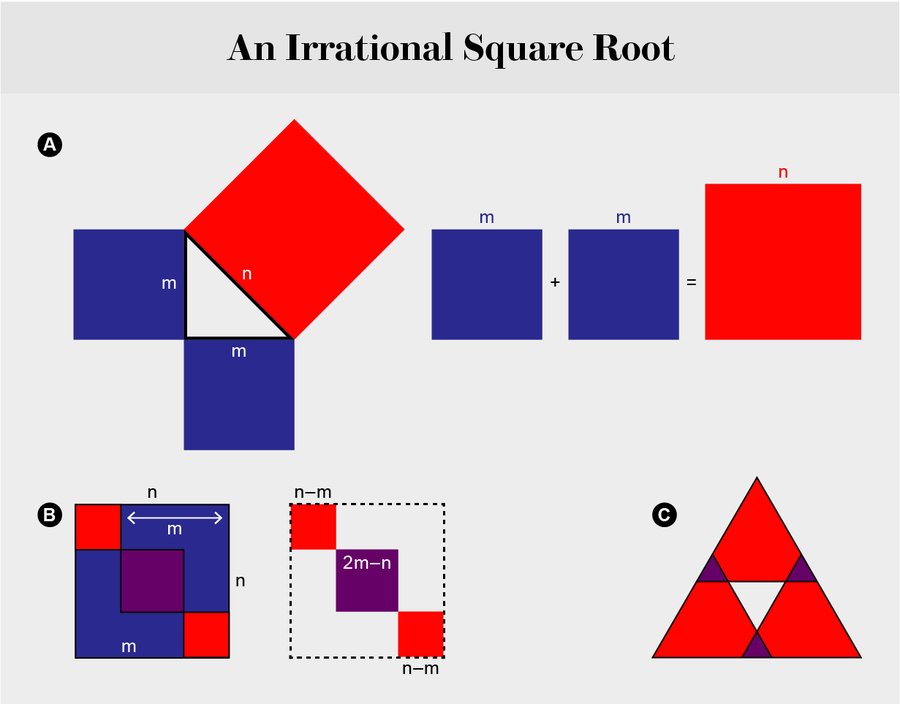
假设 √2 是 n 和 m 的商——也就是说，2 = n²/m², 或 2m² = n²。如果是这样，则存在一个边长等于 n 的正方形，其面积等于边长等于 m 的正方形的两倍 [参见“无理平方根”的 A 部分]。我们假设在我们的图中，m 是满足此方程的最小正整数。只有在没有更小的正整数满足它时，该假设才有效。

将两个蓝色正方形楔入红色正方形的两个对角角落会产生一个新的形状。该形状中的两个红色正方形的面积必须与两个蓝色正方形重叠处创建的中心紫色正方形的面积相同 [参见“无理平方根”的 B 部分]。

我们的推理要求两个蓝色正方形的面积必须等于红色正方形的面积 (A)。因此，未被两个蓝色正方形覆盖的面积等于两者覆盖的面积的两倍。换句话说，有两个相等且较小的正方形（红色，B），它们加在一起的面积与较大的正方形（紫色，B）相同。这意味着新的小正方形的每条边都等于整数 n – m，而大的紫色正方形的每条边都等于整数 n – 2(n – m) = 2m – n。

简而言之，边长为 m 的初始正方形不是满足几何方程的最小正方形。结果是一个矛盾，因此假设是错误的：√2 不是两个整数的商，这意味着它是一个无理数。以同样的方式，您可以证明 3 的平方根是无理数 [参见“无理平方根”的 C 部分]。

三个立方体堆叠谜题

许多谜题包括将少量积木放入盒子中（例如 10 个）。积木和盒子通常都是长方体。解决方案通常是通过反复试验得出的。对于这样的问题，除非您增加积木的数量及其形状的多样性，否则很难构思出一个具有挑战性的谜题。此外，尽管在找到解决方案之前操作积木可能很有趣，但这样做只涉及到对形状的少量推理，因此并没有真正减少解决时间。

康威重新构想了这个问题，创造了可能会让您在尝试找出如何填充盒子时陷入循环的谜题。但是，一些精明而有条不紊的考虑将很快引导您找到解决方案。

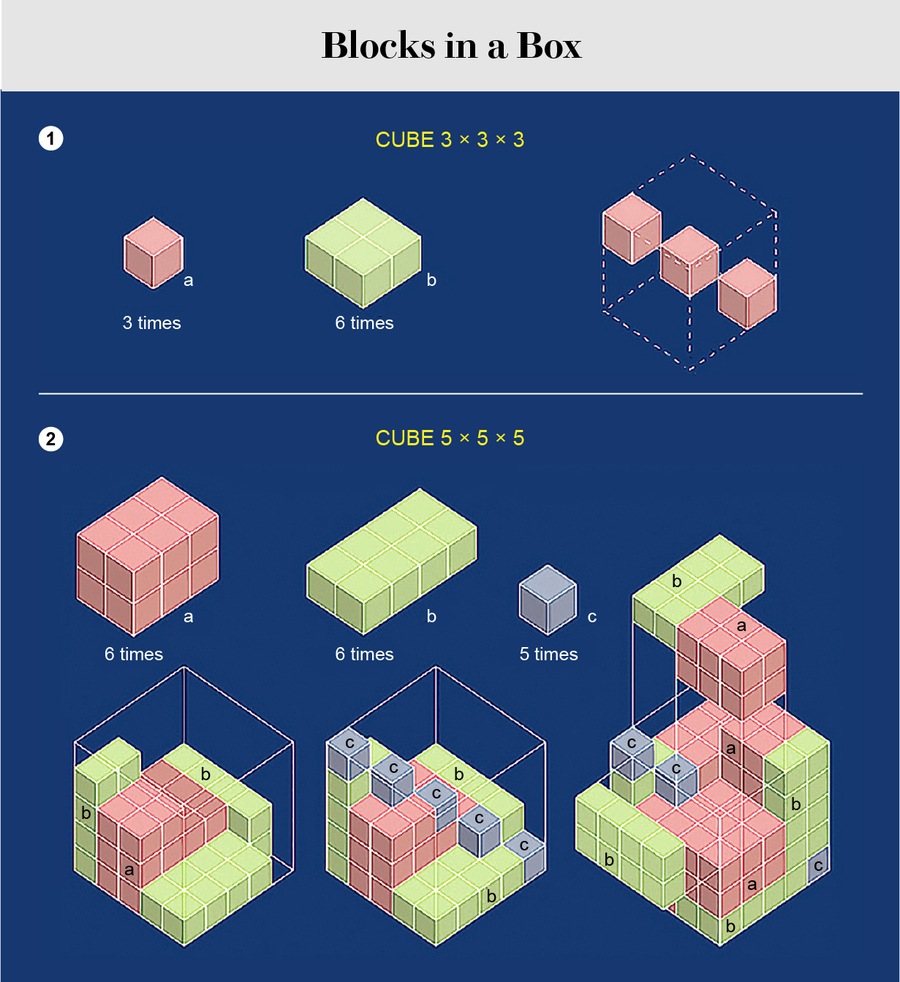
这三个谜题中最简单的一个是用三个 1 x 1 x 1 的立方体和六个 1 x 2 x 2 的长方体填充一个 3 x 3 x 3 的盒子 [参见“盒子里的积木”的第 1 部分]。

推理包括考虑奇偶性：3 x 3 x 3 的盒子由三个水平的 3 x 3 x 1 层组成，每层的体积为 9。3 x 3 x 3 的盒子也可以分解为三个垂直的 3 x 3 x 1 长方体，每个长方体平行于盒子的一个垂直面。考虑垂直面产生盒子分解为三个 3 x 3 x 1 长方体的第三种分解方式。

让我们检查一下这九个长方体。当一个 1 x 2 x 2 的积木放置在盒子中时，它只能填充每个 3 x 3 x 1 层中九个单元格的偶数个。因此，每一层都必须包含三个小的 1 x 1 x 1 积木中的一个——且仅一个——（否则您必须将所有三个都放在一个 3 x 3 x 1 层中，这将导致其他两层中没有，而它们是需要的）。因此，盒子的顶层必须包含一个 1 x 1 x 1 的积木。如果我们将它放在该层的中心，我们很快就会陷入僵局，因为我们不得不将另一个小积木放在它的正下方。这将它们中的两个放在一个 3 x 3 x 1 的垂直层中。将顶面上的小积木放在任何一侧的中间也会导致僵局。因此，顶层上的小积木必须放在一个角上。

同样的推理适用于底层，底层上的小积木也必须放在一个角上。那个角必须与顶层上的小积木对角相对。因此，第三个小积木必须放在中间层的中心。剩下的步骤很快就变得显而易见了。请注意，这种推理不仅产生了解决方案，而且还表明，除了对称性之外，只有一个解决方案。

康威的另一个堆叠问题（“盒子里的积木”的第 2 部分）中显示了解决方案。要完成堆叠，您只需降低两个上部结构，并将绿色层 (b) 放在粉色层 (a) 上方的侧面即可。基于奇偶性的推理迫使我们将单位立方体沿对角线放置。

两个巫师的谜题

在 20 世纪 60 年代，康威设计了一个极其棘手的谜题，直到最近，该谜题还引发了许多争论，并且麻省理工学院的塔尼娅·霍瓦诺娃在 2013 年发表了一篇论文。以下是该论文中出现的谜题

昨晚我坐在公共汽车上的两位巫师后面，无意中听到以下对话

巫师 A：“我有几个正整数个孩子，他们的年龄都是正整数，他们的年龄之和是这辆公共汽车的号码，而他们的年龄之积就是我的年龄。”

巫师 B：“真有趣！也许如果您告诉我您的年龄和孩子的数量，我可以算出他们每个人的年龄？”

巫师 A：“不。”

巫师 B：“啊哈！我终于知道您多大了！”

那么，公共汽车的号码是多少？

请注意，在对话中，巫师 A 说的“不”并不意味着他拒绝回答，而是意味着知道他的年龄和孩子的数量并不能知道他们每个人的年龄。当然，您必须假设巫师 B 知道公共汽车的号码。还要注意，巫师可能非常年轻或非常年老：巫师 A 很可能只有两岁或两万岁。

这是解决方案，我只能在程序的帮助下完全理解和验证它。我无法重现得出结论所需的所有计算，但您可以相信我的话，或者重新进行我遗漏的所有计算。

让我们将巫师 A 的年龄表示为 a，公共汽车的号码表示为 b，巫师 A 的孩子的数量表示为 c。例如，假设公共汽车的号码是 b = 5。以下是孩子数量、年龄分布和巫师 A 年龄的选项

• c = 5 个孩子，年龄分别为 1、1、1、1、1；因此，a = 1；

• c = 4 个孩子，年龄分别为 1、1、1、2；因此，a = 2；

• c = 3 个孩子，年龄分别为 1、1、3；因此，a = 3；

• c = 3 个孩子，年龄分别为 1、2、2；因此，a = 4；

• c = 2 个孩子，年龄分别为 1、4；因此，a = 4；

• c = 2 个孩子，年龄分别为 2、3；因此，a = 6；

• c = 1 个孩子，年龄为 5；因此，a = 5。

在每种情况下，知道巫师 A 的年龄和孩子的数量都可以指示后者的可能年龄。由于巫师 A 回答“不”，并且巫师 B 知道公共汽车的号码，这意味着 b 不等于 5。

同样，您可以通过逐个检查可能的公共汽车号码来解决问题，以找到那些知道巫师的年龄和孩子的数量也不能让您知道每个孩子的年龄的号码（我们将其表示为属性 P）。计算 b = 1、2、3、...、12（正如我们刚刚对 b = 5 所做的那样）表明，b = 12 是具有属性 P 的最小数字。

实际上，对于 b = 12 和 c = 4，有两组可能的四个孩子的年龄——(2, 2, 2, 6) 和 (1, 3, 4, 4)——它们都给出了相同的巫师 A 年龄：a = 48。对于 b = 12，不存在其他两个长度相同且乘积相同的集合。因此，对于 b = 12，即使知道 c = 4 和 a = 48，也不可能推断出四个孩子的年龄。这是否意味着 b = 12 是解决方案？

不幸的是，还不是。例如，对于公共汽车号码 b = 13，因为两组可能的三个孩子的年龄——(1, 6, 6) 和 (2, 2, 9)——都与 a = 36 兼容，巫师 B 无法从知道他的年龄或孩子的数量中推导出巫师 A 的孩子的年龄。

知道 b = 12 并不比知道 b = 13 更能确定孩子的年龄。当面对这个谜题时，大多数人通常会回答“b = 12”，就好像这个谜题以某种方式暗示最小可能的 b 解决方案是正确的解决方案。但是，该谜题并没有做出这样的断言。此外，如果没有进一步的推理，您无法在 b = 12 和 b = 13 之间做出选择，也无法在其他 b 值之间做出选择，正如我的进一步计算表明的那样。

然而，b = 12 是正确的答案，而原因在于谜题中最有趣和最出乎意料的部分。康威精心设计了他的谜题，您必须考虑巫师 B 的最后陈述。在巫师 A 说“不”之后，巫师 B 回答说：“啊哈！我终于知道您多大了！” 这排除了 b = 13。

事实上，对于 b = 13，还有另外两组孩子的年龄——(1, 2, 2, 2, 6) 和 (1, 1, 3, 4, 4)——它们都给出了 a = 48。换句话说，如果公共汽车号码是 13，巫师 B 就无法从他的否定回答中推断出巫师 A 的年龄，因为他的年龄可能是 36 或 48。因此，应该排除 b = 13。

然而，排除 b = 13 会导致排除 b = 14，当我们考虑为 b = 13 找到的年龄序列并加 1 时。这样做表明，两组孩子的年龄——(1, 1, 6, 6) 和 (1, 2, 2, 9)——的乘积是 a = 36，而另外两组——(1, 1, 2, 2, 6) 和 (1, 1, 1, 3, 4, 4)——的乘积是 a = 48。相同的过程排除了 b = 15，并逐个排除了所有大于 12 的 b。

因此，只有公共汽车号码 12 (b = 12)，以及两组孩子的年龄——(2, 2, 2, 6) 和 (1, 3, 4, 4)——才能唯一确定巫师 A 的年龄：a = 48。

鉴于您必须进行所有计算才能得出解决方案——我在这里没有重现这些细节，而且这些细节占据了几个页面——我承认我不明白康威是如何构思出这个令人难以置信的谜题的！

用线段铺满平面

用正方形铺满平面很容易。用等边三角形或六边形这样做也很容易。也可以用无限条直线铺满平面：只需将它们并排平行放置即可。将有无数条直线，但铺满效果将非常令人满意，因为平面的每个点都将属于铺满线中的一条——且仅一条。以下是一些更棘手的问题

• 平面可以用闭合线段铺满吗？即包括端点的直线线段 [A, B]？

• 平面可以用开放线段铺满吗？即不包括端点的线段 ]A, B[？

• 平面可以用半开放线段铺满吗？即仅包含一个端点的线段 ]A, B]？

思考一下这些不寻常但又完全自然的问题。它们并非如此简单。康威和一位同事在 1964 年发表的一篇精彩论文中讨论了这些问题和其他类型的问题，再次证明了没有人思考过的非常简单的问题是进行不太明显的数学运算的绝佳机会。

在该论文中，康威和数学家哈拉德·克罗夫特设计了一种用直线线段填充平面的方法，这可以在下面的“精细铺路”中看到。

面板 a 显示了如何用半开放线段铺满平面，其中包含一个点，而另一个点被排除在外。这样做很容易，因为将它们首尾相连地放置在一起，就可以重现用直线进行的明显铺路。

面板 b 显示了相等闭合线段的解决方案，其中每个线段的两个点都包含在内。首先放置支柱 1。然后添加支柱 2，但当然不保留此堆栈的最左侧线段。对于支柱 3，不保留最右侧线段。连续添加越来越精细的倾斜支柱，省略每个支柱的“第一个”线段。

面板 c 显示了不同尺寸的开放线段（其端点被排除在外）的解决方案。这些线段创建了一个中心正方形，该正方形在所有侧面都是开放的——即，正方形的边和顶部或底部都没有被覆盖。每个连续添加的矩形也是开放的。对于相同长度的开放线段，没有铺满平面的解决方案。

考拉兹猜想

另一个谜题对于业余数学家和专业人士都同样有趣。考虑一个函数 (f)，该函数对于正偶数整数 (n) 给出 n/2，对于正奇数整数 (n) 给出 3n + 1。例如，从 7 开始并应用 f，您得到 22，然后是 11、34、17、52、26、13、40、20、10、5、16、8、4、2、1、4、2、1，依此类推。一旦您到达 1，您就会绕圈打转。

无论您从哪个整数 n 开始，您似乎总是最终到达 1，然后陷入循环。 计算机计算已经测试了此属性，对于至少高达 87 x 2⁶⁰（约 10²⁰）的所有 n 都为真。然而，尚未证明情况总是如此，也未找到会继续延伸到无穷大或导致 4、2、1 以外的循环的初始 n。

这个问题被称为考拉兹猜想或锡拉丘兹猜想。已经投入了大量工作来研究它，其中一些工作已汇编成一本书。该问题陈述的极大简洁性吸引了业余爱好者，我经常收到提出的解决方案，但迄今为止，这些解决方案要么是错误的，要么是无法理解的。

面对这样一个挑战——如此简单地陈述但尚未解决，80 多年后仍然如此——康威无法抗拒。

1972 年，他发表了关于该主题的第一篇论文，其中他提出了类似表述的问题，并证明了它们的不可判定性。对于起始整数的某些值，由 f 的变体生成的序列不会最终到达 1，但集合论无法证明这一点。更一般地，对于任何逻辑证明系统 (S)，都存在此类别的问题以及一个序列的起点，该序列不会最终到达 1，而这无法被 S 证明。

2013 年，康威使用概率论证重新研究了这个问题，表明考拉兹猜想本身对于数学中常用的公理系统来说是不可证明的。这不是对考拉兹猜想的不可判定性的最终证明。但是，他提出的论证类型似乎强烈表明，每个人在尝试证明该猜想时都会遇到困难并非偶然。

所有数学家都会遇到他们无法解决的问题，康威也不例外。然而，他作为逻辑学家的技能可能提供了一些安慰，使他能够证明不可判定性并阐述论点，表明这个简单但棘手的问题将无限期地继续挑战数学家。

生命游戏中的新模式

生命游戏于 1970 年首次在马丁·加德纳的《大众科学》杂志的“数学游戏”专栏中介绍，至今仍在研究中，它提出的所有谜题尚未解决。无限二维矩形网格中的正方形单元格可能是活着的或死亡的。或者，单元格可能会从活着（黑色）变为死亡（白色），反之亦然，从一代到另一代。或者，单元格可能会保持稳定，具体取决于其八个最近邻单元格是死亡还是活着。

演化规则可以用 12 个字来表达：如果有三个活着的邻居则出生；如果有两个或三个活着的邻居则生存。初始状态下只有少量活细胞的一些模式会增长到无限大。理想情况下，活细胞的数量与 n² 成正比增加，其中 n 是世代数。网格稳定部分中活细胞的最佳密度为 1/2。哈佛大学的诺姆·埃尔基斯在 1997 年用 29 页证明了这一点。

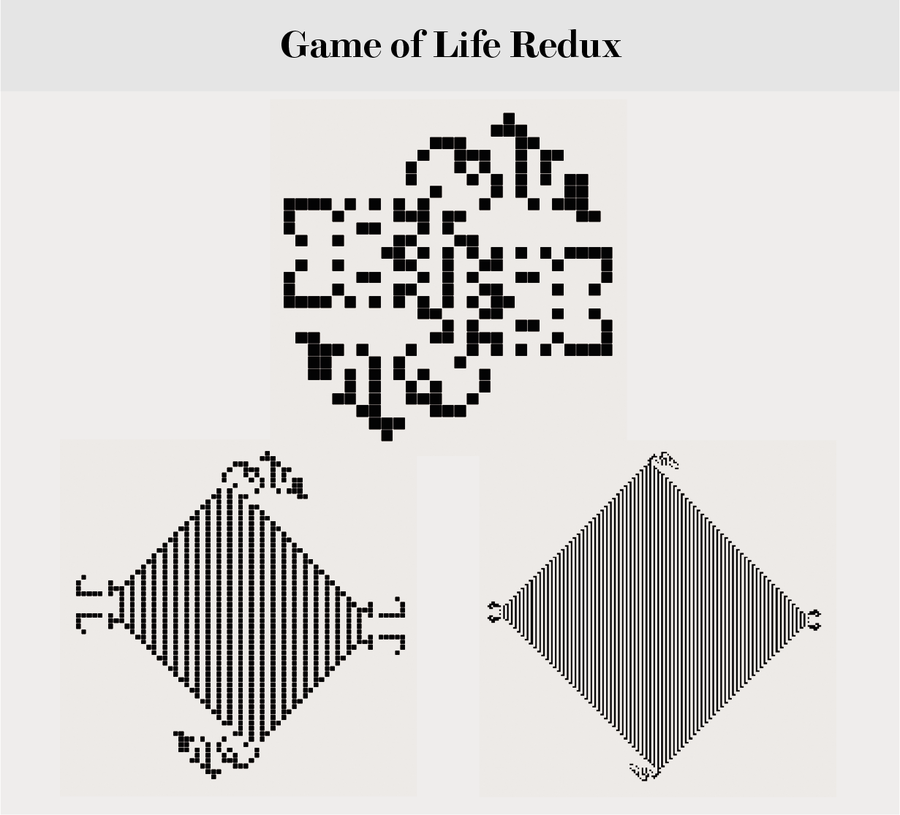
“生命游戏重制版”顶部显示的非凡模式是由计算机科学家马特乌什·纳希谢夫斯基于 2020 年 4 月发现的。它是已知的最小模式，一旦启动，就会呈二次方增长，以覆盖密度为 1/2 的稳定活细胞群体的网格。（因此，这种模式在速度和密度方面是最佳的。）配置以 183 个单元格的群体开始。我们绘制了第 0 代和另外两个不同比例的世代 [参见“生命游戏重制版”中的底部模式]。据信不可能做得比 183 个更好，但这尚未得到证明。还要注意，有些模式可以计算素数，甚至可以显示 π = 3.14159... 的十进制数字的图形图像，一个接一个。

本文最初发表在《Pour la Science》杂志上，经许可转载。