编者按:本文发表于1956年,非常受欢迎,启发了马丁·加德纳的传奇《大众科学》专栏《数学游戏》。在我们的特别数字期刊《乐趣与游戏》中阅读更多内容。
数学在很大程度上归功于游戏,反之亦然。有一个引人入胜的小练习,用纸条进行,近年来吸引了一些一流的头脑。它是一位在普林斯顿大学的英国数学系学生在闲暇时发现的。整件事源于一个微不足道的情况,即英国和美国的笔记本纸张尺寸不同。亚瑟·H·斯通,一位23岁的英国研究生,于1939年秋季获得奖学金来到普林斯顿,他发现自己必须从美国笔记本纸上修剪掉一英寸,才能将它们放入他的英国活页夹中。为了消遣,他开始以各种方式折叠修剪下来的纸条,他制作的一个图形结果特别有趣。他将纸条在三个地方斜向折叠,并将两端连接起来,使其成为一个六边形[见下图插图]。当他将两个相邻的三角形捏合在一起,并将六边形相对的顶点推向中心时,六边形会像含苞待放的花朵一样再次张开,并显示出一个全新的面。例如,如果原始六边形的顶面和底面被涂成不同的颜色,那么新出现的面将是空白的,而其中一个彩色面将消失!
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
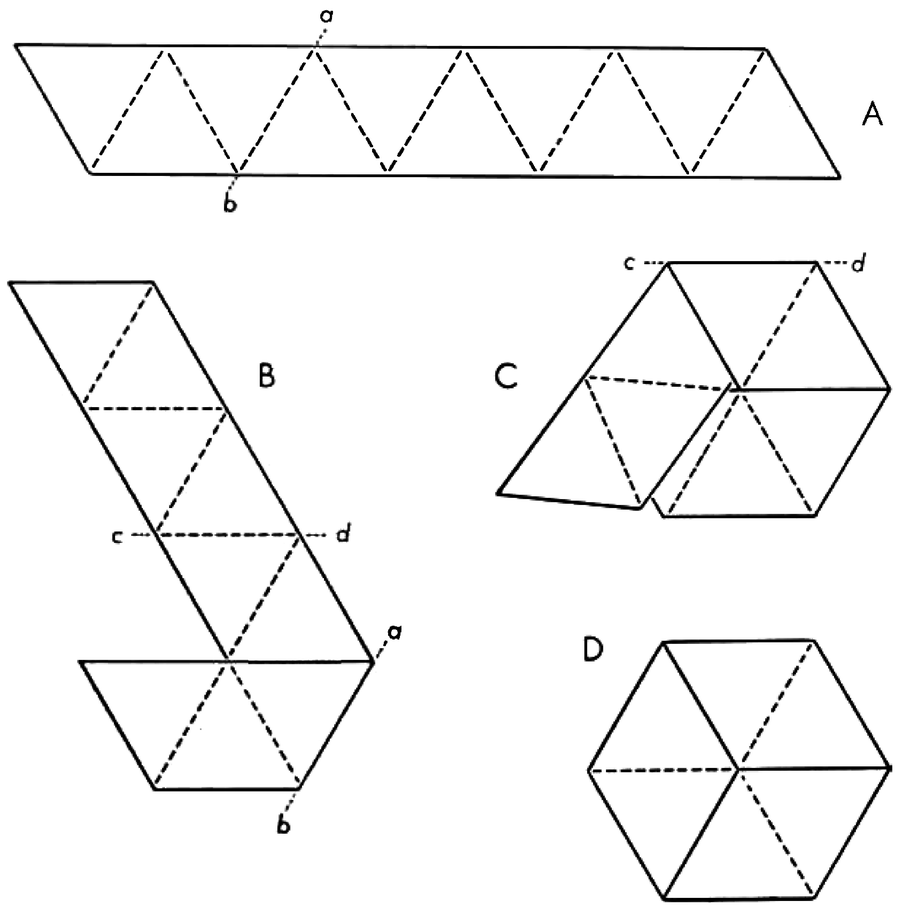
三六边柔韧环是由切割纸条制成的,使其可以标记为10个等边三角形(A)。纸条沿线ab向后折叠并翻转(B)。然后再次沿线cd向后折叠,并将倒数第二个三角形放在第一个三角形的顶部(C)。现在将最后一个三角形向后折叠并粘贴到第一个三角形的另一侧(D)。该图形可以如下图所示弯曲。它不是要被剪下来的。建议使用至少一英寸半宽的相当硬的纸张。
文治·田川
这个图形有三个面——比如,红色、绿色和空白。斯通进一步试验了更长的纸条,并且凭借相当的耐心和创造性的洞察力,他能够构建一个模型,该模型具有相同的六边形形状,但可以打开到六个不同的面,而不是只有三个。在这一点上,斯通发现这个游戏非常有趣,以至于他向研究生院的朋友展示了他的纸模型。“柔韧环”很快就在午餐和晚餐桌上大量涌现。组织了一个“柔韧环委员会”,以进一步探究柔韧环的奥秘。除了斯通之外,其他成员还有数学研究生布莱恩特·塔克曼;物理学研究生理查德·P·费曼;以及年轻的数学讲师约翰·W·图基。
这些模型被命名为六边柔韧环——“hexa”代表构成六边形面的六个三角形,“flexagon”代表结构的弯曲能力。斯通的第一个模型是三六边柔韧环(“tri”代表可以显示出来的三个不同面);他优雅的第二个结构是六六边柔韧环(代表它的六个面)。
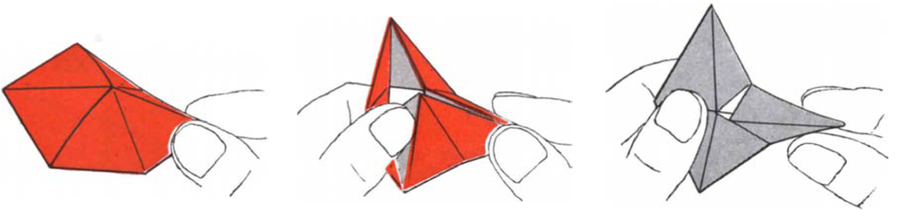
三六边柔韧环通过捏合其两个三角形来弯曲。可以用另一只手打开两个相对三角形的内边缘(中间)。如果图形无法打开,则捏合相邻的一对三角形。如果图形打开,则可以将其翻转过来,露出之前不可见的一侧。
文治·田川
要制作六六边柔韧环,您需要从一张纸条开始(加法机中使用的纸带非常适用),该纸条被分成19个三角形[见下图插图]。您在一侧的三角形上编号1、2和3,将第19个三角形留空,如图所示。在三角形的另一侧,根据所示方案编号为4、5和6。现在您折叠纸条,使相同的底面数字彼此相对——4对4,5对5,6对6,依此类推。由此产生的折叠纸条,如下图中的第二个图所示,然后在线ab和cd上向后折叠[插图中的第三个图],形成六边形[插图中的第四个图];最后,将空白三角形翻转到下方并粘贴到纸条另一侧的相应空白三角形上。所有这些用标记好的纸条进行比描述更容易执行。
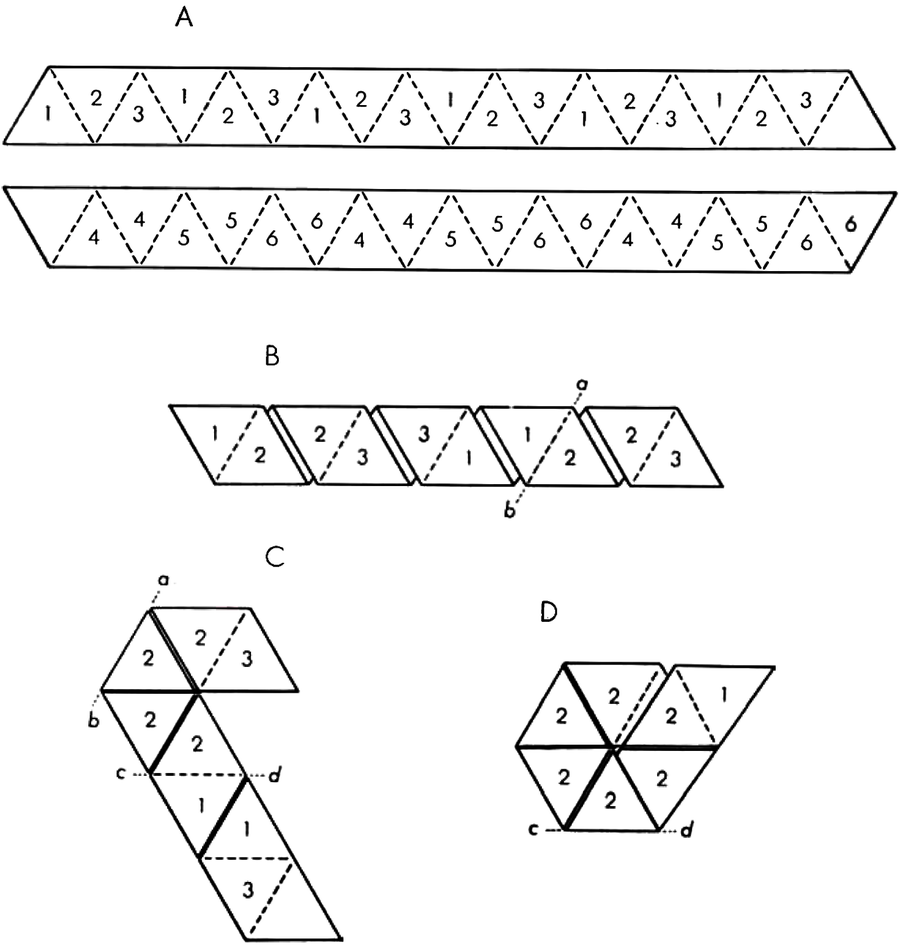
六六边柔韧环是由切割纸条制成的,使其可以标记为19个三角形(A)。一侧的三角形编号为1、2和3;另一侧的三角形编号为4、5和6。也可以使用类似的颜色或几何图形图案。然后如图所示折叠六边形。该图形可以弯曲以显示六个不同的面。
文治·田川
如果您正确地进行了折叠,则六边形的一个可见面上的三角形都编号为1,而另一面上的三角形都编号为2。您的六六边柔韧环现在可以弯曲了。您将两个相邻的三角形捏合在一起,沿着它们之间的线弯曲纸张,然后推入相对的顶点;然后图形可能会打开以显示面3或5。通过随机弯曲,您应该能够毫不费力地找到其他面。面4、5和6比1、2和3更难揭示。有时您可能会发现自己陷入一个令人恼火的循环中,该循环不断重复返回相同的三个面。
塔克曼很快发现,显示任何柔韧环的所有面的最简单方法是保持在同一顶点弯曲它,直到它拒绝打开,然后转移到相邻的顶点。此过程称为“塔克曼遍历”,将在12次弯曲的循环中显示六六边柔韧环的六个面,但1、2和3面出现的频率是4、5和6面的三倍。

“塔克曼遍历”在12次弯曲中显示了六六边柔韧环的所有六个面。在此,前图中柔韧环的数字已被相同模式的几何图形取代。面1、2和3出现的频率是面4、5和6的三倍。
文治·田川
委员会发现,通过加长三角形链,可以制作具有9、12、15个或更多面的柔韧环:塔克曼设法制作了一个可行的48面模型!他还发现,使用锯齿形纸条(即,边缘为锯齿状而不是直线的纸条),可以制作四六边柔韧环(四个面)或五六边柔韧环。有三种不同的六六边柔韧环——一种由直纸条折叠而成,一种由弯曲成六边形的链条折叠而成,还有一种由有点像三叶草的形状折叠而成。十六边柔韧环(10个面)有82种不同的变体,全部由奇特弯曲的纸条折叠而成。柔韧环可以形成任意所需的面数,但超过10个面后,每种物种的不同变体数量会以惊人的速度增加。顺便说一句,所有偶数面的柔韧环都是由具有两个不同面的纸条制成的,但具有奇数面的柔韧环只有一个面,就像莫比乌斯曲面一样。
图基和费曼在1940年制定了一个完整的柔韧环数学理论。它显示了除其他外,如何精确地构建任何所需尺寸或种类的柔韧环。该理论从未发表过,尽管此后其他数学家重新发现了其中的一部分。柔韧环研究者中包括塔克曼的父亲,杰出的物理学家路易斯·B·塔克曼,他以前在国家标准局工作。塔克曼高级工程师为该理论设计了一种简单而有效的图解符号。
珍珠港事件叫停了委员会的柔韧环计划,战争工作很快将四位创始成员分散到各地。斯通现在是英国曼彻斯特大学的数学讲师。费曼现在在加州理工学院,是一位著名的理论物理学家。图基是普林斯顿大学的数学教授,他对拓扑学和统计理论做出了杰出贡献,这为他赢得了世界范围的认可。塔克曼是普林斯顿高等研究院的著名数学家,他在该研究院的电子计算机项目上工作。
委员会希望有一天能共同撰写一两篇论文,这将是对柔韧环理论的权威阐述。在那之前,我们其他人可以自由地弯曲我们的柔韧环,看看我们自己能发现多少理论。
