所有篮球迷都知道手感火热:将球传给处于得分连胜的队友,因为她或他投进下一个球的机会比平时更高。这个备受推崇的原则在 1985 年被托马斯·吉洛维奇、罗伯特·瓦隆和阿莫斯·特沃斯基推翻。他们对费城 76 人队的投篮命中率数据、波士顿凯尔特人队的罚球数据以及康奈尔大学校队和少年队篮球运动员进行的 100 球/人受控实验的统计研究似乎证明,这种得分连胜并非不同寻常。尽管球迷认为他们的球员手感火热,但连胜可以用纯粹的运气来解释。
这个改变游戏规则的消息在职业体育界反响平平。当手感火热研究发布时,波士顿凯尔特人队总裁雷德·奥尔巴赫就特沃斯基发表了他的看法:“这家伙是谁?所以,他做了一项研究。我一点也不在乎。”
然而,学术界似乎对这一发现很着迷。1985 年的研究引发了大量的学术文献,而手感火热问题推动了对专业人士的直觉与冷冰冰的科学事实之间冲突的调查。在他的畅销书《撤销项目》中,迈克尔·刘易斯讲述了阿莫斯·特沃斯基和他的终身合作者、诺贝尔奖获得者丹尼尔·卡尼曼的故事。他们的研究促使了行为经济学的研究,并改变了我们对人类决策缺陷的理解。刘易斯写道:“特沃斯基清楚地知道人们是如何误解随机性的……人们有不可思议的能力在根本不存在的模式中看到意义。”
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
在他们的职业生涯早期,阿莫斯·特沃斯基和丹尼尔·卡尼曼考虑了人类根据少量观察得出结论的倾向,他们称之为“小数定律”。这是对大数定律的一种戏谑的暗示,大数定律提供了关于何时可以从大型数据集得出准确推论的指导。关于如何从小数据集得出推论没有通用的规则,而且可能很难注意到存在问题。
手感火热的基本统计公式
在统计实验中,有很多方法可以表示“手感火热”的概念。在本研究和原始研究中一样,手感火热是指在连续命中投篮的情况下,投篮命中的概率异常高。
这个公式忽略了比赛的一些细节。有些投篮比其他投篮更难,而且对方的防守动作可能会使表现出色的球员处于不利的位置。尽管如此,在尝试增加真实感之前,先看看这个简单实验的结果是很有趣的。
对于“异常高”这个术语,也有很多种定义方法。我们再次遵循原始的手感火热研究,该研究依赖于条件概率的差异:在连续命中投篮的情况下投篮命中的概率减去在同样长的连续不中投篮的情况下投篮命中的概率。如果观察到的差异相对于与相同长度和相同命中次数的随机字符串对应的典型差异较大,则该观察结果对应于手感火热。
原始手感火热研究中的“小数定律”错误及更正
2015 年,统计学家乔什·米勒和亚当·桑朱尔乔记录了原始手感火热研究中的一个错误。该错误与小数定律有关。为了理解这个错误,请考虑克莱·汤普森在 2016 年 12 月 23 日对阵底特律活塞队的比赛中的投篮记录。该记录用一串 1(命中)和 0(不中)表示
1110100110000011:
汤普森在这场比赛中出手 16 次,碰巧他正好投中了一半。我们可以看看我们关于这个字符串上手感火热的统计公式。首先,我们计算在之前两次命中的情况下命中的经验概率。有四次连续两次命中的情况,用字符串 11 表示。我们知道前三次 11 的情况之后发生了什么:汤普森第一次命中,第二次和第三次不中。但在第四次 11 的情况之后什么也没有发生,因为比赛在他可以再次投篮之前就结束了。我们将最后的 11 称为未实现的条件集,它使手感火热研究中使用的条件概率的估计复杂化。
也许我们能说的最好的是,在正在考虑的比赛中,我们观察到汤普森在连续两次命中后三分之一的时间得分。在另一个方向,鉴于汤普森连续两次不中,他五分之二的时间得分。第二个计算更直接,因为没有未实现的条件集。两个条件概率的差是 1/3 - 2/5 = -1/15。
这个差异 -1/15;异常高吗?也许对于这个一半命中一半不中的字符串,有一个自然的基准来衡量“异常”。根据数据,也许可以合理地假设在两次命中后投篮命中的概率与在两次不中后投篮命中的概率相同:50%。与此基准相比,条件概率的平均差为 0,这使得 -1/15 看起来并不异常高。这个基准与原始的手感火热研究一致。
然而——这就是小数定律发挥作用的地方——50-50 基准是错误的选择。如果我们处理的是无限字符串,那么这将是正确的,但比赛不会无限期地进行下去。在实践中,我们处理的是有限字符串。许多字符串都有未实现的条件集,有些字符串根本没有条件集,因此自然基准需要小样本调整。在长度为 16 的字符串中,一半是 1,一半是 0,在两次命中后投篮命中的概率小于在两次不中后投篮命中的概率:反转比延续更可能发生。这就是米勒和桑朱尔乔的观察结果,它与赌徒谬误一致,即认为命运的逆转是“应该”发生的。考虑到这种现象,条件概率的预期差值小于零。这为一项研究留下了可能性,该研究使用不正确的 50-50 零假设,在正确指定的零分布会导致拒绝的情况下,未能拒绝零假设。
原始研究中没有手感火热的结论是基于观察到的数据与错误的基准之间的统计上不显着的差异。当对康奈尔大学球员进行的 100 球/人受控实验应用所需的调整时,米勒和桑朱尔乔报告说,在几个案例中,没有手感火热的发现被推翻了。
寻找勇士队的手感火热
正如米勒和桑朱尔乔指出的那样,观察到的命中和不中字符串的排列检验会自动实现小样本校正 [2,第 3.1 节]。在该检验中,特定零和一字符串的属性与字符串条目的随机重排中的相同属性进行比较。这允许对属性的稀有性进行定量评估。
在这里,我们使用排列检验来确定库里、汤普森和杜兰特在哪些比赛中手感火热,根据原始研究中的公式。我们还逐节调查了勇士队的手感火热程度。
数据
对于库里、汤普森和杜兰特,我们编制了一个由 1 和 0 组成的字符串,表示他们在 2016-2017 赛季常规赛和季后赛中每场比赛的命中和不中情况。库里打了 96 场比赛,汤普森打了 95 场,杜兰特打了 77 场。我们还编制了勇士队逐节的命中和不中字符串,在整个赛季中,共得出 396 = 99 x 4 节。
实验设计和检验统计量
观察值 X 是库里、汤普森或杜兰特一场比赛的命中和不中字符串,或者是勇士队一节比赛的命中和不中字符串。该字符串包括投篮和罚球。我们使用排列检验来确定观察值是否显示出手感火热的证据。
对于观察到的字符串,我们计算了检验统计量 tk;给定 k 次先前命中的条件下命中的条件分数减去给定 k 次先前不中的条件下命中的条件分数,其中 k 等于 1、2 或 3。然后,我们对表示投篮模式的 0 和 1 字符串进行 10,000 次排列,并计算每个排列的 tk。
从数学上讲,长度为 L 的字符串 X 上的检验统计量 tk 定义如下
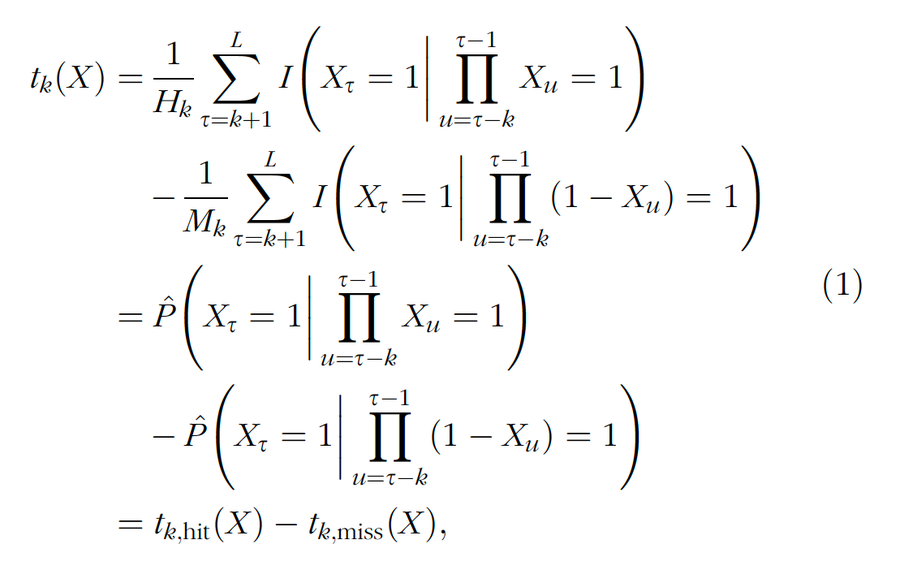
其中 Hk 和 Mk 是由投篮紧随其后的 k 次命中和 k 次不中的子字符串的数量,Xτ 是 X 的第 τ 个条目,而 P̂ 是经验概率。值 k 是条件集的深度。
超过观察到的检验统计量的排列检验统计量的分数是其 p 值。在实践中,许多排列字符串上的检验统计量的值与观察到的投篮模式上的检验统计量的值相同。因此,在如何定义 p 值方面存在一定的自由度。从数学上讲,这种自由度对应于以下两者之间的选择
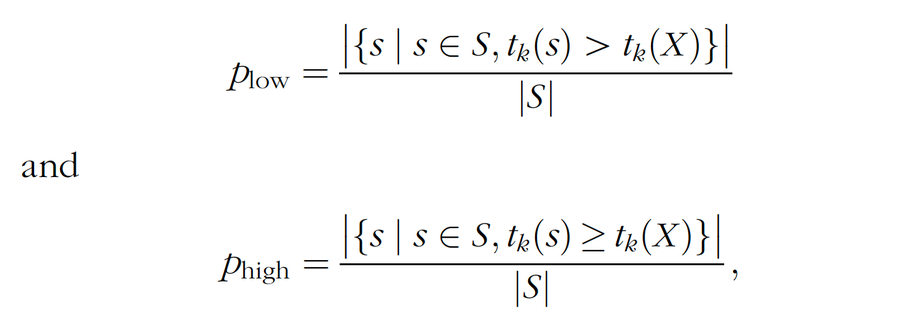
其中 S 是排列字符串的集合。我们使用 Plow;这使得尽可能容易地拒绝“没有手感火热”的零假设。较小的 p 值对应于手感火热的更强证据。
结果
描述投篮次数和命中频率的统计数据显示在表 1 中。
下面呈现的结果主要关于 t2;它没有显示出手感火热的证据。t3 的结果在质量上相似,尽管 t1 中有手感火热的迹象:在 96 场比赛中,斯蒂芬·库里的投篮字符串在条件集深度为 1 的情况下,在 5% 的水平上显着。同样,勇士队作为一个团队在使用 t1 的 396 节比赛中,有 35 节比赛显示出手感火热的迹象:但是,我们认为这些结果构成了支持手感火热的微弱证据,因为在不太宽松的测试条件下,明显的效应消失了。也就是说,当我们使用更传统的 p 值计算方法 Phigh(如上一节所述)时,库里的显着比赛场次降至 96 场中的 7 场,勇士队的显着节数降至 396 节中的 26 节。此外,当我们删除罚球数据时(球员的罚球命中率往往高于正常比赛期间),库里的表现仅在 5 场比赛中具有统计学意义,而勇士队仅在 21 节比赛中具有统计学意义。有关更多详细信息,请参见附录。
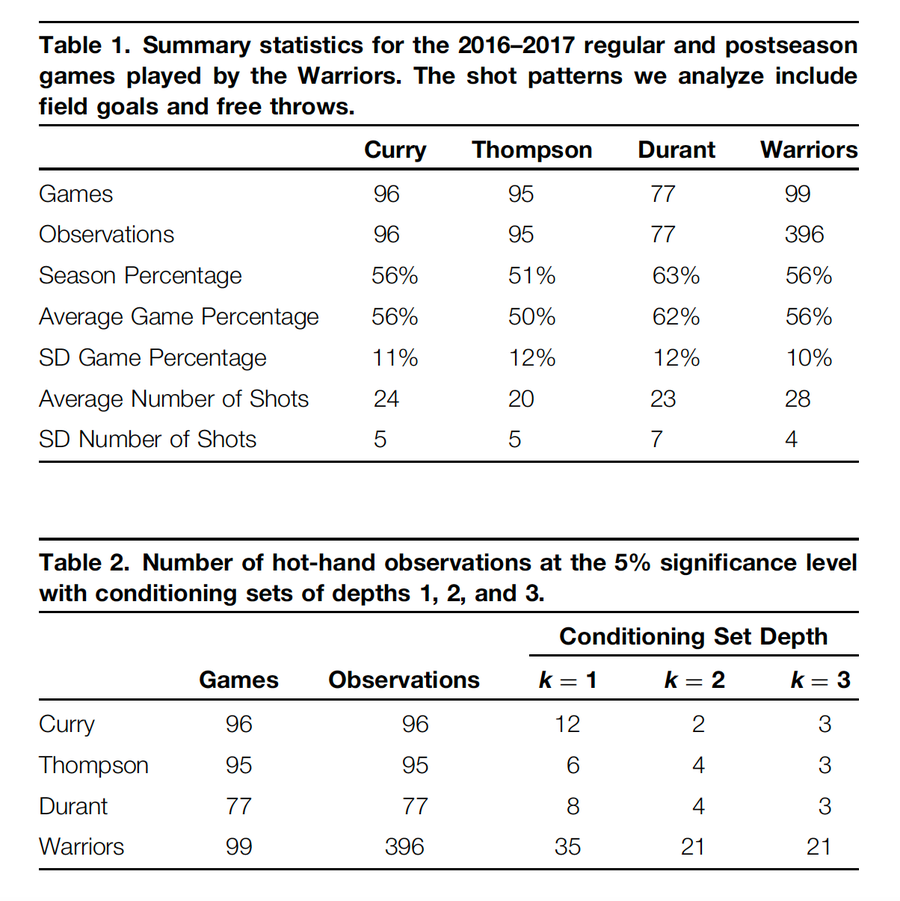
表 2 显示了在 2016-2017 赛季库里、汤普森和杜兰特进行的比赛以及勇士队进行的节数中,深度为 1、2 和 3 的条件集在 5% 水平上显着的观察次数。在 5% 水平上显着的观察结果很少。
除了原始手感火热研究中的 tk 统计量外,我们还考虑了许多其他可能指示手感火热的统计量。我们只查看了 tk 的左和项;tk,hit:在这种情况下,我们测试了手感火热的更简单的定义:如果球员在连续成功投篮后投篮命中的机会更高,则该球员手感火热。“机会更高”的概念在此处的定义方式与上述测试中相同。
对于我们的两个检验统计量,我们还考虑了两个额外的非参数检验。首先,我们没有排列给定比赛的投篮字符串,而是通过模拟 10,000 个新的二元字符串来估计检验统计量的分布,方法是模拟 n 次伯努利 (p) 试验,其中 p 是该球员在该比赛中的投篮命中率,n 是该球员的投篮次数。在第二个测试中,我们再次模拟了 n 次伯努利试验;但是,我们让 p 等于被测试比赛开始时球员的赛季投篮命中率。这些替代公式得出了相同的结论:很少或没有手感火热的证据。
一个例子
2016 年 12 月 5 日,汤普森对阵印第安纳步行者队得到 60 分。他 44 次投篮命中 31 次,他在该场比赛中的记录如下所示
X60: 11011110010111111001110111101110111101010101
这是否表明手感火热?有 19 次字符串 11 的实例,其中 12 次后面跟着命中。有两次字符串 00 的实例,它们后面都跟着命中。因此 t2 = 12/19 - 1 = -7/19。
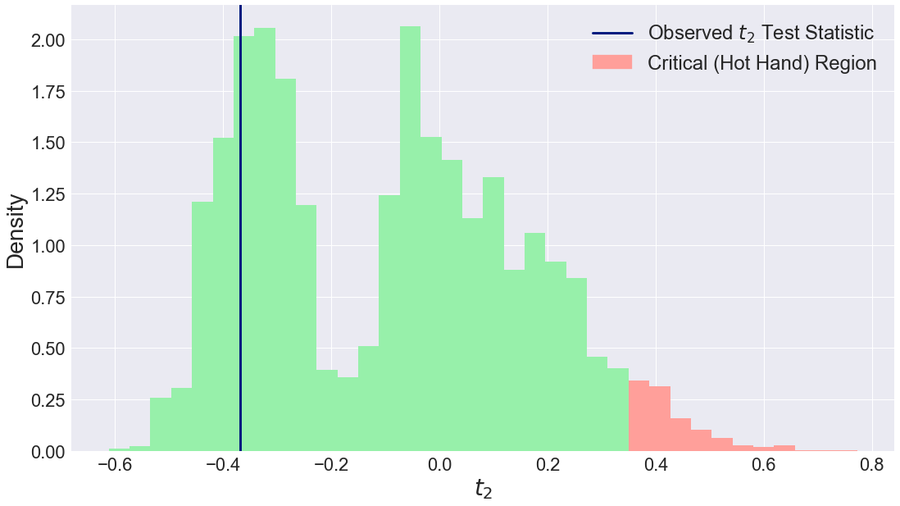
图 1. 汤普森 2016 年 12 月 5 日对阵印第安纳步行者队的 60 分比赛的 t2 统计量。绿色区域代表零假设,对应于观察到的字符串的 10,000 次排列的 t2 值的直方图。蓝线标记观察到的字符串的 t2 值,红色临界区域对应于 t2 值最高的 5%:手感火热。图片来源:阿隆·达克斯
图 1 显示了基于汤普森 X60 字符串的 10,000 次排列的 t2 统计量的直方图。绿色区域代表零分布,对应于观察到的字符串的 10,000 次排列的 t2 值的直方图。在附录中,我们探讨了零假设的双峰性及其形状的其他不规则性。蓝线标记观察到的字符串的 t2 值,红色临界区域对应于 t2 值最高的 5%:手感火热。
这个观察结果因其长度而非常特殊,而且因其命中百分比 31/44 ≈ 70% 而非常特殊:但条件概率的差异 -7/19;的 p 值为 0.84,这根本不特殊。
最终观察
尽管我们像统计学家一样检查了“水花兄弟”斯蒂芬·库里和克莱·汤普森以及 2016-2017 赛季常规赛的射击记录以及 2017 年总决赛 MVP 凯文·杜兰特的射击记录,但我们希望指出,观看这些球员在球场上的比赛是一种神奇的体验。当他们进入状态时,他们似乎就是手感火热的化身。然而,我们的统计研究讲述了一个不同的故事。它表明,在 2016-2017 赛季的大部分常规赛比赛中,他们都不是连胜射手。因此,在调整了小样本效应后,我们的结论与最初的结论相似,后者没有考虑到小样本效应。
当然,这并不是故事的结局。手感火热长期以来一直让体育专业人士和研究人员着迷,我们对于思考这个问题的正确方法尚未达成共识。然而,每项实证手感火热研究都将依赖于有限的数据集,因此小样本效应势必会在对结果的任何正确解释中发挥作用。
阿莫斯·特沃斯基于 1996 年去世,享年 59 岁,距离他本应与丹尼尔·卡尼曼分享的诺贝尔奖颁发还有五年,距离发现他的手感火热研究中的错误还有近二十年。如果他今天与我们同在,这位了不起的研究人员和狂热的篮球迷无疑会对他的错误的纠正感到高兴,并且他肯定会观看引人入胜的金州勇士队的比赛。
附录:解构 t2 的零假设
在本附录中,我们将更仔细地研究图 1 中描绘的汤普森对阵印第安纳步行者队的 60 分比赛的零假设。公式 (1) 将 t2 表示为概率差
tk = tk,hit - tk,miss。
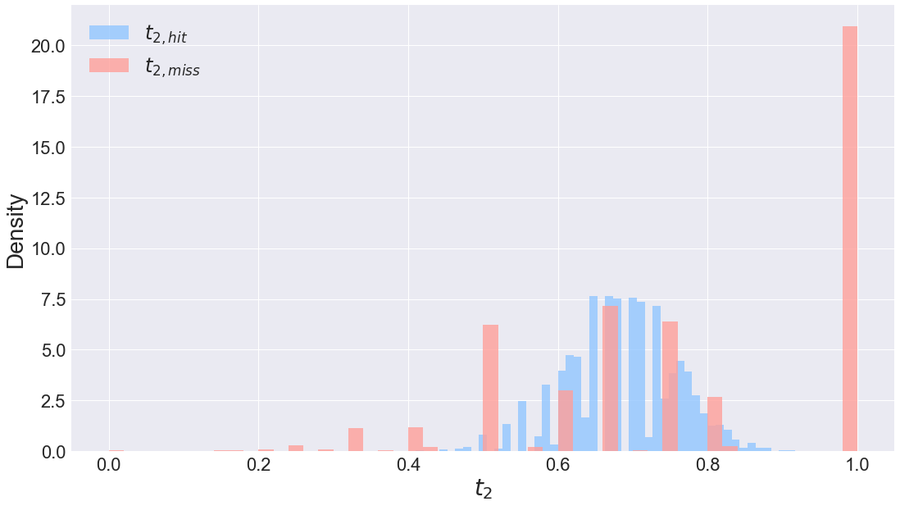
图 2. 汤普森 2016 年 12 月 5 日对阵印第安纳步行者队的 60 分比赛的 t2,hit 和 t2,miss 直方图。图片来源:阿隆·达克斯
在图 2 中,我们显示了 tk,hit 和 tk,miss 的直方图。这些直方图的形状完全由字符串的长度 44 和命中百分比 31/44 ≈ 70% 决定:t2,miss 在 1 处的峰值出现是因为不中投篮相对罕见:在许多长度为 44 且命中次数为 31 的字符串中,所有连续的后面跟着任何东西的不中对都跟着命中。
对于较长的字符串和 50% 左右的命中概率,t2 及其分量的分布往往是单峰且对称的。但是对于相对较小的字符串,例如,顶级职业篮球运动员在一场比赛中的投篮次数,表示 t2 及其分量的零假设的直方图可能是不规则的。因此,本文中使用的类型的有限样本方法可能优于渐近结果。
仅限投篮
本文分析的字符串包括投篮和罚球。然而,当我们分析投篮字符串时,我们的结论是相同的。
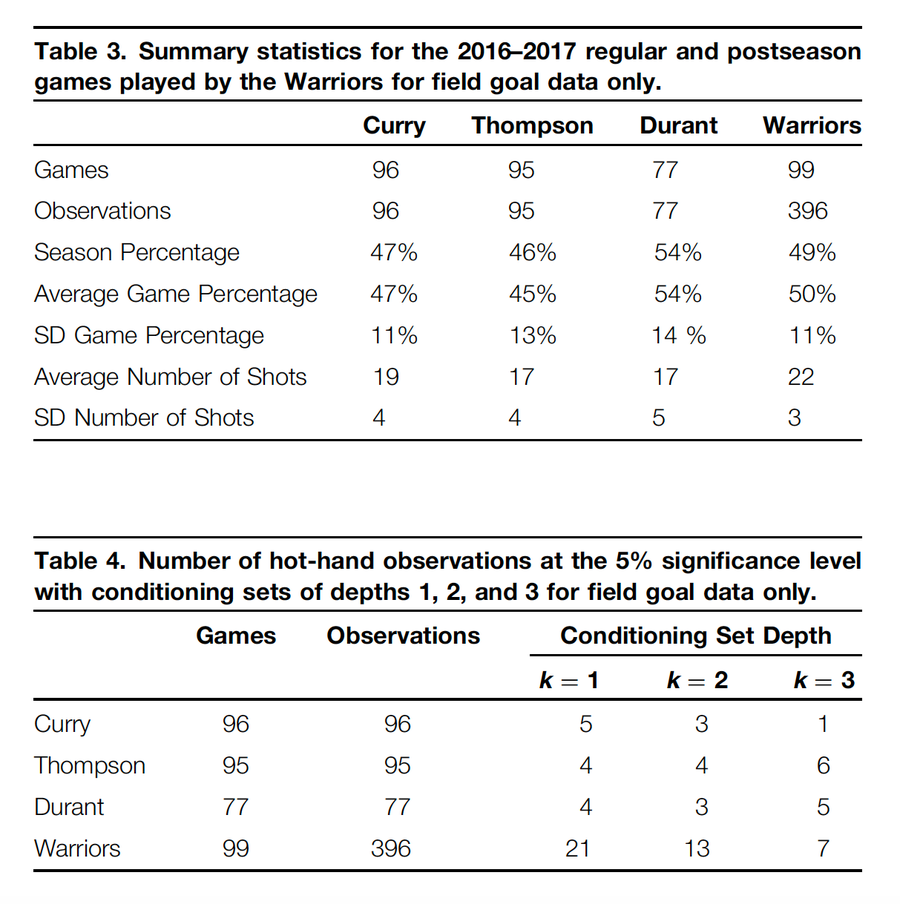
描述尝试投篮和命中频率的统计数据显示在表 3 中。表 4 显示了在 2016-2017 赛季库里、汤普森和杜兰特进行的比赛以及勇士队进行的节数中,深度为 1、2 和 3 的条件集在 5% 水平上显着的观察次数。在 5% 水平上显着的观察结果很少。
经《数学情报家》许可转载。
