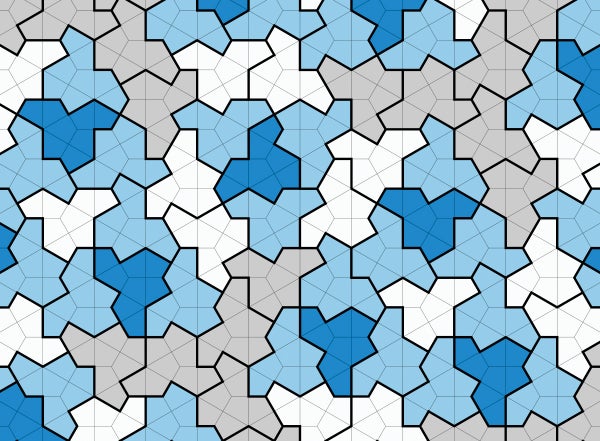
来自英国约克郡的数学爱好者大卫·史密斯发现了一种 13 边形,这个形状几十年来一直让数学家们捉摸不透。这种崎岖不平、类似帽子的形状被称为“爱因斯坦”,源自德语中的“一块石头”。如果您使用爱因斯坦形状的瓷砖来铺设浴室地板——或任何平面,即使是无限大的平面——它们将完美地拼合在一起,但永远不会形成重复的图案。几十年来,数学家们一直在寻找像这样的瓷砖形状,它们只能形成非重复排列,称为非周期性平铺。他们从多组不同的瓷砖开始:第一组于 1964 年被发现,需要 20,426 块不同的瓷砖,后来简化为 103 块。到 1974 年,数学家罗杰·彭罗斯发现了两种瓷砖形状,当它们组合成马赛克时,永远不会形成重复的图案。
但是,是否有可能仅用一种形状的瓷砖——假设的爱因斯坦瓷砖——形成非周期性平铺?多丽丝·沙茨施耐德是一位退休数学家,隶属于莫拉维亚大学,在镶嵌方面拥有专业知识,她一直对真正爱因斯坦瓷砖被发现的可能性持怀疑态度。“这就是为什么不仅发现了它,而且它还是如此简单的瓷砖,这令人如此震惊,”她说。“对我来说,这是一个完全的异常现象。”史密斯于 2022 年 11 月发现的瓷砖,当时他正在使用名为 PolyForm Puzzle Solver 的软件试验不同的形状,其优雅性令人震惊。它由直角风筝形组成,与许多数学家预测的粗糙、复杂的形状截然不同。
史密斯给安大略省滑铁卢大学的计算机科学家克雷格·卡普兰发送了电子邮件,卡普兰认识到了这种形状的潜力。尽管它创建的马赛克似乎没有重复的图案,但两人需要从数学上证明它永远不会——即使马赛克是无限大的。他们请来了软件开发人员约瑟夫·塞缪尔·迈尔斯和阿肯色大学数学家查伊姆·古德曼-施特劳斯,他们过去都曾从事平铺和组合数学方面的工作。
支持科学新闻报道
如果您喜欢这篇文章,请考虑支持我们屡获殊荣的新闻报道,方式是 订阅。通过购买订阅,您正在帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。
研究人员使用了两种方法来证明他们手中拥有真正的爱因斯坦瓷砖。首先,他们表明,当帽子状瓷砖排列在一起时,会形成四种特定的形状。添加更多瓷砖会形成这些相同形状的更大版本,或“超瓷砖”;添加的瓷砖越多,超瓷砖就越大。数学家已经证明,这种分层结构意味着平铺无法分割成重复的部分,因此必须是非周期性的。对于第二个证明,该团队发明了一种新方法,可以将帽子平铺与更著名的称为多边形钻石的形状的非周期性平铺进行比较。在这个过程中,该团队还表明,人们可以通过调整某些边的长度来制作无限数量的类似爱因斯坦瓷砖。
即使有了这些证明,数学家们还没有制定出更广泛的理论来解释为什么这种简单的帽子形状如此特别。“这仍然非常神秘,”新泽西州普林斯顿高级研究所的数学家雷切尔·格林菲尔德说。可能还有更多类别的爱因斯坦瓷砖有待发现,但几何帽子并没有透露任何线索,隶属于史密斯学院的退休数学家马乔里·塞内沙尔说:“这些东西是你偶然发现的。”
编者注:此故事的早期版本曾在网上以标题 “新发现的数学“爱因斯坦”形状创造了一种永不重复的图案”发表。