关键概念
圆
圆周长
直径
数学公式
圆周率
导言
数学家们对数学关系的发现感到兴奋。他们用数字、公式和方程式来看待周围的世界。数学也很有趣且实用。当计算您需要存多久的零用钱才能买一个新游戏时,它会派上用场。您可以使用数学来将食谱加倍或三倍,或者计算您最晚可以几点离开家,并且仍然可以准时到达学校。
您还可以使用它来预测事物的大小——在纸上或在现实世界中。在这个科学活动中,您将检查圆形物体,看看您能发现关于它们大小的哪些关系。您将探索圆的圆周长是否以某种特定的方式与其直径相关。当您探索这种关系时,您可能会对结果的有用性感到惊讶;也许它会激励您存钱买一辆更大的自行车!
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您正在帮助确保有关塑造我们今天世界的发现和想法的具有影响力的故事的未来。
背景
您知道人们研究数学已经有数千年了吗?我们今天使用的许多数学术语都源于希腊语和拉丁语,揭示了一些研究这些问题的古代学者的起源。例如,单词“circumference”(圆周长)来自拉丁语单词 circum(意思是“周围”)和 ferre(意思是“携带”)。它可以指圆的边界线,也可以指该线的长度。单词“diameter”(直径)源于希腊语单词 dia(“横穿”)和 metron(“测量”)。它指的是一条直线,该直线从圆周上的一个点开始,穿过圆心,并在圆的另一侧结束。它也可以指这条线的长度。数学家已经证明,直径也是穿过圆的最长距离。
术语够多了!是时候开始探索了。
材料
至少四个不同大小的圆形物体(例如,您可以使用大硬币、圆形容器盖、大型容器盖和自行车轮。)
一大卷细绳或丝带,您可以将其剪成小块
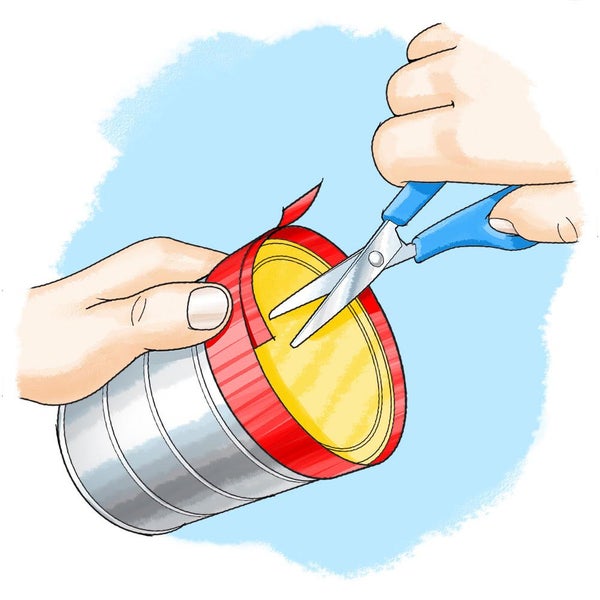
剪刀(应由成人帮助您使用。)
胶带,例如美纹纸胶带(可选)
准备
将您的所有物品集中在一个区域,以便于取用。
从一个中等大小的圆开始您的探索,例如酸奶容器盖。在接下来的几个步骤中,您将剪下几段细绳(或丝带),其长度分别为该圆的圆周长和直径。一旦您准备好这些线段,您就可以开始探索它们是否以某种特定的方式相关。您将对不同大小的圆重复此过程,以期发现您所有示例的直径和圆周长以相同的方式相互关联。
步骤
要创建一段长度等于第一个圆形物体的圆周长(圆的边界线)的细绳,请用拇指将一段细绳的一端按在圆形物体边缘上的一个点上。
将细绳绕物体正好一圈,并在缠绕的细绳与其起点相遇的地方剪断细绳。为了使操作更轻松一些,您可以暂时用胶带将细绳的开头粘在圆形物体上,然后缠绕细绳并沿着胶带剪断。您能看到您的细绳的长度正好是您的圆形物体的圆周长吗?
要测量直径,您需要一条直线的长度,该直线从圆周上的一个点开始,穿过圆心,并在其另一侧结束。因为不容易找到圆心,所以您将使用关于圆的数学事实,该事实指出直径也是穿过圆的最长距离。要创建一段具有穿过圆的最长长度的细绳,请用拇指将一段新的细绳(或丝带)的一端按在中等大小的圆形物体边缘上的一个点上。
将这段细绳拉直,横跨圆到圆周上的另一点。现在沿着圆周移动第二个点——向左和向右。这样做直到找到可能的最长的直线跨度细绳。当您将细绳的末端从该点移开时,跨度细绳又会变短。在细绳最长的地方剪断,以获得该圆的直径的测量值。您是否观察到您的跨度细绳穿过了圆心?
现在您拥有开始探索所需的一切。哪个距离更长——直径还是圆周长?是长很多还是长一点?
如果您将较长的细绳对折,它是否适合另一段细绳的长度?如果是这样,则意味着较长的细绳是较短的细绳的两倍长。如果您对折较长的细绳后没有找到合适的长度,那么如果您将其折叠成三份、四份或五份呢?您得到的是精确的还是近似的拟合?您将如何用“两倍长”或“三倍长”之类的词语来翻译您的发现?
用不同大小的圆形物体再次尝试该活动。您是否期望圆周长和直径长度之间的相同关系对于不同大小的圆也有效?
重复圆周长和直径的查找,直到您探索了一个微小、中等、大和非常大的圆。您能找到一个对所有测试的圆都有效的关系吗?它是精确的关系还是近似的关系?如果您找到了关系,您认为您有足够的数据来得出您的关系对所有圆都有效的结论吗?
额外内容:在房子周围寻找一些圆形物体,并估计这些物体的直径和圆周长的长度。对您来说,哪个更容易估计,直径还是圆周长?哪个更容易用尺子测量?
额外内容:如果您找到了圆周长和直径之间的近似关系,您如何使其更精确?提示:您可以使用尺子测量您的细绳的长度并进行一些数学运算。(例如,尝试将圆周长除以其对应的直径;对每个圆再次尝试。每次您是否得到相似的数字——无论圆的大小是否相同?)
额外内容:该原理的一个实际应用是计算不同尺寸的车轮行驶的距离。为了探索地面行驶距离和车轮尺寸之间的关系,用胶带在车轮(例如自行车轮)的圆周上标记一个点。将该点放在地面上,并在地面上用胶带或粉笔标记该位置。沿直线滚动车轮,直到圆周上的同一点再次接触地面。在地面上用胶带或粉笔标记该位置。现在将地面上两个标记位置之间的距离与车轮的直径和圆周长的长度进行比较。您能找到关系吗?对于较大或较小的车轮行驶相同距离可能需要的旋转次数,这意味着什么?
额外内容:既然您知道了直径与圆周长的关系——甚至可能知道了行驶距离——您能看到这种关系可以在哪些实际方面有用吗?
[break]
观察和结果
如果一切顺利,您应该已经发现,对于每个圆,无论圆的大小如何,圆周长都比直径略大三倍。
如果您能够更精确地工作,您可能会发现它不是正好三倍,而是直径的三又七分之一。即使这样也不精确。
数学家发现,圆的圆周长与直径之比是一个常数,这意味着对于所有圆,无论圆的大小如何,该比率都相同。然而,他们也发现,这个比率是一个永远无法精确确定的数字。自19世纪中期以来,这个比率一直用希腊字母 π(pi)表示,这是一个非常有趣的数字。它不仅出现在几何学中,也出现在其他数学领域,例如概率论。它也出现在自然界中,例如在波浪的描述中——从可见的水波纹到不可见的光波和声波。
更多探索 史前微积分:发现圆周率,来自Better Explained
用数学描述自然,来自NOVA 在圆周率日谈论圆周率和馅饼,来自Science Buddies
此活动由Science Buddies合作推出