数千年来,人们一直在玩魔方——由不同的数字组成的阵列,其行、列和对角线的总和都相同。*一个简单的 3x3 阵列,每种方式加起来都等于 15,出现在中国传说洛书的乌龟背上,该传说可以追溯到公元前 650 年。中东和印度的中世纪数学家研究了各种尺寸的魔方,阿尔布雷希特·丢勒在他 1514 年创作的著名版画《忧郁 I》中加入了一个 4x4 的魔方。今天,业余和专业数学家继续设计新的魔方,甚至增加额外的维度来设想 3D 魔方和 4D 魔方体。
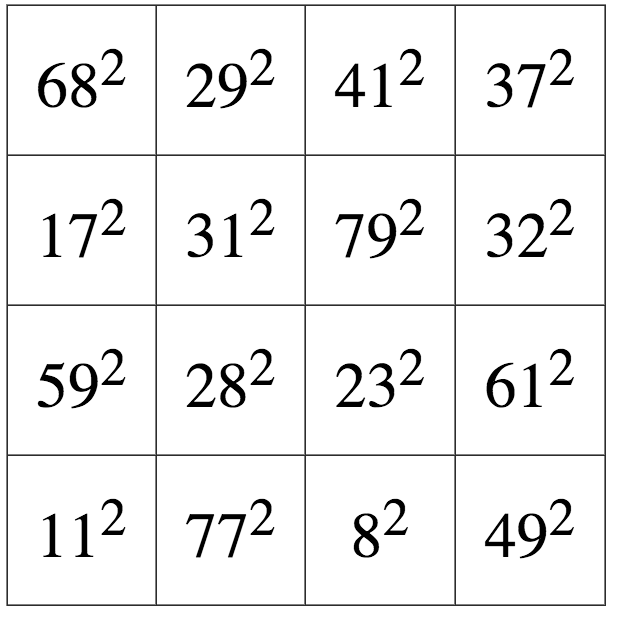
18 世纪的数学家莱昂哈德·欧拉对另一种奇异的魔方感到困惑,这种魔方完全由平方数构成。1770 年,他介绍了第一个 4x4 平方数魔方的例子(如下),以及生成其他魔方的公式。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。
现在已知许多 4x4 平方数魔方,大约 10 年前,克里斯蒂安·博耶报告了 5x5、6x6 和 7x7 平方数魔方的首批示例。然而,迄今为止,没有人发现 3x3 平方数魔方,也没有人证明这是不可能的。
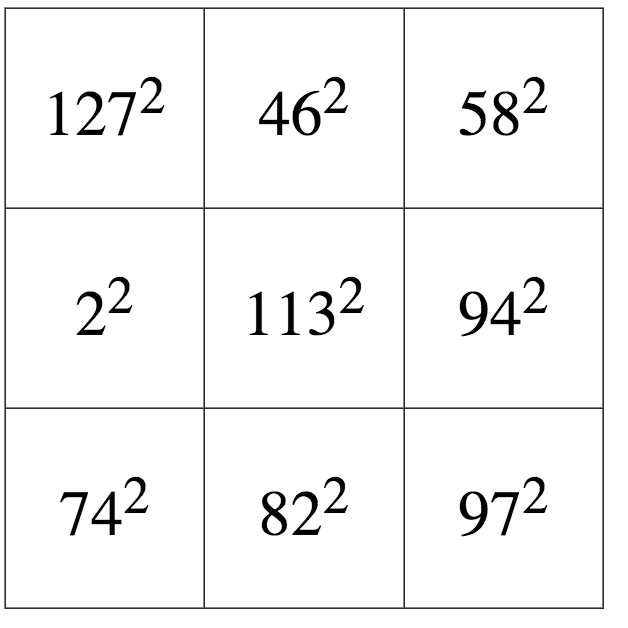
1996 年,为《大众科学》撰写“数学游戏”专栏约 25 年的马丁·加德纳向任何能够设计出解决方案的人提供了 100 美元的奖金。一年后,魔方专家李·萨洛斯描述了一个差一点成功的例子(见下文),只有一个对角线的总和不同(从左上到右下得到 38,307,而不是所有其他方向的总和 21,609)。
到目前为止,这是任何人所能达到的最接近的程度。您会成为第一个解决这两个问题的人吗?在下面发布您自己设计的解决方案和魔方。如果收到足够有趣的提交内容,其中一些将会在未来的博客文章中在 www.ScientificAmerican.com 上展示。*澄清(2014 年 10 月 20 日):此句子在发布后经过编辑。原文没有明确指出每个魔方中的数字彼此不同。
您需要启用 JavaScript 才能使用小部件。