谁会想到上帝会成为一篇关于数学文章的合适主题?别担心,接下来的讨论仍然牢牢扎根于可理解的科学框架内。但是,上帝是否可以用数学证明这个问题非常有趣。事实上,几个世纪以来,一些数学家不断尝试证明神的存在。他们包括布莱斯·帕斯卡和勒内·笛卡尔(17世纪)、戈特弗里德·威廉·莱布尼茨(18世纪)以及库尔特·哥德尔(20世纪),后者关于这个主题的著作最近在1987年才出版。最令人惊奇的是:在2013年首次发布的预印本研究中,一位算法证明向导检查了哥德尔的逻辑推理链——并发现它无疑是正确的。现在数学终于反驳了所有无神论者的主张吗?
正如您可能已经怀疑的那样,并没有。哥德尔确实能够证明,某种他定义为神圣的事物的存在,必然是从某些假设中推导出来的。但是,这些假设是否合理值得怀疑。例如,如果我假设所有的猫都是三色的,并且知道三色猫几乎总是雌性的,那么我可以得出结论:几乎所有的猫都是雌性的。即使逻辑推理是正确的,但这当然不成立。因为所有猫都是三色的这个假设是错误的。如果一个人对我们环境中可观察到的事物(例如猫)做出陈述,可以通过科学调查来验证它们。但如果是关于神圣存在的证明,事情就变得有点复杂了。
莱布尼茨、笛卡尔和哥德尔都依赖于上帝的本体论证明,他们通过逻辑推理从神圣存在的可能性中推导出其存在,而帕斯卡(1623-1662)则选择了略有不同的方法:他从今天可能被认为是博弈论的角度分析了这个问题,并发展了所谓的帕斯卡赌注。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
为了做到这一点,他考虑了两种可能性。第一,上帝存在。第二,上帝不存在。然后他考察了死后相信或不相信上帝的后果。如果存在神圣的存在,并且一个人相信它,那么他最终会进入天堂;否则就会下地狱。另一方面,如果没有上帝,那么什么也不会发生——无论你是否信教。帕斯卡认为,最好的策略是相信上帝。最好的情况是,你最终会进入天堂;最坏的情况是,什么也不会发生。另一方面,如果你不相信,那么在最坏的情况下,你可能会下地狱。
帕斯卡的思想是可以理解的——但它们指的是宗教著作中的场景,并不代表对至上存在者的存在证明。它们只是说,一个人应该基于机会主义加入信仰。
处理存在本质的本体论方法更具说服力,即使它们很可能不会改变无神论者的想法。神学家和哲学家坎特伯雷的安瑟尔姆(1033-1109)在上个千年初提出了他的想法。他将上帝描述为无法想象出比之更伟大的存在。但是,如果上帝不存在,那么人们可以想象出更伟大的事物:即,一个无法想象出比之更伟大的存在。但与上帝一样,这个存在也存在,并展现出终极伟大的属性。这当然是荒谬的:没有什么可以比一个人可以想象的最伟大的事物更伟大的。因此,上帝不存在的假设一定是错误的。
这个想法经过了几个世纪才被重新审视——由笛卡尔(1596-1650
)完成。据推测,他不了解安瑟尔姆的著作,但他为完美的神圣存在提供了几乎相同的论证。莱布尼茨(1646-1716)在几十年后继续这项工作,并发现了其中的缺陷:他认为,笛卡尔没有证明从三角形到上帝的某些实体的“完美属性”是相容的。莱布尼茨继续论证说,完美性无法得到适当的考察。因此,永远无法反驳完美属性在一个存在中结合的可能性。因此,神圣存在的可能性一定是真实的。因此,基于安瑟尔姆和笛卡尔的论证,必然得出上帝存在的结论。
然而,从数学的角度来看,这些思想实验只有通过哥德尔的努力才真正变得严肃起来。这并不太令人惊讶:这位科学家在25岁时就通过表明数学总是包含无法证明的真命题,从而颠覆了该学科。在这样做时,他使用了逻辑。同样的逻辑也使他能够证明上帝的存在。看看这12个步骤,它们由一组公理(Ax)、定理(Th)和定义(Df)组成。
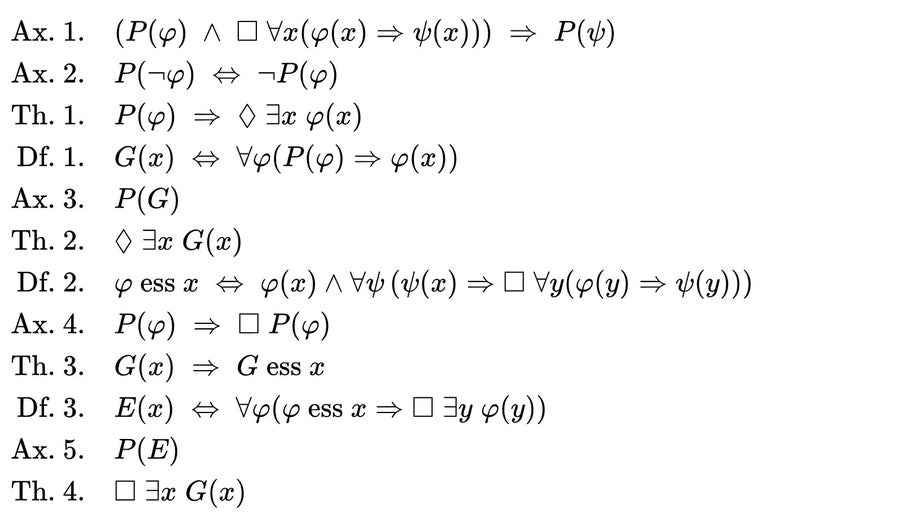
库尔特·哥德尔的形式证明。 来源:Spektrum der Wissenschaft(局部)
乍一看,它们似乎很神秘,但人们可以逐步了解它们,从而理解哥德尔的思维。他从一个公理开始——换句话说,一个假设:如果 φ 具有属性 P,并且从 φ 总是推出 ψ,那么 ψ 也具有属性 P。为简单起见,我们可以假设 P 代表“正面的”。例如:如果一种水果是美味的(一种正面属性),那么吃它也是有趣的。因此,吃它的乐趣也是一种正面属性。
第二个公理进一步为 P 设定了一个框架。如果某事物的反面是正面的,那么“某事物”一定是负面的。因此,哥德尔将世界划分为黑白两色:要么是好的,要么是坏的。例如,如果健康是好的,那么疾病必然是坏的。
有了这两个前提,哥德尔可以推导出他的第一个定理:如果 φ 是一个正面属性,那么存在一个具有属性 φ 的 x 的可能性。也就是说,正面事物有可能存在。
现在,这位数学家第一次转向对神圣存在的定义:x 是神圣的,如果它拥有所有正面属性 φ。第二个公理确保以这种方式定义的上帝不可能具有负面特征(否则就会产生矛盾)。
第三个公理指出,神性是一种正面特征。这一点实际上是无可辩驳的,因为神性结合了所有正面特征。
第二个定理现在变得更加具体:通过结合第三个公理(神性是正面的)和第一个定理(存在某种正面事物存在的可能性),一个存在物 x 可能是神圣的。
哥德尔现在的目标是在接下来的步骤中证明,在已经制定的框架内,上帝必然存在。为此,他在第二个定义中引入了对象 x 的“本质” φ,这是一种决定所有其他特征的特征属性。一个说明性的例子是“小狗般的”,如果某事物具有这种属性,那么它必然是可爱的、毛茸茸的和笨拙的。
第四个公理乍一看似乎不太令人兴奋。它只是简单地声明,如果某事物是正面的,那么它永远是正面的——无论时间、情况或地点如何。例如,小狗般的和味道好总是正面的,无论是在白天还是晚上,在德国海德堡还是在阿根廷布宜诺斯艾利斯。
哥德尔现在可以 формулировать 第三个定理:如果一个存在物 x 是神圣的,那么神性是它的本质属性。这是有道理的,因为如果某事物是神圣的,它就拥有所有正面特征——因此 x 的属性是固定的。
下一步关系到特定存在的存在。如果在某处至少存在一个存在物 y 具有属性 φ,而 φ 是 x 的本质属性,那么 x 也存在。也就是说,如果有什么东西是小狗般的,那么小狗也一定存在。
根据第五个公理,存在是一种正面属性。我认为大多数人都会同意这一点。
由此,人们现在可以得出结论,上帝存在,因为这个存在拥有每一个正面属性,而存在是正面的。
事实证明,哥德尔的逻辑推论都是正确的——甚至计算机也能够证明这一点。然而,这些推论也受到了批评。除了当然可以质疑的公理(为什么世界应该被划分为“善”和“恶”?)之外,哥德尔没有更详细地说明什么是正面属性。
确实,通过定义和公理,人们可以用数学方法描述集合 P
如果一个属性属于该集合,则其否定不包括在内。该集合是自包含的。
集合的本质仅具有集合的特征这一事实本身就是集合的一个元素。集合始终具有相同的元素——独立于情况。在这种情况下,情况是包含该集合的数学模型。
存在是集合的一部分。
如果 φ 是集合的一部分,那么将 φ 作为集合本质的属性也包含在集合中。
但是,所有这些都不能确保这个集合是唯一的。可能存在多个满足要求的集合。例如,正如逻辑学家所表明的那样,可以构建一些案例,在这些案例中,根据哥德尔的定义,存在超过 700 个本质不同的神圣实体。
这并不能解决一个(或多个)神圣存在最终存在的问题。数学是否真的是回答这个问题的正确方法本身就值得怀疑——即使思考它本身就非常令人兴奋。
本文最初发表于《Spektrum der Wissenschaft》,并经许可转载。
