想象一下你正在举办一个派对。你安排了零食,策划了播放列表,并在冰箱里放了各种啤酒。你的第一位客人来了,加入了一组六瓶装的啤酒,然后自己拿走了一瓶。你看着你的下一位客人到来,又贡献了几瓶啤酒,自己拿走了一瓶。准备喝一杯时,你打开冰箱,却惊讶地发现只剩下八瓶啤酒了。你并没有有意识地数啤酒,但你知道应该有更多,所以你开始四处寻找。果然,在保鲜抽屉里,在一颗腐烂的长叶莴苣后面,有几瓶啤酒。
你是如何知道要寻找丢失的啤酒的?你又不是站在冰箱旁守卫,统计有多少瓶啤酒进进出出。相反,你使用的是认知科学家所说的数字感,这是大脑中无意识地解决简单数学问题的一部分。当你在和客人热烈交谈时,你的数字感一直在记录冰箱里有多少啤酒。
长期以来,科学家、数学家和哲学家一直在争论这种数字感是与生俱来的还是后天习得的。柏拉图是西方传统中最早提出人类具有与生俱来的数学能力的人之一。在柏拉图的对话录《美诺篇》中,苏格拉底通过向一位没有受过教育的男孩提出一系列简单的问题,引导他领悟了勾股定理。苏格拉底的结论是,这个男孩一直都具有关于勾股定理的内在知识;提问只是帮助他表达出来。
支持科学新闻事业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和想法的有影响力的故事的未来。
在 17 世纪,约翰·洛克拒绝了这个观点,他坚持认为人类的心灵最初是一张白板,或者说是白纸一张,几乎所有的知识都是通过经验获得的。这种观点被称为经验主义,与柏拉图的天赋论形成对比,后来约翰·斯图尔特·密尔进一步发展了这种观点,他认为我们通过看到许多例子来学习二加三等于五,在这些例子中,这个等式成立:两个苹果加三个苹果等于五个苹果,两瓶啤酒加三瓶啤酒等于五瓶啤酒,等等。
简而言之,经验主义在哲学和心理学领域占据主导地位,直到 20 世纪下半叶,以诺姆·乔姆斯基为代表的倾向于天赋论的思想家将钟摆摆回了柏拉图的方向。乔姆斯基专注于语言,他提出儿童天生就具有一种内在的语言本能,这使他们能够在几乎没有明确指导的情况下快速习得他们的第一语言。
随后,其他人将乔姆斯基的假设扩展到数学领域。在 20 世纪 70 年代后期,认知科学家 C. R. Gallistel 和 Rochel Gelman 认为,儿童通过将他们语言中的数字词汇映射到一个人类与其他许多动物共有的、与生俱来的语言前计数系统上来学习计数。在他的里程碑式著作《数字感》(The Number Sense)中,该书于 1997 年首次出版,法国神经科学家 Stanislas Dehaene 提请人们注意支持这个语言前系统的汇聚证据,帮助来自不同学科——动物认知学、发展心理学、认知心理学、神经科学、教育学——的研究人员意识到他们都在研究同一件事。
在我们 2021 年发表在《行为与脑科学》(Behavioral and Brain Sciences)杂志上的论文中,我们认为,人类和许多非人类动物已经进化出处理数字的能力,这种观点不再有严肃的替代方案。柏拉图提出我们具有与生俱来的数学知识,或者说思考数字的能力,而我们认为我们具有与生俱来的数学感知——一种看到或感知数字的能力。当你打开冰箱时,并不是你看到了啤酒瓶,然后像你看到喜力啤酒的标签并推断出有人从荷兰带来了一款淡啤酒那样,对它们的数量做出推断。而是你看到了它们的数量,就像你感知它们的形状和颜色一样。
但并非所有人都同意这个观点,过去十年中,新一轮的经验主义已经兴起。那些拒绝先天数字感知能力存在性的批评者强调了一个更广泛且重要的科学挑战:我们如何才能知道婴儿或非人类动物头脑中的内容?作为认知科学哲学家,我们借鉴了数千年的哲学思考,并补充了大量的实验证据,而这些证据是过去的思想家根本无法获得的。
新兴证据
想象一下,你看到两个点集合在电脑屏幕上快速连续闪烁。没有时间去数它们,但如果你像成千上万做过这项练习的人一样,如果两者差异足够大,你就能分辨出哪个分组的点更多。虽然你可能很难区分 50 个点和 51 个点,但你很擅长识别 40 个点比 50 个点少。这种能力是与生俱来的,还是多年数学教育的产物?
2004 年,由 Dehaene 和 Pierre Pica 领导的一个法国研究小组将这个问题带到了巴西亚马逊地区深处。Pica 使用一台太阳能笔记本电脑,对来自与世隔绝的土著村庄的人们进行了相同的点闪实验。这个土著群体的人们也具有区分数量差异足够大的点的能力,即使他们接受的正式数学训练有限或根本没有,并且他们所说的语言中,精确的数字词汇最高不超过五。
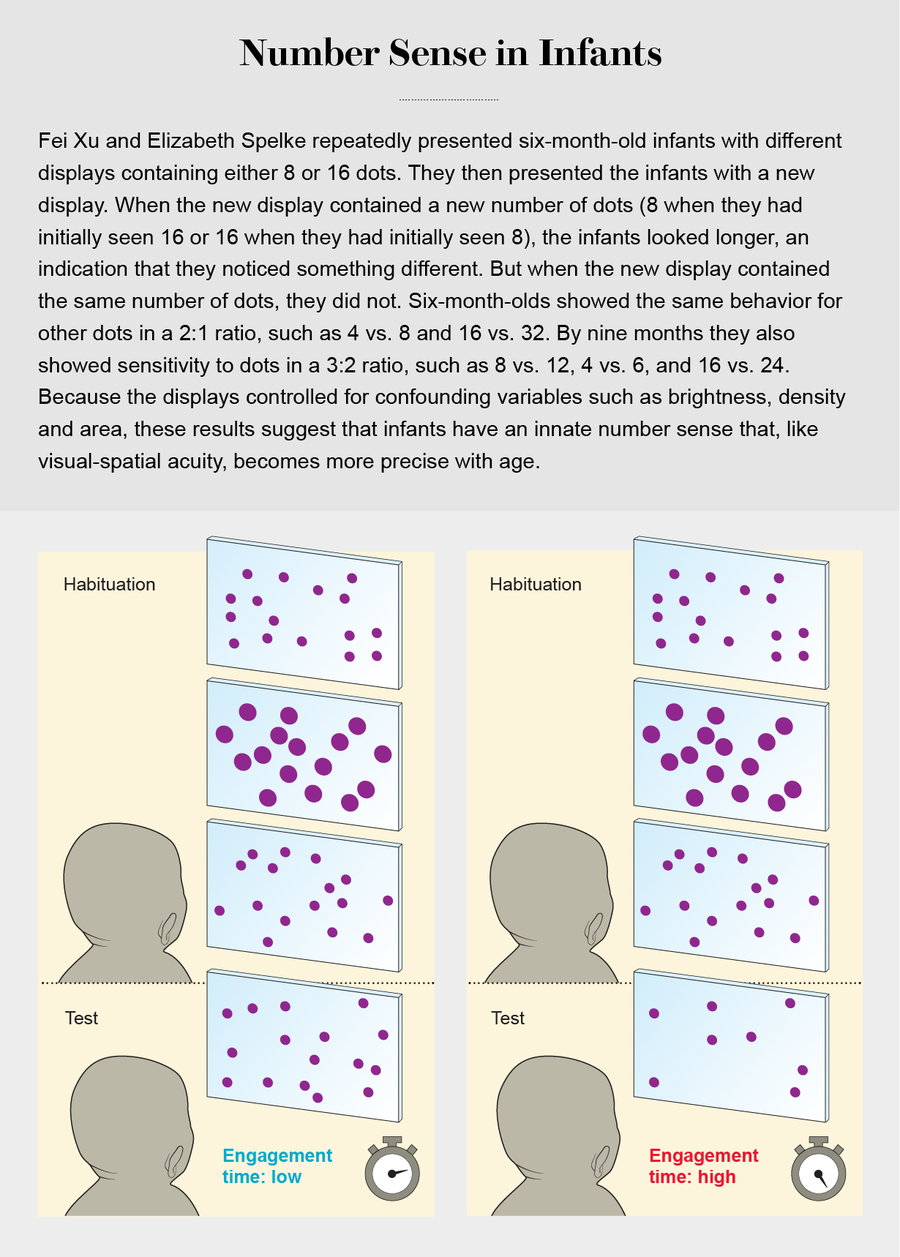
图片来源:Jen Christiansen;资料来源:Fei Xua 和 Elizabeth S. Spelke 在《认知》(Cognition)杂志,第 74 卷,2000 年 1 月发表的“6 个月大婴儿的大数辨别”(“Large Number Discrimination in 6-Month-Old Infants”)(参考)
大约在同一时间,包括发展心理学家 Elizabeth S. Spelke 和 Hilary Barth(当时都在哈佛大学)在内的另一个研究小组使用改进的点闪实验表明,马萨诸塞州的五岁儿童也具有这种能力。一种可能的解释是,孩子们实际上并没有追踪点的数量,而是专注于其他方面,例如点在屏幕上覆盖的总面积或簇的总周长。然而,当用快速连续的可听音调序列代替一个点集合时,孩子们同样很好地确定了哪个数量更大——也就是说,他们是听到更多的音调还是看到更多的点,就像在仅有点的实验中一样。孩子们不可能使用表面积或周长进行比较,因为音调不具有这些特征。点也不具有响度或音高。孩子们也没有使用声音持续时间:音调是按可变持续时间顺序呈现的,而点是一次性呈现固定持续时间的。看来,五岁儿童确实对点和音调的数量有一种感觉。
Barth 和她的同事继续表明,这些数字能力支持基本的算术形式。在另一个实验中,五岁儿童看到两组蓝点一个接一个地移动到一个不透明的方块后面。从那时起,就看不到任何蓝点了。然后,在方块旁边出现了一些红点。孩子们被问到是蓝点总数多还是红点总数多。他们回答正确,表明他们可以将两组蓝点加在一起,即使他们再也看不到它们了,然后将它们的总数与红点的总数进行比较。2021 年,Quuyan Qu 和她在宾夕法尼亚大学 Elizabeth Brannon 实验室的同事更进一步,表明年仅五岁的儿童就可以执行近似乘法——这种运算在美国三年级才开始教授。
人们很容易想知道,这些五岁儿童是否从他们的成年看护者那里学到了一些关于数字的知识,而他们的看护者在学校里学过数学。但是,在各种动物物种中也发现了类似的结果。狼在决定狩猎之前会考虑它们的群体规模,宁愿选择二到六只狼的群体去攻击麋鹿,但至少需要九只狼的群体才能对付野牛。老鼠学会按压杠杆一定的次数来换取食物。鸭子会考虑两个人分别向池塘里扔了多少食物,然后再决定接近谁。这种行为表明,数字感在进化上是很古老的,类似于看到颜色或感觉到温暖或寒冷的能力。
然而,这些例子并没有完全触及数字感是否是与生俱来的问题。也许它们只是表明,正规教育对于人类或动物学习计数来说不是必要的。测试与生俱来的数字感的理想对象是新生婴儿,因为他们没有时间学习太多东西。当然,他们不会说话,所以我们无法问他们两个集合中哪个包含更多。他们甚至不会爬行或伸手。然而,他们有能力进行一个更简单的动作:观看。通过测量婴儿观看的位置以及他们在那里凝视的时间,科学家们发现了通往他们思想的窗口。
在 2009 年 Spelke 与法国 Véronique Izard 和 Arlette Streri 领导的一个研究小组的合作中,巴黎一家医院的新生儿——所有婴儿都不到五天大——听了两分钟的听觉序列,其中包含四个声音(“嘟嘟嘟嘟”)或 12 个声音。然后,研究人员向婴儿展示了一个包含四个或 12 个物体的视觉显示。众所周知,婴儿喜欢看熟悉的东西,例如他们母亲的脸。Izard 和她的同事推断,如果婴儿从听觉刺激中提取数字,他们会更喜欢观看包含匹配数量项目的显示——在听到包含四个声音的序列后立即观看包含四个物体的显示,或在听到包含 12 个声音的序列后立即观看包含 12 个物体的显示。因此,当显示在数字上与声音匹配时,他们应该比不匹配时观看更长时间。
而这正是 Izard 和她的同事发现的。(正如微笑并不总是意味着同一件事一样,长时间观看也不一样:这里,新生儿在数字匹配时观看更长时间,表明巧合,而前一页方框中描述的六个月大的婴儿在数字变化时观看更长时间,反映出对意外的惊讶。在任何一种情况下,观看行为的可靠差异都表明婴儿对数字很敏感。)

图片来源:Jen Christiansen;资料来源:Hilary Barth 等人在《美国国家科学院院刊》(PNAS),第 102 卷,2005 年 9 月 19 日发表的“学龄前儿童的抽象数字和算术”(“Abstract Number and Arithmetic in Preschool Children”)(参考)
来自以色列海法大学的 Tali Leibovich-Raveh 和内盖夫本-古里安大学的 Avishai Henik 等批评者对过度解读这些结果提出了担忧,因为新生儿的视力很差。但事实上,在 16 名接受测试且没有入睡或烦躁的婴儿中,有 15 名婴儿都得到了这个结果,这无疑是具有启发性的。
数字与数码
回想一下我们的建议,即当你在派对上打开冰箱时,你看到有多少啤酒,就像你看到它们的形状和颜色一样。这不是不经思考的措辞:你没有看到啤酒瓶,然后再判断它们的数量。相反,数字感使你能够像看到颜色和形状一样看到数字。
为了澄清这个想法,首先重要的是区分数字和数码。数码是用于指代数字的符号。数码“7”和“VII”是不同的,但都指代同一个数字。你看到数字的说法不应与你看到数码的说法混淆。正如看到单词“红色”与看到红色颜色不同一样,看到数码“7”与看到数字七也不同。
此外,正如看到啤酒瓶的大小不涉及像“12 盎司”这样的符号出现在你的视野中一样,看到冰箱里有多少啤酒也不涉及看到像“7”这样的数码。当你看到啤酒瓶的大小,它看起来是某种样子——如果瓶子变大或变小,这种样子会改变。你可以通过观察来判断一个瓶子比另一个瓶子更大。相应地,当你看到有多少啤酒时,啤酒看起来是某种样子——如果啤酒更多或更少,这种样子会改变。因此,你可以仅通过观察来判断,是这里的啤酒多还是那里的啤酒多。

图片来源:Jen Christiansen;资料来源:David Burr 和 John Ross 在《当代生物学》(Current Biology)杂志,第 18 卷,2008 年发表的“视觉数字感”(“A Visual Sense of Number”)(参考)
当然,即使数字与数码区分开来,看到数字的概念可能仍然让人感到困惑。毕竟,数字是抽象的。你不能指着它们,因为它们不在空间中,而且你的眼睛肯定无法检测到任何从它们身上反射出来的光线。
但是,你看到数字的想法与你看到形状的想法并没有太大的不同。虽然你可以看到船帆是三角形的,但你不能单独看到纯粹的三角形,独立于任何物理物体。同样,虽然你可以看到一些啤酒大约是七瓶,但你不能单独看到数字七本身。你可以看到形状和数字,但只能作为物体或物体集合的属性,这些物体或物体集合将光线反射到你的眼睛中。
那么,我们如何判断某物是否被看到?如果你的新冠病毒检测中出现两条线,你可能会说你可以“看到”你感染了新冠病毒。但这只是一种随意的说法。你当然看到了这些线,但你只是判断你感染了新冠病毒。我们如何从科学角度来区分这种区别呢?
对于这个问题有很多答案,但其中一个最有帮助的答案是诉诸所谓的感知适应。一个例子是,当一个人在阳光明媚的日子去野餐时,他们的眼睛最终会适应阳光的方式。当这个人稍后回到室内时,即使所有的灯都亮着,浴室也会显得昏暗。在人的眼睛适应强光后,一个正常照明的房间看起来很暗。
适应是感知的一个标志。如果你可以感知到某物,你可能也可以适应它——包括它的亮度、颜色、方向、形状和运动。因此,如果数字是被感知的,人们也应该适应数字。这正是佛罗伦萨大学的视觉研究员 David Burr 和西澳大利亚大学的 John Ross 在 2008 年发表的一篇论文中报告的内容。
Burr 和 Ross 表明,如果一个人盯着大量的点阵列看,那么稍后包含中等数量点的阵列看起来会比原本的数量少。例如,他们发现,在一个人盯着 400 个点 30 秒后,他们看到一组 100 个点,就好像它只有 30 个点一样。因此,就像我们的眼睛会适应阳光一样,它们也会适应大量的数字,从而产生惊人的视觉效果。
包括斯沃斯莫尔学院的 Frank Durgin 在内的其他研究人员质疑,适应是否是数字的适应,而不是纹理密度的适应(项目在给定空间区域中出现的频率)。当点阵列的数量增加而它覆盖的面积保持不变时,它的纹理密度也会增加。但是,视觉科学家 Kevin DeSimone、Minjung Kim 和 Richard F. Murray 在 2020 年进行的一项研究中,将这些可能性区分开来,并表明观察者适应数字与纹理密度无关。尽管听起来很奇怪,但人类确实看到了数字。
天生的计数者
尽管有大量的证据,但当代的经验主义者——那些追随洛克和密尔的传统,并认为所有数学知识都是通过经验获得的的人——仍然对数字感的存在持怀疑态度。毕竟,算术能力传统上被认为是来之不易的文化成就。现在我们应该相信婴儿会做数学吗?
在过度解读非人类动物的数字能力方面,心理学家确实有着不良的历史记录。心理学专业的本科生会受到严厉警告,要提防“聪明的汉斯效应”,这个效应是以一匹马的名字命名的,这匹马曾被过早地认为具有精深的算术能力(更不用说辨别时间和用德语拼写长单词的能力)。后来揭示,它只是在对它的训练员行为中的细微线索做出反应。现在的研究人员非常注意避免无意中暗示他们的研究对象,但这并不能解决所有问题。
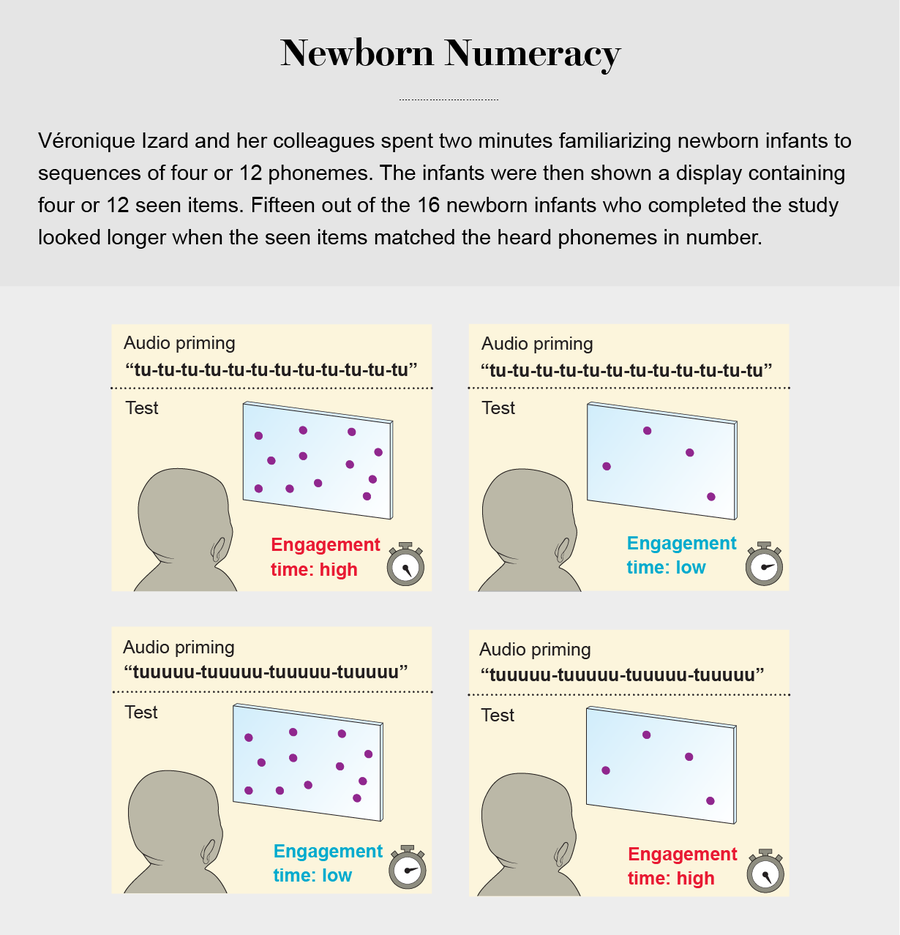
图片来源:Jen Christiansen;资料来源:Véronique Izard 等人在《美国国家科学院院刊》(PNAS),第 106 卷,2009 年 6 月 23 日发表的“新生儿感知抽象数字”(“Newborn Infants Perceive Abstract Numbers”)(参考)
例如,加州大学圣地亚哥分校的 Rafael Núñez 认为,数字感根本不可能代表数字,因为数字是精确的:30 比 29 正好多 1,比 31 正好少 1。相比之下,数字感是不精确的:如果你看到屏幕上闪烁 30 个点,你大概会知道有多少个点,但你不会知道确切地有 30 个点。Núñez 的结论是,无论数字感代表的是什么,它都不可能是数字。正如他在 2017 年发表在《认知科学趋势》(Trends in Cognitive Sciences)杂志上的一篇文章中所说,“涉及数字‘八’的基本能力应该要求将该数量视为与‘七’截然不同,而不仅仅是经常——或极有可能——被视为与‘七’不同。”
在我们 2021 年发表在《行为与脑科学》杂志上的文章中,我们回复说,这种担忧是 misplaced 的,因为任何数量都可以不精确地表示。你可以将某人的身高精确地表示为 1.9 米,但你也可以不精确地将其表示为接近两米。同样,你可以将你口袋里的硬币数量精确地表示为五个,但你也可以不精确地将其表示为几个。你分别代表的是身高和数字。所有改变的只是你如何表示这些数量——精确地或不精确地。因此,很难理解为什么数字感的不精确性应该被认为表明它代表的是数字以外的某些属性。
这似乎是一个语义问题,但它具有实质性的含义。如果我们像 Núñez 那样假设数字感不代表数字,那么我们需要说明它代表的是什么。似乎没有人对这个问题有任何好的想法。在许多关于数字感的研究中,其他变量——密度、面积、持续时间、高度、重量、体积、亮度等等——都得到了控制。
认为数字感与数字(而不是高度、重量、体积或其他数量)有关的另一个原因是来自 19 世纪后期的德国哲学家和逻辑学家哥特洛布·弗雷格。弗雷格在他的算术基础研究中指出,数字的独特之处在于它们预设了一种描述它们量化事物的方式。想象一下,你指着一副扑克牌并问:“有多少?”没有唯一的正确答案。我们首先需要决定我们是在数牌组的数量(一副),还是在数扑克牌的数量(52 张),即使这 52 张牌和这副牌是一回事。
弗雷格观察到,其他数量并非如此。如果我们想知道扑克牌有多重,我们把它们放在秤上,然后读出我们的答案。如果我们把它们看作是一副牌还是看作是一堆牌,它们的重量不会有任何差别。它们的体积也是如此。无论我们把扑克牌描述为一副牌还是 52 张牌,它们所占的空间量都是相同的。(当然,如果我们从牌组中取出一张牌,那么它的重量和体积将与整副牌不同。但那时我们改变的是我们所描述的东西,而不仅仅是如何描述它。)如果数字感对事物是如何描述的敏感,我们可以推测它真正代表的是数字,而不是其他数量。
当我们应用弗雷格的见解时,这正是我们发现的。西北大学 Steven Franconeri 领导的一个研究小组的工作给出了生动的例证。在 2009 年的一项研究中,他们向受试者展示了两个屏幕序列,屏幕上包含圆形和细线。与上述许多实验类似,受试者被问到哪个屏幕上的圆圈更多。他们也被告知完全忽略细线。但是,当线条恰好连接了两个圆圈,有效地将一对圆圈变成一个哑铃状物体时,受试者低估了屏幕上的圆圈数量。似乎他们忍不住将哑铃视为一个物体,即使他们试图忽略连接线,只关注圆圈。
观察者不仅仅是在追踪其他数量,例如物体的总表面积或屏幕上的像素总数。毕竟,两个圆圈和一条线是否连接成哑铃并不影响总表面积或像素数。它会影响的,而且似乎确实影响了的是显示器中感知到的项目数量。因此,正如将某物描述为一副扑克牌与描述为一堆单独的扑克牌会影响你如何计数它一样,你是否将某物在视觉上解释为一个哑铃还是一对圆圈,会影响你似乎看到的项目数量——这与弗雷格对追踪数字的视觉系统的预测完全一致。
这一切都不是否认数字感赋予的数学能力与大多数成年人拥有的成熟数学能力截然不同。如果你要求孩子们准确地拿出 15 颗软糖豆,只有学会用语言计数的孩子才能满足你的要求。但这并不是认为他们的数字感不代表数字的理由。正如孩子们在能够精确地思考距离之前很久就可以感知和辨别距离一样,他们在学会用语言计数和精确地思考数字之前就具有表示数字的能力。
就其本身而言,这些与生俱来的感知、加法、减法和数字运算的数学能力是有限的。但是,要理解婴儿是如何发展成为爱因斯坦的,我们绝不能低估婴儿最初对世界的把握。为了学习,我们需要一些实质性的东西来构建,而数字感为婴儿提供了新数字能力可以从中产生的基石的一部分——追踪硬币并创建货币经济的能力,发展现代数学的能力,或者更平凡地说,在冰箱后面找到那些丢失的啤酒的能力。

